Используя данные табл. 16.52 и таблицы координат исходных точек, вычислить уравненные значения дирекционных углов и расстояний (таблица уравненных значений дирекционных углов и расстояний подобна табл. 16.47).

Далее необходимо проверить качество уравнивания всех горизонтальных углов и расстояний по следующей схеме:

-вычислить разность уравненных дирекционных углов направлений, образующих угол ( αB1 – αBA = 117o23'40,4" – 251o08'14,3" = 226o15'26,1");

-вычислить уравненное значение угла, т.е. к измеренному значению

угла прибавить полученную в табл. 16.51 поправку (β1' = 226о15'25,0" + 1,1" = =226о15'26,1"); как видим, разница контрольного угла и уравненного его

значения получились одинаковыми в пределах погрешности округлений; - вычислить уравненное зачение расстояния как сумму измеренного рас-

стояния и поправки в него, полученной в табл. 16.51 (s1' = 475,8850 +0,0228 = =475,8824 м); из решения обратной геодезической задачи получено такое же значение (разности могут быть также в пределах округлений).

Указанные вычисления следует выполнить для всех измеренных и уравненных элементов. После контроля необходимо выполнить обработку полигонометрических ходов с использованием значений уравненных элементов.

155.5. Уравнивание направлений в триангуляции

Порядок уравнивания направлений в триангуляции параметрическим способом следующий.

1.Вычисляют предварительные значения координат определяемых пунктов и дирекционные углы сторон сети.

Здесь, с целью уменьшения влияния нелинейностей дифференцируемых функций, необходимо стремиться к тому, чтобы свободные члены уравнений поправок были как можно меньше по абсолютной величине. Этого можно достичь, если предварительно выполнить уравнивание углов в каждом из треугольников. Невязки в них следует распределить с обратным знаком поровну в каждый угол треугольника.

Из решения обратной геодезической задачи находят дирекционные углы

ирасстояния элементов сети. Предварительные координаты пунктов находят из решения прямых геодезических задач по длинам сторон и дирекционным углам. Значения расстояний находят по теореме синусов, а дирекционные углы – по кратчайшему пути от ближайшей исходной стороны. Если геодезическое построение позволяет использовать для вычисления координат формулы Юнга, то лучше воспользоватья такой возможностью.

2.Определяют коэффициенты a и b уравнений поправок, свободные члены l и составляют параметрические уравнения поправок.

470

Коэффициенты a и b находят по формулам (16.138) и (16.139), либо используют формулы

километрах. При таком выборе размерностей значения поправок в предварительные координаты получают в децимертах.

Коэффициенты a и b вычисляют с точностью до 0,001 при уравнивании

рующего угла в пункте k ; α ki0 - предварительное значение дирекционного угла указанного направления ; Mki – измеренное направление в пункте k на пункт i .

Контроль вычисления свободных членов производится по невязкам W по формуле

Невыполнение указанных условий не более 0,02" при вычислениях до 0,01" и не более 0,2" при вычислениях до 0,1".

Составляют уравнения поправок (16.143)

vki = − δ zk + aki ξ k + bkiη k − aki ξ i − bkiη i + lki

для всех направлений на данном пункте с учетом того (16.147), какой из пунктов исходный и определяемый.

Для упрощения выражений (16.143), уменьшения числа уравнений и исключения из них поправок ориентирования применяют правила Шрейбера.

Правило 1 (исключение поправок ориентирования).

Если одно из неизвестных в параметрических уравнениях поправок имеет коэффициент «минус единица», то для получения нормального уравнения, не содержащего этого неизвестного, его можно опустить в параметрических уравнениях поправок, добавив к ним сумму этих уравнений

(суммарное уравнение) с весом p = − 12n , где 1/2 – вес измеренного

направления, n – число данных направлений.

Пусть имеем несколько (n) уравнений

471

Поскольку на данном пункте должно выполняться условие (16.199), то последнее уравнение в системе уравнений (16.201) будет иметь вид

Правило 2.

Если в заданном ряду параметрических уравнений поправок имеются уравнения, различающиеся только свободными членами, то их можно заменить на одно уравнение.

Пусть

Это правило значительно упрощает дальнейшую вычислительную обработку.

Для приведения уравнения к весу, равному единице, необходимо умно-

В этом случае приведенные уравнения поправок (с весом, равным единице) имеют вид

472

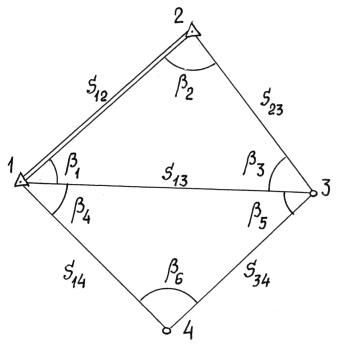
Рассмотрим принцип составления уравнений поправок для схемы триангуляции (рис. 16.14), состоящей из двух треугольников (10 направлений). Пункты 1 и 2 – исходные, пункты 3 и 4 – определяемые.

Рис. 16.14. Схема триангуляции

Составим уравнения поправок отдельно для каждого пункта, принимая, что погрешности исходных данных равны нулю: используются формулы (16.143) и (16.147).

Пункт 1 (исходный).

1. ν 12 = − δ z1 + l12

2. ν 13 = − δ z1 − a13ξ 3 − b13η 3 + l13

3. ν 14 = − δ z1 − a14ξ 4 − b14η 4 + l14

Пункт 2 (исходный).

4. ν 21 = − δ z2 + l21

(16.207)

Пункт 4 (определяемый).

9. ν 41 = − δ z4 + a41ξ 4 + b41η 4 + l41

10. ν 43 = − δ z4 + a43ξ 4 + b43η 4 − a43ξ 3 − b43η 3 + l43

Применим для уравнений (16.) 1-е правило Шрейбера, т.е. исключим неизвестное δzi , принимая во внимание условие (16.). Получим:

- пункт 1(исходный):

1.ν 12 = l12 ;...... p = 0,5

2.ν 13 = − a13ξ 3 − b13η 3 + l13 ;..... p = 0,5

473

- пункт 4 (определяемый):

12.ν 41 = a41ξ 4 + b41η 4 + l41 ;..... p = 0,5

13.ν 43 = a43ξ 4 + b43η 4 − a43ξ 3 − b43η 3 + l43 ;..... p = 0,5

14.ν å (4) = (a41 + a43 )ξ 4 + (b41 + b43 )η 4 - a43 ξ 3 - b43η 3 ;..... p = - 0,25

Уравнения 1 и 5 в системе уравнений (16.208) можно исключить, поскольку приведенные поправки являются известными. Кроме того, следует иметь в виду, что при преобразованиях изменяются значения поправок. В связи с этим нами условно приняты такие же обозначения в формулах (16.208), как и в формулах (16.207).

Далее сгруппируем уравнения для взаимообратных направлений и применим к ним 2-е правило Шрейбера. Примем также во внимание, что аik = - aki и bik = bki . Для удобства выполним такие преобразования, чтобы в общих формулах коэффициенты были положительными.

Направление 1-3(3-1):

474

Обратим внимание но то, что в системе (16.209) уравнения 3 и 6 можно объединить, используя 2-е правило Шрейбера. Т.е. вместо указанных уравнений записать объединенное -

После составления уравнений поправок в них подставляют вычисленные ранее коэффициенты и свободные члены, для упрощения вычислений все уравнения приводят к весу, равному ±1 (3-е правило) решают уравнения по установленным правилам и вычисляют поправки к предварительным координатам определяемых пунктов ( в рассматриваемом случае – к координатам пунктов 3 и 4).

Все вычисления, связанные с определением уравненных значений результатов измерений и контрольные вычисления выполняются по правилам, изложенным в § 154.

Далее в примере рассмотрено уравнивание направлений в сети триангуляции, состоящей из двух треугольников, в одном из которых имеется базисная (исходная) сторона, определяемая пунктами 1 и 2 (рис. 16.14).

Координаты пунктов 1 и 2:

Х1 = 5364,756 м; Y1 = 4256,214 м; Х2 = 8836,421 м; Y2 = 5748,265 м.

Исходный дирекционный угол α12 = 23о15'25,38", длина исходной стороны (базиса) S12 = 3778,7133 м (из решения обратной геодезической задачи).

В данном геодезическом построении измерены направления в каждом из пунктов (всего 10 направлений) и вычислены углы βi (табл. 16.53).

Все вычисления в примерах будем выполнять на порядок выше, а округлять затем только уравненные величины.

Предварительно выполним следующую обработку в схеме триангуляции: по теореме синусов найдем стороны S23, S14 и S43; вычислим дирекционные углы направлений 2-3, 1-4 и 4-3 через известный дирекционный угол направления 1-2 и вычисленные значения углов: определим предварительные координаты точек 3 и 4 по ходу 1-2-3-4-1-2 и выполним предварительное уравнивание координат (табл. 16.54); по полученным данным из решения

475

обратной геодезической задачи найдем дирекционные углы определяемых сторон сети.

Пользуясь табл. 16.54, вычислим по формулам (16.194) значения коэффициентов уравнений поправок (табл. 16.55).

Вычислим по формуле (16.196) значения ориентирующих углов в пунктах:

Незначительные отступления от условия (16.199) объясняются погрешностями округлений.

476

После подстановки значений коэффициентов a и b и свободных членов l в уравнения (16.209) с учетом преобразований значений свободных членов при объединениях уравнений по правилам Шрейбера получим:

единице». Для этого умножим коэффициенты и свободные члены этих уравнений на р . Получим

Составим по уравнениям (16.211) матрицу коэффициентов, свободных членов и весов для получения нормальных уравнений поправок (табл. 16.57).

В соответствии с правилами составления нормальных уравнений получим:

1. 10,992 ξ 3 + 2,334η 3 − 0,954 ξ 4 − 2,309η 4 − 0,959 = 0 2. 2,334 ξ 3 + 5,457η 3 + 1,863ξ 4 − 3,933η 4 − 0,867 = 0

477