Деление горизонта на 32 румба впервые применили итальянцы еще в начале XIV века. Ранее величина румба составляла 11,25о. Затем румбом стали называть любой острый угол, определяемый направлением линии и ближайшим к ней направлением меридиана с обязательным указанием двух основных сторон света.

Румбовая (четвертная) система может быть использована для любого из рассмотренных выше ориентирующих углов, в зависимости от меридиана, взятого в качестве исходного для ориентирования направления. В общем случае ориентирующий угол А (АИ, АМ, α) взаимосвязан со значением румба соотношениями, приведенными в табл. 2.5 (рис. 2.19).

§ 18. Решение некоторых задач с использованием топографической карты

18.1. Измерение расстояний

Использование численного, именованного и линейного масштабов. Положение любой точки земной поверхности на плоскости получается в результате проецирования ее по определенным математическим законам на вспомогательную поверхность референц-эллипсоида и последующего построения плоского изображения в проекции Гаусса-Крюгера. При построении топографических планов выполняют ортогональное проецирование точек на горизонтальную плоскость. Очевидно, что расстояние между двумя точками, пройденное на местности, в общем случае отличается от его проекции на горизонтальную плоскость. Поэтому на картах и планах измеряют не фактическое расстояние, а т.н. горизонтальное проложение, которое является проекцией линии местности на горизонтальную плоскость. При этом принято величину измеренного на карте отрезка называть расстоянием.

При измерении расстояний на топографических картах или планах используют различные виды масштабов. В § 6 были рассмотрены численный и именованный масштабы (напомним: численный масштаб 1:5000, соответствующий ему именованный масштаб – «в 1 см 50 м»). Под численным и именованным масштабами, записанными под южной рамкой карты, располагают линейный масштаб.

Линейный масштаб (рис. 2.20) – это графическое изображение численного или именованного масштабов. Отрезок а линейного масштаба называют

46

основанием. Первое основание делят на отрезки величиной 1 мм, что обеспечивает графическую точность отсчета до 0,1 мм.

Рис. 2.20. Линейный масштаб.

Пример 2.10. На карте масштаба 1:25000 измерено расстояние, которое получилось равным 36,7 мм.

Определить расстояние на местности.

Решение.

При использовании численного масштаба соответствующее расстояние на местности будет равно 36,7 мм х 25000 = 917500 мм = 917,5 м.

При использовании именованного масштаба (в 1 см 250 м) отрезок 36,7 мм = 3,67 см на местности будет соответствовать отрезку 3,67 см х 250 = 917,5 м.

При использовании линейного масштаба величину измеряемого отрезка необходимо взять в раствор циркуля-измерителя и перенести его на шкалу линейного масштаба. Искомый отрезок будет определен непосредственно по линейному масштабу.

Следует заметить, что при использовании численного и именованного масштабов получается одинаковый ответ, а при использовании линейного масштаба полученная величина может несколько отличаться от вычисленной из-за графических погрешностей, возникающих при использовании измерителя и при отсчете по шкале линейного масштаба, а также из-за возможной деформации листа топографической карты. В последнем случае использование линейного масштаба является предпочтительным, поскольку при использовании численного или именованного масштабов иногда бывает необходимо определять коэффициент деформации и вводить его значение в результат измерения.

Использование поперечного масштаба. Для точного нанесения точек на топографические план и карту, а также при построении на карте и плане точек по их координатам, используют поперечный масштаб.

Поперечный масштаб (рис. 2.21) представляет собой особую графическую шкалу (номограмму), основанием которой служит линейный масштаб. Линейный масштаб достраивают вертикальной шкалой с разбивкой ее, например, так же, как и основания, на 10 частей по вертикальному направлению. Наклонными линиями (трансверсалями) соединяют нижние деления с верхними.

Число делений n горизонтального отрезка шкалы поперечного масштаба и число делений m вертикального отрезка может быть различным. При n = m = 10 поперечный масштаб называют нормальным или сотенным. Основание а нормального поперечного масштаба чаще всего делают равным 2 см. В соответствии с этим, цена деления меньшего отрезка основания будет

47

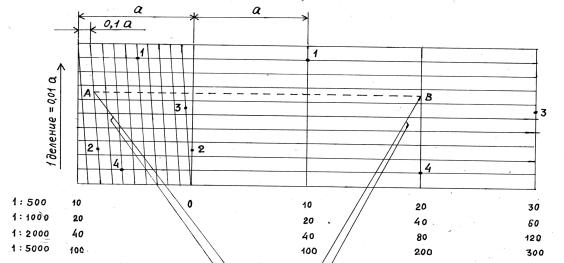
равна 2 см : 10 = 0,2 см = 2 мм. При перемещении вверх (вниз) по трансверсали на один шаг соответствующий горизонтальный отрезок увеличится (уменьшится) на величину 0,2 см : 10 = 0,02 см = 0,2 мм или на величину (а : 100). Таким образом, перемещение на один шаг по трансверсали составит 1:100 основания.

Рис. 2.21. Поперечный масштаб.

Пример 2.11. Необходимо определить длину отрезка АВ, взятого в раствор измерителя с планов различных масштабов.

Решение.

На рис. 2.21 приведена оцифровка основания поперечного масштаба в соответствии с используемым масштабом плана и величины наименьших отрезков основания и трансверсали.

Обратите внимание на то, что отрезки АВ, 2-2, 3-3 располагаются на трансверсали между горизонтальными линиями, что дает возможность точнее определить их длину.

Для масштаба 1:500 отрезок АВ можно представить в виде следующего набора: два полных основания (20 м), плюс восемь полных делений основания (8 м), плюс шесть с половиной делений по трансверсали (0,65 м) = 28,65 м.

Для масштаба 1:2000 АВ = 2 х 40 м + 8 х 4 м + 6,5 х 0,4 м = (80 + 32 + 2,6) = 114,6 м. Определите значения отрезка АВ для других масштабов.

Пример 2.12. Отложить на поперечном масштабе отрезок L заданной длины в масштабе соответствующего плана.

Решение: приведено на рис. 2.21.

Построение отрезка 1-1 длиной 14,9 м в масштабе 1:500 (основание равно 10 м): отрезок содержит одно полное основание (10 м); остаток 14,9 – 10,0 = 4,9 м содержит четыре полных деления основания (4 м); остаток 4,9 – 4,0 = 0,9 м содержит девять делений (переходов) по трансверсали.

Построение отрезка 2-2 длиной 16,5 м в масштабе 1:1000 (основание равно 20 м): отрезок меньше основания, поэтому один его конец будет находиться на нулевой вертикальной линии; в длине отрезка содержится восемь полных делений основания (16 м); остаток 16,5 – 16,0 = 0,5 м соответствует перемещению по трансверсали вверх на два с половиной деления (в одном делении по трансверсали 0,2 м).

Аналогичным образом построены отрезки 3-3 (305,5 м в масштабе 1:5000) и 4-4 (104,4 м в масштабе 1:2000). Проверьте результаты построения и потренируйтесь в решении подобных задач.

48

18.2. Определение географических и прямоугольных координат

Определение географических координат. Лист топографической карты ограничен по долготе меридианами и широте параллелями, географические координаты которых определяются по схемам разграфки карт при образовании их номенклатуры (см. § 10). Таким образом, точки или объекты местности, изображенные на листе топографической карты, имеют географические координаты в пределах разности долгот λ = (λВ – λЗ) и разности широт φ = (φС – φЮ). Здесь индексы В, З, С, Ю относятся к восточной, западной, северной и южной рамкам карты.

Для удобства в определении географических координат и повышения точности разности долгот и широт разделены на минутные метки (рис. 2.22), которые, в свою очередь, точками поделены на 6 интервалов по десять секунд в каждом из них.

Рис. 2.22. Определение по карте географических и прямоугольных координат.

Определение географических координат т. А заключается в построении через нее параллели и меридиана. Полученные географические координаты этих линий и будут определять географические координаты искомой точки.

49

Построение параллели и меридиана выполняется с помощью большой линейки с ровным краем, перекрывающей внешнюю рамку карты. Линейку необходимо установить так, чтобы ее ребро проходило через т. А и через одинаковые отсчеты широты (долготы) на соответствующих минутных метках.

Для топографических карт малых и средних широт, представляющих собой практически прямоугольник, для определения широты или долготы можно воспользоваться треугольником с прямым углом. В этом случае проектирование точки А на шкалы широт и долгот производится по перпендикуляру к рамке карты. Таким образом, долгота точки А λА = 22º31'11" (восточная), широта φА = 54º35'26" (северная).

Можно решить и обратную задачу: нанести на карту точку по ее географическим координатам. Для этого с помощью большой линейки необходимо построить меридиан с долготой, равной долготе точки, и параллель с широтой, равной широте точки. На пересечении графически полученных меридиана и параллели будет находиться искомая точка.

Определение прямоугольных координат. Сетка прямоугольных координат на топографической карте строится в виде квадратов, стороны которых параллельны оси х прямоугольной системы координат и перпендикулярны оси у. В зависимости от масштаба карты подписи километровых линий производятся через определенный шаг, выраженный в километрах.

Например, для карт масштабов 1:10000, 1:25000 и 1:50000 этот шаг равен 1 км, для карты масштаба 1:100000 – 2 км. Километровые линии подписывают на внешней рамке карты (рис. 2.22) двумя последними цифрами километров. Полные координаты х и у подписывают только у крайних на листе карты километровых линий.

Сокращенными координатами точки называют квадрат, в котором она находится. Обозначение квадрата складывается из значения горизонтальной и вертикальной линий километровой сетки для юго-западного его угла. Так, точка А находится в квадрате 5311, точка В – в квадрате 5211,точка С – в квадрате 5410, точка D – в квадрате 5112.

Определение прямоугольных координат т. В сводится к измерению отрезка а по оси х и отрезка b по оси у. Величину отрезка можно определить любым из способов, рассмотренных в разделе 18.1.

В некоторых случаях точка может находиться в неполном квадрате – точки С и D. В рассматриваемом случае координата х точки С определяется так же, как и соответствующая координата т. В. Для определения координаты уС необходимо измерить отрезок b´ и вычесть его из координаты линии 4811 км. Для точки D координата уD определяется сложением координаты 4812 км и отрезка b , а для определения координаты хD необходимо измерить отрезок а´ и вычесть его из координаты 6052 км.

В табл. 2.6 представлен пример определения координат точек С и D. Здесь также можно решить и обратную задачу: нанести точку на карту

(план) по ее прямоугольным координатам. Для этого необходимо определить квадрат, в котором находится данная точка, а затем, пользуясь измерителем и

50