27) Предел показ-степенной ф-ии. Непрерывная ф-ия.

y = f(x), x₀  D(f) Функция f(x), определенная в некоторой окрестности точки х₀, называется непрерывной в этой точке, если предел функции в точке x₀ существует и равен значению в этой точке: lim f(x) = f(x₀)

28. Односторонняя непрерывность. Точки разрыва и их классификация. Точка x=x₀ называется точкой разрыва функции y=f(x), если эта функция не является непрерывной в этой точке. Точка x=x₀ называется точкой разрыва первого рода, если в этой точке существует предел слева и справа от этой функции. Точка x=x₀ называется точкой разрыва второго рода, если хотя бы один из пределов слева и справа не существует.

Одностр.непрер. В определении непрер.ф-ии в точке x₀ требуется существование и неравенство. С применением односторонних пределов определ.понятие непрерывности ф-ции в точке слева и справа: Ф-ия наз-ся непрер.в точке х0 слева, если: ∋f(x0-0)= f(x)=f(x0). Ф-ия f(x) наз-ся непрер.в рочке х0 справа, если: : ∋f(x0+0)= 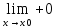f(x)=f(x0)

29. Св-ва ф-ции непрерывной на отрезке а;б 1) Сохранение знака. 2)Первая и вторая теорема Больцмана-Коши. 3) Ограниченность ф-ции.1 и 2 теоремы Вейерштрасса. Теорема об обратной ф-ции.

Сохранения знака: Если f(x) непр. в т-ке х0 и f(x0)0 то  окрестность этой т-ки в которой ф-ция принимает тот же знак что и знак х0.

Непрер.на отрезке.

Пусть теперь [a;b] (замкнутый) отрезок в D(f) . Назовём функциюf(x) непрерывной на отрезке[a;b] , если f непрерывна на интервале (a;b) , непрерывна справа в точке a и непрерывна слева в точке b , то есть 1) ∀x₀∈(a;b)∋ 2) ∋ 3) .

Теорема Вейерштрасса. Из любой огран.послед.можно выделить сходящиеся подпослед. 1) {x_n} безчисл.мн-во одинаковых членов 2) {x_n} имеется безчисл.мн-во разл.членов. 1) хотя бы один из членов {x_n}повтор.безчисл.кол-во раз. x_n1=x_n2=…=x_nk-сход.послед.

30. Понятие равномерной непрерывности. Функция f (x) называется равномерно-непрерывной на данном множестве, если для всякого ? > 0 можно найти такое ? = ?(?) > 0, что |f (x1) — f (x2)|x1 и x2 из данного множества, удовлетворяющей условию |x1—x2|< ? (ср. Непрерывная функция). Например, функция f (x) = x2 равномерно непрерывна на отрезке , равномерно непрерывна на этом отрезке (теорема Кантора). Для интервала эта теорема может не иметь места.

31) Комплексные чи́сла[ — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица, то есть число, удовлетворяющее уравнению i2 = − 1.

Действия над комплексными числами.

Сравнение

a + bi = c + di означает, что a = c и b = d.

Сложение

(a + bi) + (c + di) = (a + c) + (b + d)i

Вычитание

(a + bi) − (c + di) = (a − c) + (b − d)i

Умножение

(a + bi)(c + di) = ac + bci + adi + bdi2 = (ac − bd) + (bc + ad)i

Деление

(a+bi)/(c+di)=(ac+bd)/(c²+d²)+((bc-ad)/(c²+d²))i

32) Определение производной. Производной фкц. Y=f(x) называется предел отношении приращения фкц к приращению аргумента при условии что приращение аргумента стремится к 0, если этот предел существует.

33) Механически и геометрически смысл производной y’. Пусть точка m движется не равномерно прямолинейно по некоторому пути и к моменту t+∆t проидет путь S+∆S ; Uср= ∆S/∆t. О1. Скоростью точки в мом времени t называется предел котор стремиться ср скорость за промежуток ∆t при условии что ∆t стремится к 0. (мгновенная скорость точки в момент времени Х).Геом смысл доказывает существование предельного значения (при ∆х→0) угла наклона секущей.

34) Основные элемент.ф-ии. Степенные функции: y = x^a,

где а – любое постоянное число. Областью определения считается промежуток x > 0, но если, например, а–натуральное число, функция определена для всех х.1) Показательная функция: y = a^x, где a > 0, a ≠1. Область определения – множество всех действительных чисел. 2) Логарифмическая функция: y = log_ax, где a > 0, a ≠1. Область определения: x > 0. 3) Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x. Область определения для sin x и cos x – множество действительных чисел. 4) Обратные тригонометрические функции: y = arcsin x, y = arccos x, y = arctgx. Область определения x  -1; 1 для arcsin x и arccos x, множество действительных чисел для arctg x. Элементарные функции непрерывны в каждой точке своей области определения. 35)Правило вычисления производных.1.[cf(x)]’=c*f’(x);2[f(x)±g(x)]’=f(x)±g(x);3 [f(x)*g(x)]’=f’(x)*g(x)+f(x)*g’(x); 4. [f(x)/g(x)]’=f’(x)g(x)-f(x)g’(x)/g²(x); 5.[f(g(x))]’=f’(g(x))*g’(x);6.[f^(-1)(x)]= 1/f’(f^9-1)(x)) .

36) Дифференцируемые ф-ии. Функция y=f(x) назыв дифференцируемой в данной точке х, если преращение ▲у этой фкц в точке х, соотв преращ аргумента ∆х, может быть представлено в виде ∆у=А∆х+α∆х, где А это некоторое число , независ от ∆х, а α – это фкц аргумента∆х, явл бескон малой при ∆х→0.

37) Дифференциал. В случае А/0 диф-лом ф-ии у=F(x) в данной точке х, соответствующим приращению аргумента ∆х, называют главную линейную относительно ∆х часть приращения этой ф-ии в точке х. в случае А=0 то слогаемое А∆х перестает быть главной частью приращения ∆у диференц ф-ии.