
- •1) Бином Ньютона. Теорема паскаля.
- •2)Множества. Спосмобы задания. Точные границы.
- •3. Отрезок, интервал, ∈-окрестность, проколотая окрестность. Ограниченные и неограниченные множества.
- •4) 1.Абсолютная величина. Свойства:
- •5)Определение функции. Способы задания. Сложная функция, обратная функция. Основные элементарные функции.
- •6) Числовые последовательности. Придел числ.Послед.
- •14) Полпоследовательности. Теорема Больцана-Вейерштрасса.
- •15) Предельная точка области определения функции. Предел функции в точке (определения по Коши и Гейне). Эквивал. О.1 и о.2.
- •16) Теорема о пределах ф-ии.
- •18) Необходимые и достаточные условия сущ-ия предела ф-ии.
- •27) Предел показ-степенной ф-ии. Непрерывная ф-ия.
- •39) Производные и диффернциалы высших порядков.
- •42. Исследование функции методом дифференциального исчисления. 1)Производная сложения функции. Теорема. Формyла Лейбница. 2)Вывод производных
14) Полпоследовательности. Теорема Больцана-Вейерштрасса.
Пусть дано {xn} некоторая посл-ть и nk – некоторая строго возраст.посл-ть состоящ.из натур.чисел, посл-ть {xn} наз-ся подпоследовательностью данной посл-ти {xn}. Пусть {xn}. Может предела не иметь, а посл-ть {xnk} имеет предел: {xn}= {(-1)n}={-1,1,-1,1…}. nk={xnk}= {1,1….1}. n=2k.
Теорема Больц-Вейерштрасса. Из всякой огран.посл-ти {xn} можно выбрать сходщуюся подпос-ть. а<xn<b, ∀n∈N. Возьмем отрезок [a;b] и разделим пополам,тогда в одной из половинок находится бесконечно много элементов посл-ти. [a;b]⊃[a1;b1]⊃[a2;b2]⊃…
bk-ak=b-a/2k,
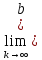 k
–ak)=0.
Это
означает, что пос-ть вложенных отрезков
стягиваются и все они имеют одну общую
точку С.
k
–ak)=0.
Это
означает, что пос-ть вложенных отрезков
стягиваются и все они имеют одну общую
точку С.
15) Предельная точка области определения функции. Предел функции в точке (определения по Коши и Гейне). Эквивал. О.1 и о.2.
Предел ф-ии в точке. Мн-во, на катором определена ф-ия, может быть любым. Точка а, предел которой мы рассматриваем, должна быть предельной точкой этого мн-ва, предельной точкой этого мн-ва, т.е. любой ее, достаточно малой окрестности должно содержаться бесконечно много точек мн-ва.
По
Коши: А= δ(a)=>f(x)∈Uε(A).
δ(a)=>f(x)∈Uε(A).
По
Гейне.
 n=a,
{xn},
xn≠a,
f(xn).
Если
для любой сходящ.к а посл-ти {xn}
такой,что х≠а, соотв.посл-ть значений
ф-ий f(xn)
сходится к одному и тому же числу А, то
число А наз-ся пределом ф-ии при х→а.
n=a,
{xn},
xn≠a,
f(xn).
Если
для любой сходящ.к а посл-ти {xn}
такой,что х≠а, соотв.посл-ть значений
ф-ий f(xn)
сходится к одному и тому же числу А, то
число А наз-ся пределом ф-ии при х→а.
16) Теорема о пределах ф-ии.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) Ј z(x) Ј v(x), и limx® a u(x)=limx® a v(x)=b, то limx® a z(x)=b. ("Теорема о двух милиционерах").
17) Односторонние пределы. Gредел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (или пределом справа).
Пусть задана числовая функция f : M⊂R→R и a ∈ M — предельная точка области определения M.
Число A ∈R называется правосторонним пределом функции f при x стремящемся к a, если
∀ε>0∃δ>0 ∀x∈(a,a+δ)∩M lf(x)-Al<ε.
Число называется левосторонним пределом функции f при x стремящемся к a, если
∀ε>0∃δ>0 ∀x∈(a-δ,a)∩M lf(x)-Al<ε.
18) Необходимые и достаточные условия сущ-ия предела ф-ии.
Необходимость.
A=
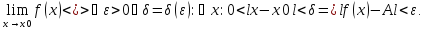
Достаточность.

19)
Первый замечательный предел.Следствия.
 –
первый замечательный предел. Следствия.
1)
–
первый замечательный предел. Следствия.
1)
 2=1/2.
2)
2=1/2.
2)
 .
.
3)
 .
3)
.
3) .
4)
.
4)
20) Предел ф-ии при х→∞. при х →∞ (случаи когда х0 есть +∞ или -∞). А именно, равенство (*) во всех случаях означает следующее: для любой последовательности { хn}, сходящейся к х0 , соответствующая последовательность {f(хn)} сходится к а
21)
Второй замечательный предел. Следствия.
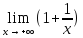 x=e.
Следствия:
x=e.
Следствия:
1)
 x=e.
2)
x=e.
2)
 1/x=e.
3)
1/x=e.
3)
 =.
4)
=.
4)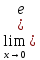 x-1)/x
– 1. 5)
x-1)/x
– 1. 5)
 x-1)/x
= lna
x-1)/x
= lna
22) Сравнение б.м.ф-ий. Применения для вычисления предела.
Пусть
α(x)
и β(x)
— две функции, бесконечно малые в точке
x=a.
Если
 , то говорят, что α(x)
более высокого порядка малости, чем
β(x)
и обозначают α(x)=0(β(x))
. Если же
, то говорят, что α(x)
более высокого порядка малости, чем
β(x)
и обозначают α(x)=0(β(x))
. Если же , тоβ(x)
более высокого порядка малости, чем
α(x);
обозначают β(x)=0(α(x)).
Бесконечно малые функции α(x)и
β(x)
называются бесконечно малыми одного
порядка малости, если
, тоβ(x)
более высокого порядка малости, чем
α(x);
обозначают β(x)=0(α(x)).
Бесконечно малые функции α(x)и
β(x)
называются бесконечно малыми одного
порядка малости, если
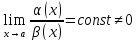 , обозначают α(x)=0(
, обозначают α(x)=0( .
И, наконец, если
.
И, наконец, если не существует, то бесконечно малые
функции α(x)
и β(x)
несравнимы.
не существует, то бесконечно малые
функции α(x)
и β(x)
несравнимы.
Если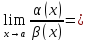 , то бесконечно малые функции α(x)
и β(x)
называются эквивалентными, обозначают
α(x)~β(x).
, то бесконечно малые функции α(x)
и β(x)
называются эквивалентными, обозначают
α(x)~β(x).
23)
Непрерывность ф-ии. Функция
f(x) называется непрерывной в точке x=x0,
если ее предел в этой точке равен значению
функции в этой точке. Условия
непрерывности:1)х0∈D(f)
2)∃ 3)
3) ∀ε>0,∃δ>0:lx-x0l<δ=>lf(x)-f(x0)l<ε.
Функция y=f(x) называется непрерывной в
точке x=x0,
если она определена в некоторой
окрестности точки x0
(очевидно,
и в самой точке x0)и
если
∀ε>0,∃δ>0:lx-x0l<δ=>lf(x)-f(x0)l<ε.
Функция y=f(x) называется непрерывной в
точке x=x0,
если она определена в некоторой
окрестности точки x0
(очевидно,
и в самой точке x0)и
если
 или,что то же самое
или,что то же самое Функция y=f(x) называется непрерывной на
данном промежутке, если она непрерывна
в каждой точке этого промежутка.
Функция y=f(x) называется непрерывной на
данном промежутке, если она непрерывна
в каждой точке этого промежутка.
24. Непрерывность сложной функции.
y=f(𝛗(t)), φ(t = x.
Теорема.
1)Если ф-ия φ(t) непрер.в точке t0
2)Ф-ия f(x) непрер.в т. x=x0
Причем φ(t0)=x0.=> то y = f(φ(t))- непрер.в точке t=t0
25) Арифм.оперции над непрерывными ф-ми. Теорема. Пусть ф-ии f(x) и g(x) определены в области Д и непрерывны в точке х0 пранадлежащей области Д, тогда в этой точке неррерывны f(x)±g(x), g(x)*f(x), f(x)/g(x) при условии что g(x0)≠0.
26) Непрерывные элементарные ф-ии.Пример. Ф-ии, которые получаются из осоновных, с помощью конечного числа арифметическимх операций, а так же конечного числа суперпозиции наз-ся элементарными функциями.
