2.ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

2.1. Основные понятия

Основные понятия теории функций нескольких переменных по своей сути не отличаются от соответствующих представлений теории функций одной переменной. Это, естественно, не означает, что все результаты, полученные для функций одной переменной, можно механически переносить на случай функций двух и более переменных. Необходимы определенные обобщения и осторожность в интерпретации результатов.

Начнем с простейших обобщений.

Расстояние между точками.

1)Чтобы описать положение точки P на числовой оси Ox , достаточно указать единственное число: x −координату точки. Расстояние между точками P( x) и P0 (x0 ) числовой прямой определяется формулой

ρ(P, P0 ) =| x − x0 |= (x − x0 )2 .

2)Любая точка P координатной плоскости xOy описывается упорядоченной парой вещественных чисел ( x, y) , а расстояние между точками P(x, y) и P0 (x0 , y0 ) этой плоскости вычисляется по формуле

понятие геометрический смысл. В этом же смысле используется термин “точка n -мерного пространства”, т.е. в смысле “упорядоченная совокупность чисел ( x1, x2 ,..., xn )”. Расстояние между точками P(x1, x2 ,..., xn )

и P(a1,a2 ,...,an ) n -мерного пространства определяется формулой

что является естественным обобщением привычного понятия “расстояние”.

Определение функции

Если каждой точке P(x1, x2 ,..., xn ) некоторой области D n -мерного

пространства поставлено в соответствие значение переменной u , то говорят, что в области D задана функция u переменных x1, x2 ,..., xn :

u = f (x1, x2 ,..., xn ) .

Область D называется областью определения функции.

17

Общеупотребительным является и более короткое обозначение: u = f (P) .

Функцию двух переменных обычно обозначают в виде z = f (x, y) .

Уравнение z = f (x, y) при этом можно интерпретировать как уравнение поверхности в обычном трехмерном пространстве, а областью определения функции f (x, y) является проекция этой поверхности на координатную плоскость xOy .

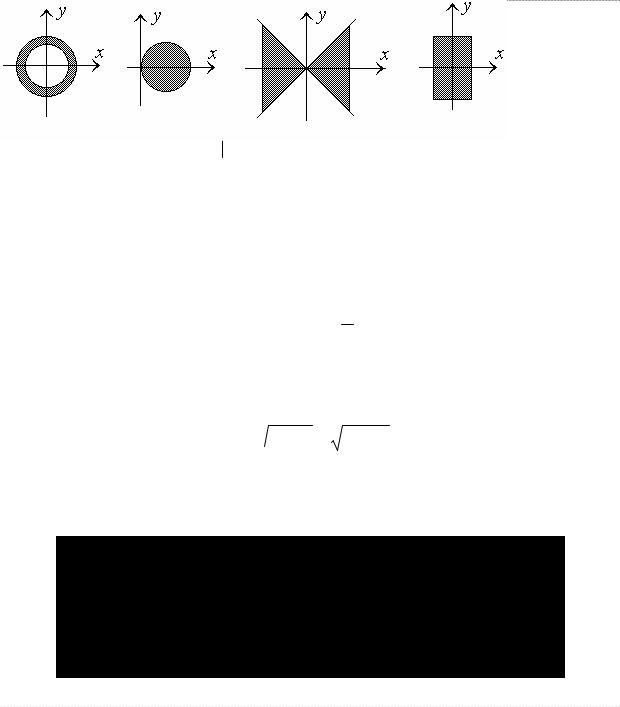
Пример 1. Областью определения D функции

z = x2 + y2 −1 + 2 − x2 − y2

является кольцо с центром в начале координат: 1 ≤ x2 + y2 ≤ 2 .

Используя символику теории множеств, можно записать, что

D ={x (x2 + y2 ≥1) I(x2 + y2 ≤ 2)}.

Пример 2. Областью определения функции

z = ln(2x −x2 −y2 )

является внутренняя часть круга радиусом 1 с центром в точке P0 (1,0) : (x −1)2 + y2 <1.

Пример 3. Область определения функции z = arcsin xy

определяется неравенствами

| y |≤| x | , x ≠ 0 .

Пример 4. Областью определения функции

z = 1 − x2 + 4 − y2

является прямоугольник:

| x |≤1, | y |≤ 2

Области, рассмотренные в Примерах 1-4, показаны схематически на Рис. 1.

Рис. 1

18

2.2.Пределы

Напомним, что в случае функции одной переменной математическое утверждение

lim f (x) = A

x→a

означает, что значения функции f ( x) становятся сколь угодно близкими к

числу A - по мере того, как расстояние между точками x и a стремится к нулю.

Предел функции нескольких независимых переменных имеет в точности такой же смысл, а само понятие предела функций нескольких переменных вводится совершенно аналогично тому, как это делается для функции одной переменной.

Пусть функция f (P) (любого числа переменных) определена в некоторой окрестности точки P0 .

Тогда число A называется пределом функции f (P) при P → P0 ,

используются и другие формы записи. Так, в случае функции двух переменных мы имеем дело с двойным пределом, что можно записать в виде

x→a y→b

Можно выбрать конкретный порядок предельного перехода, например,

Пределы, представленные в таком виде, называются повторными. Необходимым и достаточным условием существования двойного предела

(3) является равенство между собой повторных пределов:

При этом двойной предел равен повторным:

19