1.4. Приложения формулы Тейлора

1.5. Примеры применения формулы Тейлора

1.6. Формулы приближенных вычислений

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

Математический анализ

Файл:

Учебник Математический Анализ Конев.pdf

Скачиваний:

202

Добавлен:

16.03.2015

Размер:

2.15 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 323 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Все нижеприведенные формулы вытекают из формулы Маклорена. Единственное, что требуется для их вывода – получить выражения для соответствующих производных n-го порядка.

Для оценки остаточных членов использована форма Лагранжа.

1) Пусть f ( x) = ex . Тогда

f (n) (x) = ex

f (n) (0) =1

для n ≥ 0 , что дает

ex =1 + x +

+... +

+ R ( x)

(12)

Здесь R ( x) =

xn+1 ; c - точка, расположенная между нулем и x .

(n +1)!

Если

x < 0 ,

то

ec <1, так что | R (x)

| <

| x |n+1 .

(n +1)!

2) Пусть f ( x) = sin x . Тогда

kπ

f (k ) ( x) = sin( x +

) ,

f (k ) (0) = sin

Очевидно, что

f (2n−1) (0) = (−1)n−1

(для нечетных k ),

Следовательно,

f (2n) (0) = 0 (для четных k ).

sin x = x −

−... + (−1)n−1

x2n−1

+ R (x)

(13)

(2n −1)!

где |

R (x) | <

| x |2n

для x < 0 ;

| R (x) | <

| x |2n+1

для

x > 0 .

(2n)!

(2n +1)!

3) Пусть f ( x) = cos x . Тогда

Если k – нечетное число, то f

Если же k – четное число, то f Следовательно,

cos x =1 −

−... + (−1)n

x2n

+ R ( x)

(14)

(2n)!

где | R (x) | <

| x |2n+2

для любых x .

(2n + 2)!

4) Пусть f ( x) = arctg x , где −1 < x ≤1. Тогда

arctg x = x −

−... +(−1)n−1

x2n−1

+ R ( x)

(15)

2n −1

Если 0 < x <1, то

| R (x)

| <

| x |2n+1 .

2n +1

5) Пусть f ( x) = ln(1 + x) , где

−1 < x ≤1. Тогда

f (0) =1,

f (n) (x) =

(−1)n−1

(n −1)!,

f (n) (0) = (−1)n−1(n −1)!,

(1 + x)n

что приводит к разложению

ln(1 + x) = x −

−... +(−1)n−1

+ R ( x)

где

R ( x) = (−1)n

xn+1

(1 + c)−n−1 ; | c |<| x | .

n +1

Если 0 < x <1, то

| R (x)

| <

xn+1 .

Пусть f (x) = (1 + x)m , где m - рациональное число. Тогда

f (n) (x) = m(m −1)...(m −n +1)(1 + x)m−n , f (n) (0) = m(m −1)...(m −n


	(1 + x)m =1 + mx + m(m −1) x2 +... + m(m −1)...(m −n +1) xn + R ( x)
		2!	n!	n
		2!	n!
Если m = n ,		то Rn (x) = 0.
Например,		(1 + x)4 =1 +4x +6x2 +4x3 + x4 .

(16)

+1) ,

(17)

Пример 1. Вычислить приближенно 3 e .

Решение: Подставим в формулу (12) x =13 и выберем последовательно n =1,2,3:


1)	ex ≈1 + x					3	e = e1 3 ≈1 +				1	4	≈1.333 ;
											3 =	3
2)	ex ≈1 + x +		x2			3	e ≈1 +	1	+	1	12	=	25	≈1.389 ;
								3					18
	2									2! 3
3)	ex ≈1 + x +	x2		+	x3	3	e ≈1 +	1	+	1	12	+	1	13	=	113 ≈1.395.
								3
	2			6						2! 3			3! 3			81
Любопытно сравнить эти результаты с точным значением:															3	e =1.3956...

Пример 2. Вычислить приближенно sin18°.

Решение. Прежде всего, следует преобразовать градусы в радианы:

18° =

Формула (13) при x =

n =1,2 дает, соответственно:

sin x ≈ x

sin

≈

≈ 0.314 ;

π 3

sin x = x −

sin

≈

− 6

≈ 0.3089 .

Точное значение sin18° равно 0.3090...

Пример 3. Вычислить приближенно 3 10 . Решение. Преобразуем число 10 к виду

10 = 23 +2 = 23 (1 + 223 ) = 23 (1 + 14) .

Тогда	3 10 = 23 1 +	1 .
		4

Теперь можно воспользоваться формулой (17), положив x = 14 и m = 13 .

При n = 2 получаем

3 1 +	1	= 1	+	1	1 3	≈1 +	1	1	+	1 1	(	1	−1)	1	=	155 .
	4			4			3	4		2 3		3		42
																144

Следовательно, 3 10 = 23 1 +1 4 ≈155 72 ≈ 2.1528 .

Точное значение равно 2.1544...

Пример 4. Оценить погрешность вычисления e в зависимости от порядка аппроксимирующего многочлена.

Решение. Рассмотрим остаточный член (12) при x =12 :

R	(	1	) =	ec		1	,
		2		(n +	1)!	2n+1
n

где 0 < c <12 .

Очевидно, что ec < e12 < 2 . Тогда

		R (	1) <			1
		R (	1) <	(n +1)! 2n
		n	2	(n +1)! 2n
R (	1 ) < 0.25,	R ( 1 ) <			1	≈ 0.04 ,	R (	1 ) <		1	≈ 0.005 .
R (	1 ) < 0.25,	R ( 1 ) <		24		≈ 0.04 ,	R (	1 ) <	192		≈ 0.005 .
1	2	2	2	24			3	2	192

f (k ) ( x) = cos(x +

f (k ) (0)

(2n+1) (0) = 0 .

(2n) (0) = (−1)n .

Некоторые полезные приближенные формулы, справедливые для достаточно малых значений x, сведены в таблицу и проиллюстрированы графиками.

Таблица 1

Функция	Первое	Следующее
	приближение	приближение

1 + x

+ 2

sin x

x −

cos x

1 − 2

+ 24

tg x

x + 3

ln(1 + x)

x − 2

1 + x

x +

1 − x

arctg x

x −

1 + x

1 +

−

3 1 + x

1 +

−

1 − x

+ x2

1 + x

+ x2

1 − x

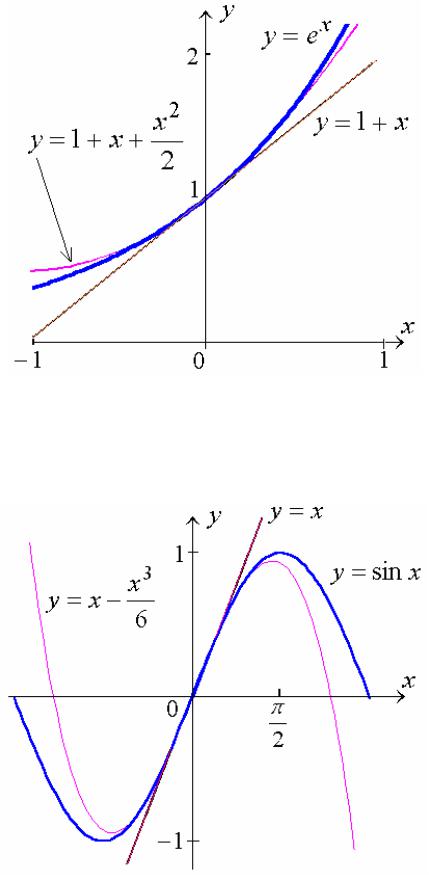
Рис. 1

Рис. 2

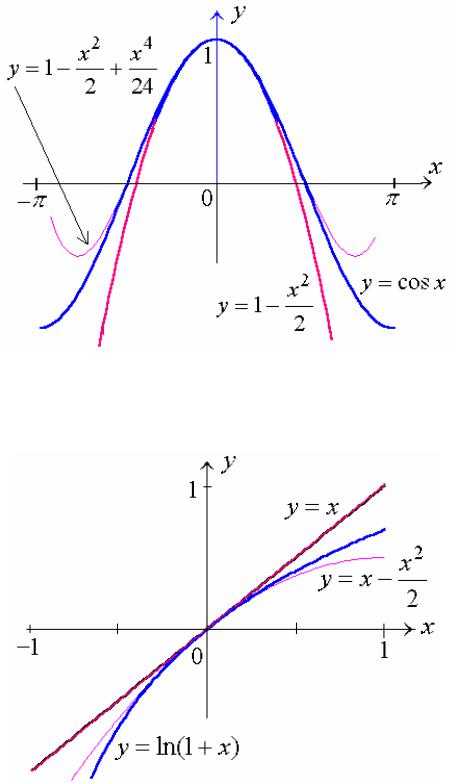
Рис. 3

Рис. 4

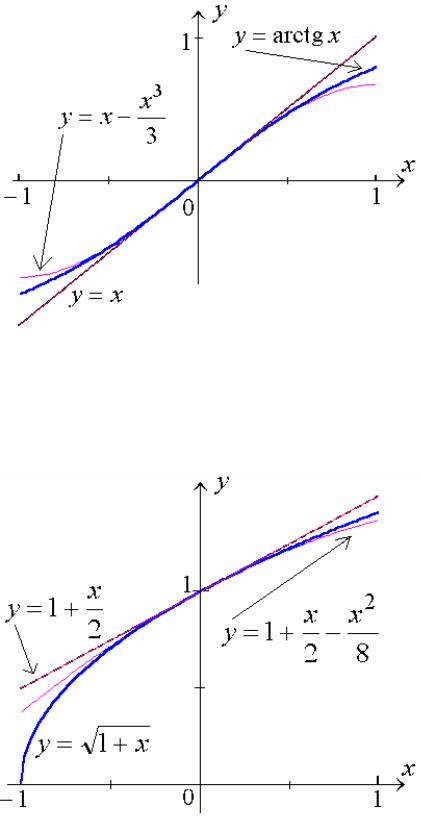
Рис. 5

Рис. 6

<<< < Предыдущая 1 23 / 323 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Математический анализ

#
16.03.2015245.25 Кб49Matan.doc
#
16.03.20151.08 Mб71Matanaliz.pdf
#
16.03.2015295.48 Кб34Матан Лекции.pdf
#
16.03.20152.15 Mб202Учебник Математический Анализ Конев.pdf