
- •ОГЛАВЛЕНИЕ
- •1. ФОРМУЛА ТЕЙЛОРА
- •1.1. Формула Тейлора для многочлена
- •1.2. Формула Тейлора для дифференцируемых функций
- •1.3. Формула Тейлора с остаточным членом в форме Лагранжа
- •1.4. Приложения формулы Тейлора
- •1.5. Примеры применения формулы Тейлора
- •1.6. Формулы приближенных вычислений
- •2. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- •2.1. Основные понятия
- •2.2. Пределы
- •2.3. Непрерывность
- •2.4. Частные производные
- •2.5. Полные дифференциалы
- •2.6. Дифференциалы высших порядков
- •2.7. Дифференцирование сложных функций
- •2.8. Дифференцирование неявных функций
- •2.9. Геометрическая интерпретация частных производных
- •2.11. Экстремумы функций двух переменных
- •3. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
- •3.1. Первообразные
- •3.2. Понятие неопределенного интеграла
- •3.3. Свойства интегралов
- •3.4. Таблица интегралов
- •3.5. Методы интегрирования
- •3.5.1. Метод замены переменной
- •3.5.1.1. Занимательные и поучительные упражнения
- •3.5.1.2. Обобщение таблицы интегралов
- •3.5.1.3. Примеры применения метода
- •3.5.2. Некоторые важные интегралы
- •3.5.3. Интегрирование по частям
- •3.5.3.1. Занимательные упражнения
- •3.5.3.2. Примеры применения метода
- •3.5.3.3. Циклические интегралы
- •Расширенная таблица интегралов
- •3.6. Интегрирование рациональных функций
- •3.6.1. Основные понятия
- •3.6.3. Разложение на простые дроби
- •3.6.3.1. Основная идея метода
- •3.6.3.2. Правила разложения на простые дроби
- •3.6.3.3. Разложение многочлена на множители
- •3.6.3.4. Деление многочлена на многочлен
- •3.6.4. Примеры и упражнения
- •3.7. Интегрирование тригонометрических выражений
- •3.7.5. Универсальная тригонометрическая подстановка
- •3.7.6. Другие тригонометрические подстановки
- •3.8. Интегрирование выражений, содержащих радикалы
- •3.8.2.1. Тригонометрические подстановки
- •3.8.2.2. Гиперболические подстановки
- •3.9. Таблица наиболее важных интегралов
- •3.10. Примеры неберущихся интегралов
- •4. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
- •4.1. Определение
- •4.2. Геометрическая интерпретация
- •4.3. Физическая интерпретация
- •4.4. Свойства интегралов
- •4.5. Основные теоремы
- •Методы интегрирования
- •4.6.1. Интегрирование заменой переменной
- •4.6.2. Интегрирование по частям
- •4.7. Задачи и упражнения
- •4.8. Геометрические приложения определенных интегралов
- •4.8.1. Вычисление площади плоской области
- •4.8.2. Вычисление длины дуги кривой
- •4.8.3. Вычисление объемов тел
- •4.8.4. Задачи и упражнения
- •5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- •5.1. Основные понятия
- •5.2. Признаки сходимости
- •5.3. Примеры исследования интегралов на сходимость
- •5.4. Задачи и упражнения
- •Приложение 1. Гиперболические функции
- •Приложение 2. Полярная система координат
- •Литература
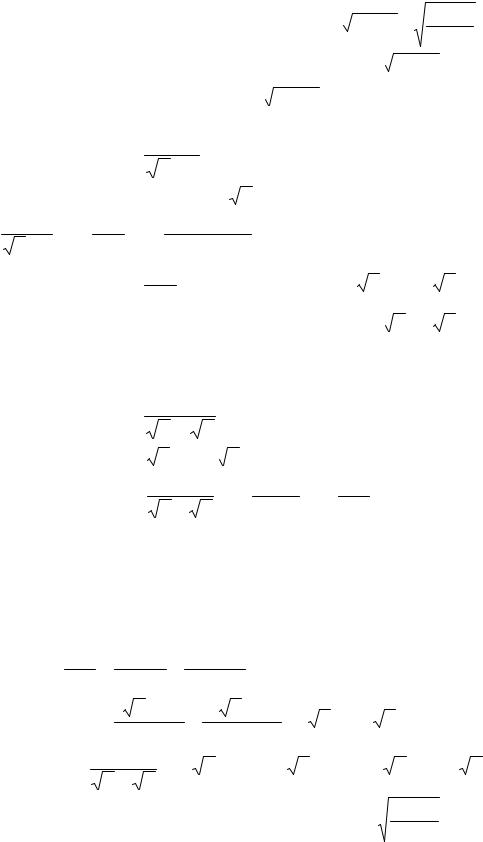
3.8. Интегрирование выражений, содержащих радикалы
|
3.8.1. Иррациональности вида |
n ax +b , n ax +b |
|||||
|
|
|
|
|
|
|
cx +d |
1. Избавление |
от |
иррациональности вида |
n ax +b достигается |
||||
|
|
|
|
|
|
|
1 |
подстановкой ax +b = tn . При этом n ax +b = t и dx = a ntn −1dt . |
|||||||
Пример 1. Вычислить ∫ |
dx . |
|
|
||||
|
|
|
|
x +3 |
|
|
|
Решение. Подстановка x = t2 |
дает x = t и dx = 2tdt . Тогда |
||||||
∫ |
dx |
= 2∫ |
tdt = |
2∫(t +3 −3)dt |
|
|
|
|
x +3 |
|
t +3 |
|
t +3 |
|
|
|
|
= 2∫dt −6∫ |
dt |
= 2t −6ln | t +3 | +C |
= 2 |
x −6ln | x +3 | +C. |
|
|
|
|
|
t +3 |
|
|
|
2.Чтобы одновременно избавиться от радикалов k x и m x , достаточно
сделать подстановку x = tn , где n – наименьшее общее кратное показателей степени k и m.
Пример 2. Вычислить ∫
Подстановка x = t6 дает
∫
Приведем рациональное
t3 |
|
= |
((t |
t + |
1 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x + 3 x . |
|
|
|
|
|
и dx = 6t5dt . Тогда |
|
|||||||||
x = t3 , |
3 x = t2 |
|
||||||||||||||
dx |
|
= 6∫ |
|
t5dt |
2 = 6∫ |
t3dt |
. |
|
|
|
||||||
x + |
3 |
x |
t |
3 |
+t |
t +1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
выражение |
|
t3 |
|
|
к правильной дроби: |
|||||||||||
t |
+1 |
|||||||||||||||
+1) −1)3 |
|
|
|
|
|
1 |
|
|
||||||||
= (t +1)2 −3(t +1) + 3 − |
|
. |
||||||||||||||
t +1 |
|
|
t +1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Интегрируем почленно и затем возвращаемся к исходной переменной x:
∫t3dt |
|
= |
(t +1)3 − 3(t +1)2 |
+3t −ln | t +1| +C |
|
|
||||
t +1 |
|
3 |
|
|
2 |
|
|
|
|
|
|
|
= |
(6 x |
+1)3 |
3(6 x +1)2 |
|
|
|
||
|
|
3 |
− |
2 |
+36 x −ln | 6 x +1| +C. |
|
||||
|
|
|
|
|
|
|
|
|||
Таким образом, ∫ |
|
|
dx3 |
x |
= 2(6 |
x +1)3 −9(6 |
x +1)2 +186 |
x −6ln | 6 |
x +1| +C . |
|
|
|
x + |
|
|
|
|
|
|
||
3. Избавление |
от |
иррациональности |
вида n |
ax +b |
достигается |
|||||
|
|
|
|
= tn . При этом x = tnd −b . |
cx + d |
|
||||
подстановкой |
ax +b |
|
|
|||||||
|
cx +d |
|
|
|
|
a −tnc |
|
|
||
83
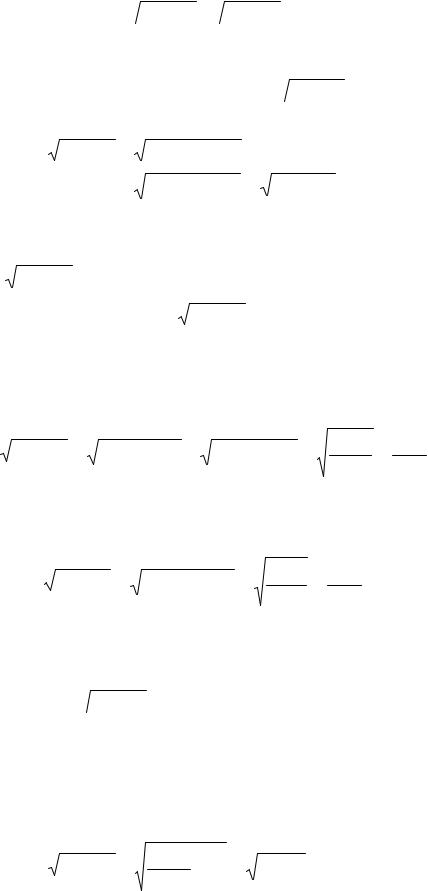
3.8.2. Интегралы, содержащие радикалы вида  a2 ± x2 ,
a2 ± x2 ,  x2 −a2
x2 −a2
3.8.2.1.Тригонометрические подстановки
1.Чтобы избавиться от радикалов вида  a2 − x2 , можно применить тригонометрическую подстановку x = a sin t . При этом
a2 − x2 , можно применить тригонометрическую подстановку x = a sin t . При этом
a2 − x2 = |
a2 −a2 sin2 t |
(59) |
|
= |
a2 (1−sin2 t) = a2 cos2 t = a cost, |
||
|
dx = a costdt .
Тот же эффект достигается с помощью подстановки x = a cosu . В этом
случае a2 − x2 |
= a sin t и dx = −a sin tdt . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2. Иррациональность |
|
|
вида |
|
a2 + x2 |
|
|
устраняется |
|
использованием |
|||||||||||||||||||||
подстановки x = a tg t |
благодаря тригонометрическому тождеству |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 + tg2t = |
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
(60) |
|||||
При этом |
|
|
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
+ x |
2 |
= a |
2 |
+a |
2 |
|
2 |
t = |
a |
2 |
|
|
|
|
2 |
t) = |
|
a2 |
|
= |
a |
, |
(61) |
||||||
|
|
|
|
tg |
|
(1+ tg |
|
cos2 t |
cost |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
adt |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
. |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Другой возможной подстановкой является x = a ctg t , которая влечет |
|||||||||||||||||||||||||||||||
|
|
a |
2 |
+ x |
2 |
|
= |
a |
2 |
|
|
|
2 |
t) = |
a2 |
= |
a |
, |
|
|
|
(62) |
|||||||||
|
|
|
|
|
|
(1 +ctg |
sin2 t |
cost |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
adt |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx = − |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin2 t |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3.Тригонометрическое тождество (60) позволяет также избавиться от радикалов вида  x2 −a2 . Формула (60), записанная в виде
x2 −a2 . Формула (60), записанная в виде
|
|
|
|
|
|
|
1 |
|
−1 = tg2t , |
|
|
|
|
||
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
показывает, что разность x2 −a2 |
представляет собой полный квадрат, |
||||||||||||||
если x = |
a |
. При этом |
dx = |
a sin t |
dt , |
|
|
|
|
||||||
cos t |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|||
|
|
x |
2 |
−a |
2 |
= |
a2 |
|
−a |
2 |
= a |
2 |
2 |
t = a tg t . |
(63) |
|
|
|
|
cos2 t |
|
|
tg |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
84
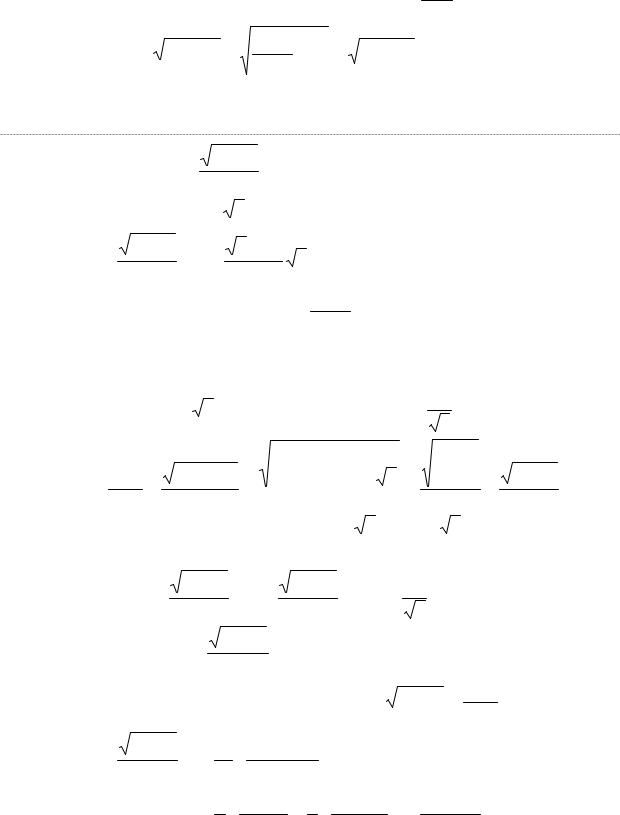
Другой возможной подстановкой являетсяx = sian t , которая дает
|
|
|
x |
2 |
−a |
2 |
= |
|
a2 |
|
−a |
2 |
= |
a |
2 |
2 |
t = a ctg t , |
(64) |
|||||
|
|
|
|
|
sin2 t |
|
|
ctg |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
dx = − a cost dt . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 t |
|
|
|
|
|
|
|||
Пример 1. Вычислить ∫ |
|
3 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
2 |
dx . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Подстановка x = |
|
3 sin t |
дает |
|
|
|
|
|
|
|
|
||||||||||||
∫ |
3 |
− x2 |
dx |
= ∫ |
|
|
3 cost |
|
3 costdt |
|
|
|
|
||||||||||
x |
2 |
3sin |
2 |
t |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
= ∫ctg2tdt = ∫( |
|
t |
−1)dt = −ctg t −t +C. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
||
Решение выражено в терминах переменной t . Чтобы записать его в терминах переменной x , выполним следующие преобразования:
|
|
|
x = |
3 sin t |
|
|
|
|
|
t = arcsin |
x |
, |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
ctg t = cost |
|
|
1−sin2 t |
|
|
|
|
1−sin2 arcsin |
|
|
x |
|
|
|
1− |
|
x2 |
|
3 − x2 . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||||||
= |
|
= |
|
|
|
|
= |
|
|
|
3 |
|
|
= |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
sin t |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||
sin t |
|
|
|
|
|
|
|
sin arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
3 − x2 |
|
|
|
|
|
3 − x2 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x2 |
dx = − |
|
x |
|
−arcsin |
3 |
+C . |
|
|
|
|
|
|
||||||||||||||||||||
Пример 2. Вычислить |
∫ |
9 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
4 |
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||
Решение. Пусть x = 3tg t . Тогда |
dx = |
|
и |
9 + x2 = |
|
|
|
|
|
|
|||||||||||||||||||||||||||
cos2 t |
|
cos t |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫ |
9 + x2 |
|
9 |
∫ |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
4 |
dx = |
81 |
4 |
t cos |
3 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= |
1 ∫costdt4 |
= |
1 |
∫d (sin4 |
|
t) |
= − |
|
1 |
|
|
|
3 |
|
t |
+C. |
|
|||||||||||||||
|
|
|
|
|
|
9 |
|
sin |
t |
|
9 |
sin |
t |
|
|
|
27sin |
|
|
|
|
|
|
||||||||||||||
Осталось записать решение в терминах исходной переменной x . |
|
||||||||||||||||||||||||||||||||||||
Учитывая равенство t = arctg |
x |
|
и тождество tg t = tg(arctg |
x |
) = |
x |
|
, находим |
|||||||||||||||||||||||||||||
|
|
|
3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||
85
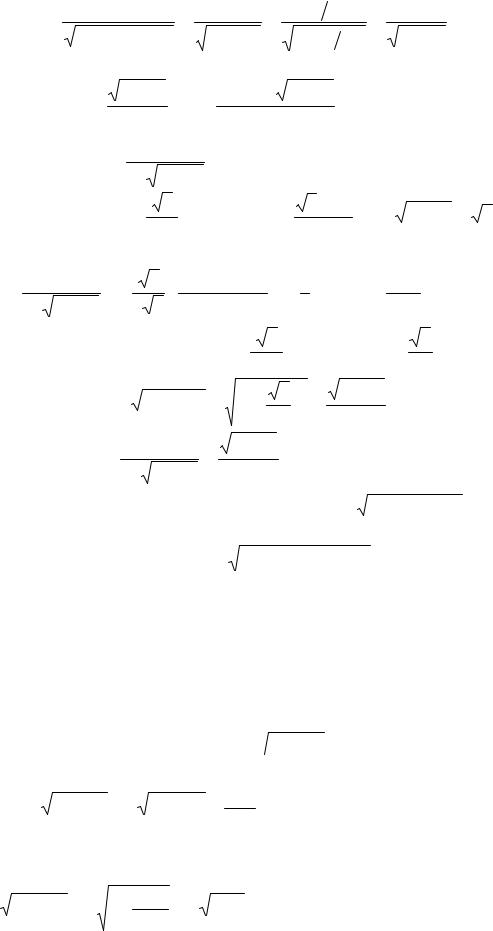
sin t = |
sin t |
|
|
|
= |
|
tg t |
|
|
= |
|
|
x 3 |
= |
|
x . |
|
|||||||||
|
|
cos2 t +sin2 t |
|
|
|
1 + tg2t |
|
1+(x 3)2 |
9 + x2 |
|
|
|||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∫ |
|
9 + x2 |
|
|
|
|
(9 + x2 ) 9 |
+ x2 |
+C . |
|
|
|
|
|
||||||||||
|
|
|
|
x4 |
dx = − |
|
|
|
27x3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 3. |
Вычислить ∫ |
x |
2 |
dx2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
−5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Подстановка x = |
5 |
|
влечет dx = − |
5 cos t dt и |
|
x2 −5 = |
5 ctg t . |
|||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
sin t |
|
|
|
|
|
|
|
|
|
sin2 t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
x2 |
dx |
= − |
5 |
5 ∫cos t sin2 |
2tdt |
= − |
1 |
∫sin tdt = cos t |
+C . |
|
|||||||||||||||
|
x2 −5 |
|
|
|
5 |
|
ctg t sin |
|
t |
|
|
5 |
|
|
5 |
|
|
|
|
|||||||
Выразим cos t |
через переменную x : |
|
x = |
|
5 |
|
|
sin t = |
|
5 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin t |
|
|
|
|
|
x |
|
|
||
|
|
cos u = |
|
|
1 −sin |
2 |
t = |
1 −( |
5 |
) |
2 |
= |
x2 −5 |
. |
|
|
|
|
||||||||
|
|
|
|
|
x |
|
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Окончательно имеем: |
∫ |
x |
2 |
dx2 |
−5 |
= |
|
x2 −5 +C . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
|
|
5x |
|
|
|
|
|
|
|
|
|
|
|||||||
Замечание. |
Чтобы |
избавиться |
|
от |
|
радикалов |
± x2 +bx +c , |
нужно |
||||||||||||||||||
предварительно выделить полный квадрат в выражении под знаком радикала, преобразовав его к виду ±(x −a)2 +const . Затем подстановка y = x −a сводит проблему к одной из вышерассмотренных.
3.8.2.2.Гиперболические подстановки
1. Гиперболическое тождество |
1 − th2 z = |
1 |
|
ch2 z |
|||
|
|
подсказывает сразу две подстановки, x = a th
позволяют устранить радикалы вида a2 − x2 . Действительно, полагая x = a th z , мы имеем
a2 − x2 . Действительно, полагая x = a th z , мы имеем
(см. Приложение 1)
z и x = |
a |
, которые |
|
ch z |
|||
|
|
a2 − x2 = a 1 − th2 z |
= a |
|
, |
dx = |
a |
dz . |
||||
|
ch2 z |
|||||||||
|
|
|
ch z |
|
|
|
||||
Аналогично, подстановка |
x = |
a |
|
дает |
|
|
|
|||
ch z |
dx = − a sh z dz . |
|||||||||
|
1 |
|
|
|
||||||
a2 − x2 = a 1 − |
= a th2 z = a th z , |
|||||||||
|
ch2 z |
|
|
|
|
|
|
|
ch2 z |
|
86

2. Иррациональность вида  a2 + x2 может быть устранена подстановкой
a2 + x2 может быть устранена подстановкой
x = a sh z (благодаря |
тождеству 1+sh2 z = ch2 z ), |
равно как и |
|||
подстановкой x = |
a |
(благодаря тождеству 1 + |
1 |
= cth2 z ). |
|
sh z |
sh2 z |
||||
|
|
|
|||
3. Гиперболическое тождество ch2 z −1 =sh2 z указывает на подстановку x = a ch z , позволяющую избавиться от радикалов вида  x2 −a2 .
x2 −a2 .
Решение. Полагаем
 x2 +a2 = a
x2 +a2 = a
dx .  x2 +a2
x2 +a2
x = a sh z , что влечет dx = a ch z dz . Тогда
sh2 z +1 = a ch z ∫ |
dx |
= ∫dz = z +C . |
|
x2 +a2 |
|
Чтобы выразить z |
через |
x, |
нужно |
предварительно решить |
уравнение |
|||||||
x = a sh z относительно ez |
= t : |
|
|
|
|
|
|
|
|
|
||
x = a (ez −e−z ) |
2x |
= ez |
− |
1 |
|
|
2x |
= t −1 |
|
|||
|
ez |
|
a |
|||||||||
2 |
|
|
|
a |
|
|
|
t |
|
|||
t2 − 2x t −1 = 0 |
t = x |
+ |
|
x2 |
+1 = 1 (x + |
x2 +a2 ) . |
||||||
a |
|
|
|
|
a |
|
|
a2 |
a |
|
|
|
Равенство ez = 1 (x + |
x2 +a2 ) означает, что z = ln( x + |
x2 +a2 ) −ln a . |
||||||||||
a |
|
dx |
|
|
|
|
|
|
|
|
|
|
Таким образом, ∫ |
x |
= z +C = ln(x + |
x2 +a2 ) +const . |
|
||||||||
|
2 +a2 |
|
|
|
|
|
|
|
|
|
|
|
3.8.3. Интегралы вида ∫xm (a +bxn ) p dx
Теорема Чебышева. Пусть m, n и p – рациональные числа. Тогда интеграл
∫xm (a +bxn ) p dx может быть |
представлен в виде конечной |
комбинации |
|||||||||||
элементарных функций, |
если |
и |
только если среди |
чисел |
p , |
m +1 |
и |
||||||
n |
|
||||||||||||
|
m +1 |
|
|
|
|
|
|
|
|
|
|||
|
+ p имеется целое число. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
n |
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Докажем достаточность условий теоремы. |
|
|
|
|
|
||||||||
1) Предположим, |
что число |
p – |
целое. Обозначим через |
s |
наименьшее |
||||||||
|
общее кратное |
знаменателей |
дробей m = m1 m2 |
и n = n1 n2 . Тогда |
|||||||||
|
подстановкой |
x = ts |
интеграл преобразуется |
к |
интегралу |
от |
|||||||
рациональной функции, что решает проблему его вычисления.
87

2) |
Сделаем подстановку xn = z . Тогда |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
1 |
|
|
m+1 |
|
|
||||
|
∫xm (a +bxn ) p dx = ∫z |
|
(a +bz) p |
1 z |
|
−1dz = 1 ∫z |
|
|
−1 (a +bz) p dz . (65) |
|||||||||||
|
n |
n |
n |
|
||||||||||||||||
|
|
m +1 |
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
||||
|
Если |
|
|
– целое число, то подстановка a +bz = tk |
|
(где k – знаменатель |
||||||||||||||
|
|
n |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
дроби рационального числа p) приводит (65) к интегралу от |
|||||||||||||||||||
|
рациональной функции. |
|
|
|
|
|
|
|
|
|
||||||||||
3) |
Выполнив тождественное преобразование, |
представим интеграл (65) в |
||||||||||||||||||
|
виде |
m+1 |
|
|
|
|
m+1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
∫z |
−1 |
(a +bz) p dz = ∫z |
+p−1 ( a +bz ) p dz . |
|
|
|
|||||||||||
|
|
|
n |
|
n |
|
(66) |
|||||||||||||
|
|
|
m +1 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
a +bz |
|
||
|
Если |
|
+ p |
– целое число, |
то подстановкой |
= t s (где k – |
||||||||||||||
|
n |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||||
знаменатель дроби рационального числа p) интеграл (66) преобразуется к интегралу от рациональной функции.
Таблица 5. Подстановки Чебышева.
|
|
|
∫xm (a +bxn ) p dx |
|
|
|
|
|
|
|
|||||
|
Целые |
|
|
|
Подстановки |
|
|
|
|||||||
|
p |
|
|
|
|
|
x = ts , |
|
|
|
|
|
|
|
|
|
где s – наименьшее общее кратное знаменателей |
|
|||||||||||||
|
|
|
рациональных дробей m и n |
|
|
|
|||||||||
|
m +1 |
|
|
|
a +bxn = tk , |
|
|
|
|||||||
|
n |
где k – знаменатель дроби рационального числа p |
|
||||||||||||
|
m +1 + p |
|
|
|
|
a |
|
+b = t |
k |
, |
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|||
|
n |
где k – знаменатель дроби рационального числа p |
|
||||||||||||
|
|
|
|||||||||||||
Пример 1. Вычислить ∫4 1 + x2 dx . |
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Здесь |
p = 1 , |
m +1 |
= |
0 +1 |
= 1 , |
|
|
m +1 |
+ p = |
1 + |
1 = |
3 . |
|||
|
2 |
|
|
||||||||||||
|
|
4 |
n |
2 |
|
|
n |
4 |
2 |
4 |
|||||
Ни одно из этих чисел не является целым.
Следовательно, интеграл не выражается через конечные комбинации элементарных функций.
Пример 2. Вычислить ∫  1+x x2 dx .
1+x x2 dx .
Решение. Запишем интеграл в виде ∫x−1(1+ x2 )1 2 dx .
2 dx .
88
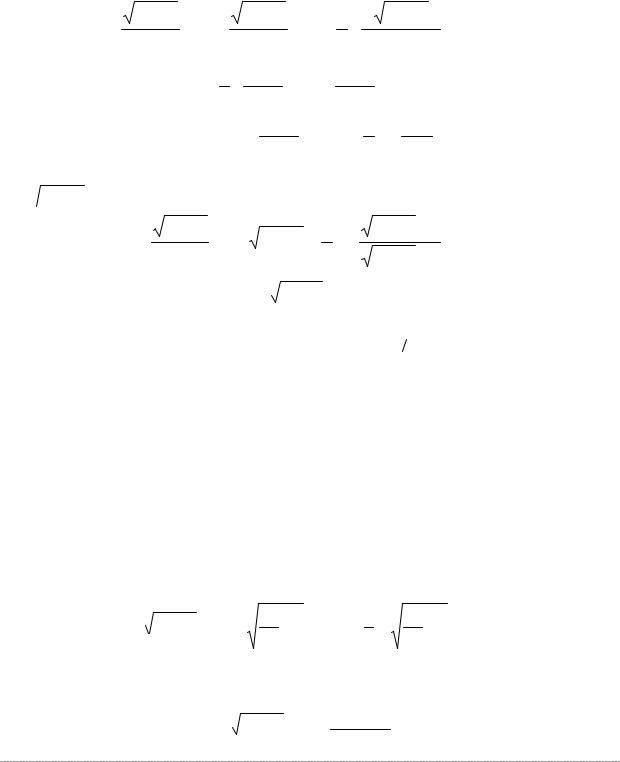
Очевидно, что p = |
1 , m = −1, n = 2 |
|
m +1 |
= |
−1 +1 |
= 0 . |
|||||
n |
|
2 |
|
||||||||
|
|
2 |
|
|
|
|
|
|
|||
Поскольку число |
m +1 |
является целым, то следует применить подстановку |
|||||||||
|
n |
|
|||||||||
x2 +1 = t2 . |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Вычисления будут упрощены, если предварительно преобразовать подынтегральное выражение, выделив комбинацию x2 +1 в явном виде:
∫ |
1 |
+ x2 |
dx = ∫ |
1 |
+ x2 |
xdx = |
1 |
∫ |
|
1 + x2 |
d (x |
2 |
+1) |
|||
|
x |
x |
2 |
2 |
(x |
2 |
+1) |
−1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
=22 ∫t2 t−1 tdt = ∫t2t−2 1 dt
=∫(1 + t2 1−1)dt = t + 12 ln | tt +−11 | +C.
Чтобы вернуться к переменной x, нужно сделать обратную подстановку t =  x2 +1 . Окончательный результат имеет вид
x2 +1 . Окончательный результат имеет вид
|
|
|
∫ |
1 |
+ x2 |
|
2 |
|
1 |
|
|
x2 +1 −1 |
|
|
|
|
|
||||||
|
|
|
|
x |
|
dx = |
x |
|
+1 |
+ 2 ln | |
x2 +1 +1 | +C . |
|
|
|
|
||||||||
Пример 3. |
Преобразовать |
∫x 3 1+ x3 dx |
к |
интегралу |
от |
рациональной |
|||||||||||||||||
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Перепишем интеграл в виде ∫x1(1+ x3 )1 3 dx . |
|
|
|
|
|
||||||||||||||||||
В данном случае p = |
1 |
, m =1, |
n = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверим выполнение условий интегрируемости: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
m +1 |
= 2 , |
|
|
|
m +1 |
+ p = 2 + |
1 =1. |
|
|
|
|
|
|||||||
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
||||||
|
m +1 |
|
|
|
3 |
|
|
|
|
|
|
|
3 |
3 |
1 |
|
|
|
|
||||
Число |
|
+ p является целым, что диктует подстановку |
+1 = t3 . |
||||||||||||||||||||
n |
x3 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
Преобразуем подынтегральное выражение, выделив комбинацию |
|
+1 = t3 |
|||||||||||||||||||||
|
|
||||||||||||||||||||||
в явном виде. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∫x 3 1 + x3 dx = ∫ |
3 13 +1 x2dx = 1 |
∫ 3 13 +1 d (x3 ) . |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
3 |
|
x |
|
|
|
|
|
|
|
Учитывая |
равенства |
|
x3 = (t3 −1)−1 |
и |
|
|
d (x3 ) = −(t3 −1)−2 3tdt , |
приводим |
|||||||||||||||
интеграл к заданному виду: |
|
|
|
|
|
|
3 t2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
∫x 3 1 + x3 dx |
= ∫ |
(t |
|
2 dt . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
−1) |
|
|
|
|
|
|
|
||||
89
