Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Pavlov_V_F_Raschetno-proektirovochnye_raboty.pdf

Скачиваний:

Добавлен:

16.03.2015

Размер:

521.06 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Работа № 3

РАСЧЁТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК

1. ЗАДАНИЕ

Заданы схемы балок, размеры и действующие нагрузки.

Требуется:

построить эпюры Q и M для балок с буквенными данными;

построить эпюры Q и M для балок с числовыми данными, назначить размеры поперечных сечений, сравнить экономичность балок с различными сечениями; провести анализ напряжённого и деформированного состояний в заданной точке одной из балок;

определить прогиб и угол поворота поперечного сечения одной из балок.

В пояснительной записке следует представить реферат, схемы балок, выполненные в масштабе, эпюры Q и M, эпюры σ и τ, элемент балки с действующими на его гранях напряжениями, круг Мора и все необходимые расчёты.

2. ВЫБОР ЗАДАНИЯ

Каждый студент получает от преподавателя шифр, по которому из сборника берёт схемы балок.

Соотношения между нагрузками q, F и m задаются преподавателем. Например,

F = q , m = q22 .

3.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Изображаются в масштабе схемы балок с буквенными данными, вычисляются реакции опор, указываются их значения на схемах. Строятся эпюры поперечных сил Q и изгибающих моментов M с обозначением характерных ординат. Расчёты, сопровождающие решение, в пояснительной записке можно не приводить.

2.Изображаются в масштабе схемы балок с числовыми данными, вычисляются реакции опор, указываются их значения на схемах. Строятся эпюры поперечных сил Q и изгибающих моментов M, подбираются из условия прочности по нормальным напряжениям двутавровые поперечные сечения.

Для одной из балок проводится полная проверка прочности, подбираются, кроме двутаврового, круглое, кольцевое (dD = 0,8), квадратное поперечные

сечения, сравниваются массы балок с различными поперечными сечениями. В расчётах принимается материал балок сталь Ст. 3 с допускаемым на-

пряжением [σ] =160 МПа.

3. Проводится исследование напряжённого и деформированного состояний балки, рассмотренной в п. 2 и имеющей двутавровое поперечное сечение:

•для исследования выбирается сечение с большими значениями поперечной силы и изгибающего момента, строятся эпюры нормальных и касательных напряжений, действующих в этом сечении;

•вычисляются нормальные и касательные напряжения в точке балки, находящейся на расстоянии y = h4 от нейтральной оси, где h – высота сечения;

•в выделенной точке аналитическим и графическим методами определяются главные напряжения, положение главных площадок, наибольшее касательное напряжение и показывается элемент балки в окрестности выделенной точки с изображением всех напряжений на произвольных и главных площадках;

•по найденным значениям главных напряжений вычисляются главные линейные деформации ε1, ε2, ε3, относительное изменение объёма e, удельная энергия деформация u0 и эквивалентные напряжения σэквIII , σэквIV по III и IV

теориям предельных напряженных состояний.

4. Для одной балки с числовыми данными определяются с помощью дифференциального уравнения изогнутой оси балки прогиб и угол поворота сечения, расположенного в середине пролёта двухопорной балки или на свободном конце консольной балки.

П р и м е ч а н и е . По пунктам 2, 3 и 4 в пояснительной записке должны быть представлены все расчёты.

4.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Как определяют поперечную силу и изгибающий момент в произвольном сечении балки?

2.Какие зависимости используют для контроля эпюр поперечных сил и изгибающих моментов?

3.Как распределяются нормальные и касательные напряжения по высоте балки?

4.Какие напряжения называют главными и какими свойствами они обла-

дают?

5.Как вычисляют наибольшие касательные напряжения и на каких площадках они действуют?

6.Как с помощью круга Мора определяют величину и направление главных напряжений?

7.Из каких условий определяют постоянные интегрирования при решении дифференциальных уравнений изогнутой оси балки?

5. ПРИМЕРЫ

Пример 1. Для балки, изображённой на рис. 1, построить эпюры поперечных сил и изгибающих моментов.

Используя уравнения статики, определим реакции опор:

∑M B = 0, q 4 1,5	− RA +q	2 −q 2 16 = 0,	RA =			13		q	;
					16
∑M A = 0, RB −q	2 16 −q 2	+q 4 2 = 0,	RB =			7	q .
				16

Разобьём балку на два участка (рис. 1) и для каждого запишем уравнения Q = Q (z), M = M (z), используя метод сечений.

Участок I: 0 ≤ z1 ≤ 2

Участок II:

0 ≤ z2 ≤

Q = −

+qz2

Q = −

Q (0)= −

q , Q ( )

M = −

q 2

−

qz22

M (0)= 0, M (

= −

q 2

M (0)= −

q 2

, M

( )

= −

q 2

На втором участке эпюра Q плавно пересекает ось, в этом сечении момент достигает экстремальной величины. Для его определения найдём координату этого сечения zэкст из равенства:

Q (zэкст )= 0, т.е. Q (zэкст )= −		7	q	+qzэкст = 0, zэкст =		7	, M (zэкст )=	17	q 2 .
	16				16			512

По вычисленным значениям построим эпюры Q и M (см. рис. 1).

			13		z2			7
F =	q	RA =	16 q	q		RB	=	16 q
F =	4	A				B
	I			II		B
				II
z1				∑q = q
z1		2		∑q = q		m =	q	2
	2						q
	2						16
	9	q
	16			Q
				Q
			+
q	-				-	7
4						7
4						16 q
			17	q 2		16 q
		M	17	q 2
			512
			+
						q 2
		q 2				16
		8
			Рис. 1

Пример 2. Для балки, изображённой на рис. 2, построить эпюры попереч-

ных сил Q, изгибающих моментов M, подобрать размеры кольцевого попе-

речного сечения	α =	d	= 0,75	, если она изготовлена из стали 40. Коэффи-
		D

циент запаса принять равным 1,4.

Используя уравнения статики, определим реакции опор, предварительно задавшись их возможным направлением. Заменим распределённую нагрузку её равнодействующей, которая будет равна площади фигуры этой нагрузки. Приложим её в центре тяжести этой фигуры. В качестве уравнений статики воспользуемся уравнениями моментов относительно шарнирных опор:

∑МВ = 0,	− RA 7	−40 −50 5 + 200 2,5 = 0, RA = 30 кН;
∑МА = 0,	RB 7 −	200 4,5 +50 2 −40 = 0, RB =120 кН.

Для проверки достоверности результатов вычисленных реакций используем уравнение равновесия ∑Y = 0 : 30 +50 −200 +120 = 0.

Реакции определены правильно, укажем их значения на расчётной схеме балки и приступим к построению эпюр Q и М. Для этого разобьём балку на

два участка.
Используя метод сечений, для			каждого	участка составим уравнения
Q = Q (z)	и M = M (z), вычислим их значения на границах участков и по
этим значениям построим соответствующие эпюры.
Участок I: 0 ≤ z1 ≤ 2 м			Участок II: 0 ≤ z2 ≤ 5 м
30 кН	40 кНм M		M				120 кН
		Q	Q


				z2 2 ∑q = 40z2
	z


	1
				z2
	Q = 30 кН			z2
	Q = 30 кН			Q = −120 +40z2
	M = 40 +30z1		M =120z2 −40		z22	=120z2 −20z22
	M = 40 +30z1		M =120z2 −40			=120z2 −20z22
				2
	M (0)= 40 кНм		Q (0)= −120 кН, M (0)= 0
	M (2)=100 кНм		Q (5)= 80 кНм, M (5)=100 кНм

На втором участке эпюра Q меняет знак. В этом сечении момент будет иметь экстремальное значение. Вычислим его величину:

Q (zэкст )= −120 + 40zэкст = 0, zэкст = 3 м,

Мэкст =120 3 −20 32 =180 кНм.

Размеры поперечного сечения определим из условия прочности при изги-

бе по нормальным напряжениям:

наиб

≤[σ].

Допускаемое напряжение определится из соотношения [σ]=

σТ , для ста-

ли 40 σТ = 340 МПа. Момент сопротивления кольцевого сечения определяется

формулой W = πD3		(1−α4 ). С учётом этих значений диаметр балки опреде-
x	32

лится из выражения		D ≥ 3	32	M	наиб nТ	= 3	32 180 103 1, 4	= 0, 223 м.


			σТ π (1−α4 )				340 106 π (1−0,754 )

Округляя, принимаем D = 225 мм, тогда d = 0,75 225 =170 мм.

RА = 30 кН	40 кН/м	RB = 120 кН
	40 кН/м
40 кНм
50 кН	∑q = 200 кН
z1		z2
2 м	5 м
80
30
+
		_
	180	Q, кН
		Q, кН
100		120
40
		M, кНм

Рис. 2

Пример 3. Для балки круглого поперечного сечения, представленной на рис. 3, построить эпюры Q, М и подобрать диаметр, если она изготовлена из стали 20Х.

Определим реакции в опорах, предварительно задавшись их возможным направлением и заменив распределённую нагрузку её равнодействующей. Она будет равна площади треугольника и приложена в его центре тяжести, т.е.

∑q = 1240 8 =160 кН (рис. 3).

∑МА = 0, RB 8 −160 13 8 −40 +40 2 = 0, RB = 48,33 кН,

∑МВ = 0, 40 10 −40 − RA 8 +160 23 8 = 0, RA =151,67 кН.

Проверим достоверность вычисленных реакций:

∑Y = 0, −40 +151,67 −160 +48,33 = 0, −200 +200 = 0.

Реакции найдены правильно.

Для построения эпюр Q и М разобьём балку на 2 участка и для каждого из них запишем уравнения Q = Q (z), M = M (z). Вычислим значения этих уси-

лий на границах участков и по ним построим соответствующие эпюры.

Участок I: 0 ≤ z1 ≤ 2 м

Q = −40 кН

M = −40z1

M (0)= 0, M (2)= −80 кНм

Участок II: 0 ≤ z2 ≤ 8 м

Q = 12 q(z2 ) z2 −48,33

Из подобия треугольников

q(z2 ) = 40 или q (z2 )= 5z2 , тогда z2 8

40 кН

q(z2 )	M		48,33 кН
	M		48,33 кН
	z2 3	∑q =	1	q(z2 ) z2


Q			2
			2

		z2

Q =	1	5z2 z2 −48,33 = 2,5z22	−48,33; M = 48,33z2	−2,5z22	z2	= 48,33z2	−	2,5	z23.
	2				3			3

Q (0)= −48,33 кН, M (0)= 0, Q (8)=111, 67 кН,				M (8)= −40 кНм.

Эпюра Q плавно пересекает ось, поэтому найдём экстремальное значение момента:

Q (zэкст )= 2,5z22экст −48,33 = 0,

zэкст =

48,33

= 4,39 м,

2,5

Мэкст = 48,33 4,39 −

2,5

4,393

=141,66 кНм.

Диаметр балки определим из условия прочности:

d ≥ 3

наиб

nТ

π σТ

По справочным данным находим для стали 20Х σТ = 500 МПа, так как коэффициент запаса не задан, то примем nТ =1,5. Теперь вычислим необходимый диаметр балки:

d≥ 3 32 141,66 103 1,5 = 0,163 м.

π500 106

Округляя, принимаем d =165 мм.

RA = 151,67 кН
40 кН	40 кНм		∑q =160 кН		RВ = 48,33 кН
40 кН/м
	1	8 м	2	8 м
	3		3
2 м			8 м
111,67
Q, кН		+			zэкст
Q, кН		+
-			141,66
40			141,66
40					48,33
М, кНм					48,33
М, кНм
80			Рис. 3
			Рис. 3

Пример 4. Для заданной балки (рис. 4), изготовленной из стали 10, построить эпюры Q, M, подобрать размеры прямоугольного поперечного сече-

ния	h	=1,5	. Руководствуясь эпюрой моментов и условиями закрепления

b

балки, построить ориентировочно её изогнутую ось.

Зададимся возможным направлением реакций, распределённые нагрузки заменим их равнодействующими и определим реакции в опорах.

В балке с промежуточным шарниром D к известным уравнениям статики добавляется ещё одно уравнение – сумма моментов всех сил, расположенных по одну сторону от шарнира, равна нулю. Первым следует использовать уравнение, в котором будет только одна неизвестная реакция. Таким уравнением для данной балки будет сумма моментов всех сил, расположенных справа от шарнира:

∑Мшпр.с = 0, RC 1−80 1 = 0, RC = 80 кН,
∑МA = 0, 80 4 −80			4 + RB 2 −30 1+50 4 3 = 0,				RB = −18,33 кН,
лев.с			1
∑Мш	= 0,	−30 4	+ RA 3 −50	2 +1	+18,33	1	= 0, RA = 61,67 кН.

			3
Проверка:		∑Y = 0, 30 −61,67 +50 −18,33 +80 −80 = 0, 160 −160 = 0.

Реакции определены правильно.

Разобьём балку на 5 участков. Для каждого из них запишем уравнения Q = Q (z) и M (z). Вычислим значения этих усилий на границах участков и построим их эпюры.

Участок I: 0 ≤ z1 ≤1 м

Q = 30 кН, M = 30z1

30 кН

М(0) = 0, M (1) = 30 кНм

Участок II: 0 ≤ z2 ≤ 2 м

61,67 кН

∑q

q(z2 ) z2

Q=30−61,67+

q(z ) z

30 кН

Из подобия треугольников

q(z2 )

q(z2 ) = 25z2 ,

тогда

Q = −31,67 +

25z2 z2 = −31,67 +12,5z22 ,

M = 30 (z2 +1) −61,67 z2 +

12,5z22

= 30 (z2 +1) −61,67 z2 +

12,5

z23.

Q(0) = −31, 67 кН, М(0) = 30 кНм, Q(2) =18,33 кН,

М(2) = 0.

Эпюра Q плавно пересекает ось, в этом сечении следует вычислить экстремальный момент:

Q (zэкст )= −31,67 +12,5zэкст2 = 0, zэкст =

31,67

=1,59 м,

12,5

Мэкст =30 2,59 −61,67 1,59 +

12,5

1,593

= −3,6 кНм.

Участок IV: 1 м ≤ z4 ≤ 2 м

80 кН

1 м

кН

Q = 40 z4 −80

M = 80 (z4 −1)−

40z42

∑

= 20z4

Q (1)= −40 кН, М (1)= −20 кНм

Q (2)= 0, M (2)= 0

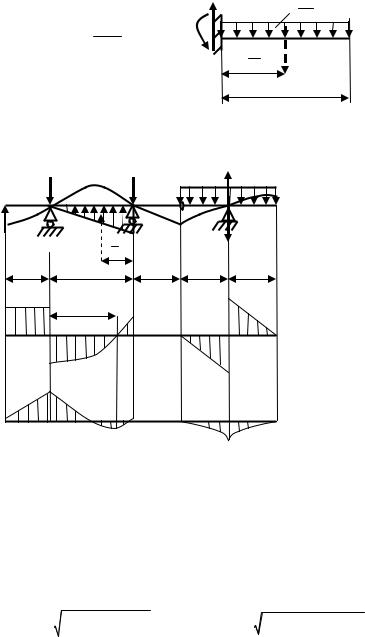
Участок V: 0 ≤ z5 ≤1

кН

40z2

Q = 40z

, M = −

∑q = 40z5

Q (0)= 0, M (0)= 0

Q (1)= 40 кН, М (1)= −20 кНм

На третьем участке Q (z)= 0, M (z)= 0.

По вычисленным значениям Q, M на границах участков построим их

эпюры.

RA = 61,67 кН

RВ = 18,33 кН

RС = 80 кН

III

∑q =50кН

2 м

∑q =80 кН

1 м

2 м

1 м

zэкст

18,33

Q, кН

31,67

М, кНм

3,6

Рис. 4

Пример 5. Для заданного на рис. 5а плоского напряжённого состояния

аналитическим и графическим методами определить величины главных на-

пряжений и положение главных площадок, подсчитать эквивалентное напря-

жение по IV теории предельных напряжённых состояний.

Обозначим

напряжения,

действующие

на

площадках

σα =100 МПа,

τα = 60 МПа, σβ = 20 МПа, τβ = −60 МПа.

Вычислим аналитическим методом величины главных напряжений:

σI,II

(σα +σβ )±

(σα −σβ )

+4τα

(100

+20)±

(100 −20)

+4 60

= 60 ±72,1; σI =132,1 МПа; σII

= −12,1 МПа.

20 МПа			20 МПа
	100 МПа			100 МПа
	100 МПа			100 МПа
				28°
	60 МПа			132 МПа
	60 МПа	12 МПа		132 МПа
		12 МПа
a			б
	Рис. 5

Для графического решения задачи изобразим оси координат σ, τ (рис. 6) и построим в выбранном масштабе точки Dα (σα, τα ) и Dβ (σβ, τβ ), соответст-

вующие напряжениям на заданных площадках. На отрезке DαDβ, как на диа-

метре, строим окружность. Точки пересечения A и В окружности с осью σ дают значения главных напряжений σI и σII.

Покажем точку Dα′ , симметричную точке Dα относительно оси σ. Через крайнюю левую точку круга В и точку Dα′ проведём прямую, которая пока-

зывает направление главного напряжения σI. Измерив соответствующие отрезки и угол, получим:

ОА = σI =132 МПа, ОВ = σII = −12 МПа, ABDα′ = α0 = −28°;

σ1 =132 МПа, σ2 = 0, σ3 = −12 МПа.

Подсчитаем эквивалентное напряжение по IV теории предельных напряжённых состояний:

σэкв.IV = σ12 +σ22 +σ32 −σ1σ2 −σ2σ3 −σ3σ1 = 1322 +(−12)2 +12 132 =138 МПа.

τ, МПа

60						Dα
60
40
40
20								А	σ, МПа
20
B		О
-20	20		40	60	80	100 120 140 160
-20								132
-20
-40
							Dα′	α0

-60
		Dβ							σI

-80
-80

Рис. 6

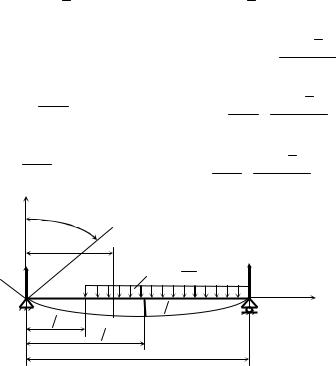
Пример 6. Для балки, изображённой на рис. 7, определить прогиб в середине пролёта и угол поворота сечения, расположенного над левой опорой при следующих данных: материал балки сталь Ст. 3, поперечное сечение двутавр № 30, а, = 8 м, Ix = 7080 см4 .

Выберем начало координат в крайней левой точке балки. Составим дифференциальные уравнения изогнутой оси балки для каждого участка и проинтегрируем их:

Участок I

Участок II

0 ≤ z ≤ 4

4 ≤ z ≤

EIy1′′= RA z

EIy2′′ = RA z −

q z −

RA z2

−

EIy1′

+C1

EIy2′ = RA z

q z

−

+C2

RA z

−

EIy1 =

+C1z + D1

RA z

q z

EIy2

−

+C2 z + D2

RA = 45 кН

q = 20

кН

RB = 75 кН

Рис. 7

Постоянные интегрирования определим из граничных условий:

при z = 0		y1 = 0
при z =	1	y1′ = y2′, y1 = y2
	4
при z =		y2 = 0

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.03.20152.03 Mб57Otvety_proektirovanie_2012.docx
#
07.06.20151.88 Mб10otvety_VED.docx
#
28.03.20165.28 Mб104Ovsepyan В лабиринтах истории отечественной журналистики.pdf
#
16.03.2015209.13 Кб26Past Perfect & Past Perfect Continuous.pdf
#
29.03.20163.01 Mб13Pavlov_V_F_Raschetno-proektirovochnye_raboty.pdf
#
16.03.2015521.06 Кб19Pavlov_V_F_Raschetno-proektirovochnye_raboty.pdf
#
16.03.2015494.76 Кб8PDE.pdf
#
16.03.2015218.4 Кб9Peregruzka_operatsy_Isklyuchenia.pdf
#
07.06.201551.46 Кб6Perevod_na_ekzame_po_anglyskomu.docx
#
07.06.2015383.95 Кб30perevod_stati_po_istorii_tsiklodextrinov-1.rtf
#
16.03.20153.52 Mб32phonetics_book.doc