
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •2. Классическое определение вероятности (ков). Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Формула Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения (зр) дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты, дисперсия и среднеквадратическое отклонение св. Свойства дисперсии.
- •17. Числовые Характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21. Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23. Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24. Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •Понятие о моментах
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения.
- •Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей с.В. И связи между ними.
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства хф.
- •35. Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37. Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38. Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •Способы представления статистических данных
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •Интервальный статистический ряд.
- •Вероятностный смысл гистограммы
- •43. Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44. Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки неизвестных параметров распределения.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример.
- •Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •52. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки гипотезы независимости.
3. Геометрическое определение вероятности. Пример.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Это определение приспособлено для ситуации с континуальным количеством равновероятных исходов, когда классическое определение не работает.
Говорят, что СЭ удовлетворяет геометрическому распределению если:
1.
Исход можно изобразить точками некоторой
области
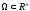 ,
имеющий конечную меру
,
имеющий конечную меру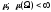 .
.
2.
Можно считать, что попадание точки в
любые области
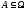 ,
имеющие одинаковую конечную меру
,
имеющие одинаковую конечную меру равновозможное и не зависит от формы и
расположения
равновозможное и не зависит от формы и
расположения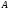 внутри
внутри .
При этом говорят, что точка бросается
наудачу.
.
При этом говорят, что точка бросается
наудачу.
Согласно
геометрическому определению вероятности,
вероятность попадания в любую область
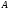 пропорционально ее мере
пропорционально ее мере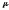 .
.
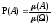 .
.
Рассмотрим
частные случаи: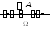
 ;
;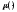 - длина подмножества на числовой прямой
- длина подмножества на числовой прямой .
.
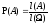

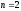 ;
;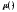 - площадь подмножества на плоскости
- площадь подмножества на плоскости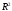 .
.
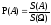
При
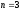 мерой будет являться объем.
мерой будет являться объем.
Из геометрического определения вероятности вытекают свойства:
1.
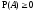 ;
;
2.
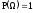 - условие нормировки;
- условие нормировки;
3.
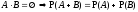 ;
;
Т.к. свойства 1-3 справедливы, то из них вытекают:
4.
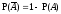 т.к.
т.к.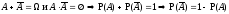 .
.
5.
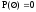 из свойства 4 (
из свойства 4 (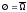 ).
).
6.
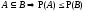 .
.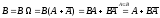 .
Покажем несовместность событий
.
Покажем несовместность событий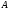 и
и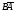 :
: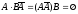 .
Тогда
.
Тогда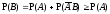 .
.
7.
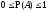 т.к.
т.к.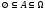 и свойство 6.
и свойство 6.
Пример: Стержень наугад разламывается на 2 части, какова вероятность того, что длины обломков будут отличаться более чем в 2 раза.
Решение:
Исход - точка в которой и сломается стержень.
в которой и сломается стержень.
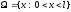 ;
;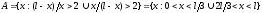 .
.
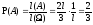 .
.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Сформулировано в 1933 г. Колмогоровым А.Н.
ОпрКласс
подмножеств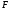 множества
множества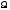 называют
называют -алгеброй,
если выполнены условия:
-алгеброй,
если выполнены условия:
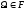 ;
; -
- -алгебра
замкнута относительно перехода к
противоположному событию.
-алгебра
замкнута относительно перехода к
противоположному событию.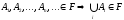 -
- -алгебра
замкнута относительно операции сложения.
-алгебра
замкнута относительно операции сложения.
Утверждения
1-3 называются аксиомами
 -алгебры.
-алгебры.
Покажем,
что
 -алгебра
замкнута относительно произведения и
разности:
-алгебра
замкнута относительно произведения и
разности:

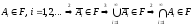 .
.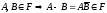 .
.
Множества
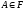 и только они называются случайными
событиями. Пара
и только они называются случайными
событиями. Пара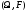 ,
где
,
где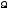 - пространство элементарных событий, а
- пространство элементарных событий, а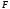
 -алгебра
его подмножеств называетсяизмеримым
пространством.
-алгебра
его подмножеств называетсяизмеримым
пространством.
ОпрПусть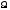 - пространство элементарных событий, а
- пространство элементарных событий, а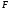
 -алгебра
его подмножеств. Функция
-алгебра
его подмножеств. Функция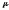 ,
отображающая
,
отображающая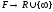 (в вещественную прямую), называется
мерой на измеримом пространстве
(в вещественную прямую), называется
мерой на измеримом пространстве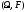 ,
если она удовлетворяет условиям:
,
если она удовлетворяет условиям:
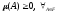 ;
;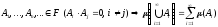 .
.
Последние
2 утверждения называются аксиомами меры
(аксиома неотрицательности и аддитивности).
Мера
 отображающая
отображающая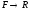 называется нормированной мерой на
измеримом пространстве
называется нормированной мерой на
измеримом пространстве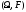 ,
если
,
если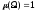 .
.
Пусть
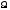 - пространство элементарных событий, а
- пространство элементарных событий, а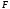
 -алгебра
его подмножеств. Вероятностью или
вероятностной мерой на измеримом
пространстве
-алгебра
его подмножеств. Вероятностью или
вероятностной мерой на измеримом
пространстве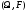 называется функция
называется функция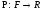 ,
удовлетворяющая следующей системе
аксиом:
,
удовлетворяющая следующей системе
аксиом:
 (аксиома неотрицательности);
(аксиома неотрицательности);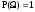 (аксиома нормированности);
(аксиома нормированности);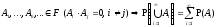 (аксиома счетной аддитивности).
(аксиома счетной аддитивности).
Тройка
 называется вероятностным пространством.
называется вероятностным пространством.
ТеоремаАксиома счетной аддитивности (3) эквивалентна 2-м аксиомам:
3*.
Аксиома конечной аддитивности
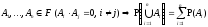 .
.
4.
Если
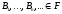 - последовательность событий,
удовлетворяющая:
- последовательность событий,
удовлетворяющая:
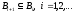 ;
;
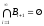 .
.
то
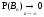 .
Такая последовательность называется
убывающей последовательностью событий.
.
Такая последовательность называется
убывающей последовательностью событий.
Свойства вероятности:
1.
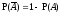 т.к.
т.к.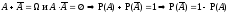 .
.
2.
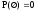 из свойства 1 (
из свойства 1 (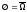 ).
).
3.
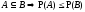 .
.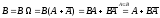 .
Покажем несовместность событий
.
Покажем несовместность событий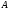 и
и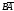 :
: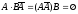 .
Тогда
.
Тогда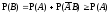 .
.
4.
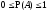 т.к.
т.к.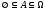 и свойство 3.
и свойство 3.
5.
Теорема сложения вероятностей:
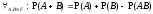 .
.
Доказательство: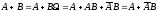 ,
,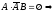 по
аксиоме аддитивности:
по
аксиоме аддитивности:
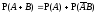 (1).
(1).
Представим
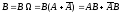 и
и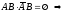 несовместимы
несовместимы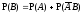 (2).
(2).
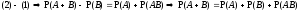 .
.
6.
Если
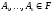 образует ПГС, то
образует ПГС, то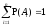 .
Утверждение следует из свойства
вероятности 3* и 4.
.
Утверждение следует из свойства
вероятности 3* и 4.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
