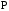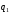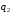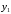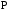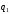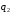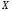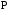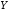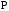- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •2. Классическое определение вероятности (ков). Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Формула Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения (зр) дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты, дисперсия и среднеквадратическое отклонение св. Свойства дисперсии.
- •17. Числовые Характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21. Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23. Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24. Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •Понятие о моментах
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения.
- •Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей с.В. И связи между ними.
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства хф.
- •35. Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37. Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38. Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •Способы представления статистических данных
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •Интервальный статистический ряд.
- •Вероятностный смысл гистограммы
- •43. Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44. Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки неизвестных параметров распределения.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример.
- •Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •52. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки гипотезы независимости.
28. Многомерное нормальное распределение и его свойства.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Рассмотрим
с.в.
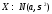 ,
у которой
,
у которой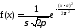 .
.
Опр. Говорят,
что случайный вектор
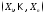 имеет многомерное (
имеет многомерное ( -мерное)
нормальное или Гауссовское нормальное
распределение, если его плотность
вероятности имеет вид:
-мерное)
нормальное или Гауссовское нормальное
распределение, если его плотность
вероятности имеет вид:
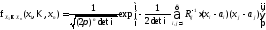 – формула в координатах.,
– формула в координатах.,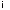 – корреляционная матрица,
– корреляционная матрица,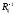 –
алгебраическое дополнение
–
алгебраическое дополнение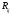 ,
,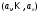 – МО вектора
– МО вектора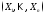 .
.
Из вида
плотности вероятностей следует, что
многомерное нормальное распределение
полностью определяется моментами первых
двух порядков:
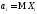 и
и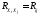 .
.
В матричном виде плотность многомерного нормального распределения записывается так:
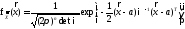 ,
,
где
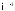 – обратная матрица к
– обратная матрица к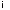 .
В таком виде
.
В таком виде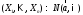 .
.
Пусть
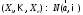 и предположим, что координаты вектора
являются попарно некоррелированными:
и предположим, что координаты вектора
являются попарно некоррелированными: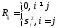 ,
тогда матрица
,
тогда матрица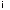 является диагональной:
является диагональной: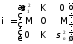 ,
,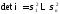 ,
, .
Поэтому из общей формулы в данном случае
имеем:
.
Поэтому из общей формулы в данном случае
имеем:
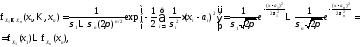
где
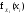 – плотность вероятностей одномерного
нормального закона распределения
– плотность вероятностей одномерного
нормального закона распределения .
Но последнее равенство означает, что
с.в.
.
Но последнее равенство означает, что
с.в. являются независимыми.
являются независимыми.
Таким образом, для нормального ЗР понятие независимости и некоррелированности эквивалентны.
Другие свойства многомерного нормального закона распределения.
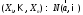 :
:
1.
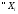 имеют одномерные законы нормального
распределения:
имеют одномерные законы нормального
распределения: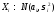 ,
,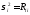
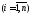 (уметь доказать свойство при
(уметь доказать свойство при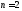 )
)
2) Все условные
ЗР являются нормальными (уметь доказать
свойство при
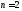 )
)
3) Если
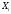 – независимые (некоррелированные), то
– независимые (некоррелированные), то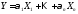 имеет нормальный ЗР:
имеет нормальный ЗР: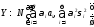 (уметь доказать с помощью интеграла
свертки).
(уметь доказать с помощью интеграла
свертки).
Рассмотрим
подробно двумерный случай. Пусть дан
двумерный вектор ,
а также следующие величины:
,
а также следующие величины: ,
,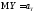 ,
,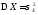 ,
,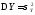 ,
,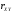 .
Тогда
.
Тогда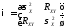 ,
,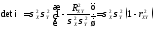 .
.
Легко видеть,
что двумерный нормальный ЗР зависит от
5 параметров:
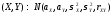 .
Если
.
Если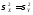 ,
,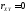 ,
то поверхности уровня – окружности,
тогда НЗР – круговой.
,
то поверхности уровня – окружности,
тогда НЗР – круговой.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
29. Функции от св и их законы распределения.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Функции случайных аргументов
Пусть
![]() - случайный вектор, закон распределения
которого известен, и
- случайный вектор, закон распределения
которого известен, и![]() - скалярная (для простоты) неслучайная
функция, область определения которой
содержит множество возможных значений
вектора
- скалярная (для простоты) неслучайная
функция, область определения которой
содержит множество возможных значений
вектора![]() .
Рассмотрим случайную величину
.
Рассмотрим случайную величину![]() (для того, чтобы функция случайных
аргументов
(для того, чтобы функция случайных
аргументов![]() являлась случайной величиной, функция
являлась случайной величиной, функция![]() должна быть борелевской, см. раздел
«Основная теорема о математическом
ожидании»). Известно, что для нахождения
числовых характеристик случайной
величины
должна быть борелевской, см. раздел
«Основная теорема о математическом
ожидании»). Известно, что для нахождения
числовых характеристик случайной
величины![]() достаточно знать только закон распределения
случайного вектора
достаточно знать только закон распределения
случайного вектора![]() .
Однако, во многих приложениях, особенно
в математической статистике, необходимо
уметь находить в явном виде закон
распределения случайной величиныY,
являющейся функцией случайных аргументов.
Рассмотрим вначале задачу нахождения
закона распределения случайной величины
Y в одномерном
случае (
.
Однако, во многих приложениях, особенно
в математической статистике, необходимо
уметь находить в явном виде закон
распределения случайной величиныY,
являющейся функцией случайных аргументов.
Рассмотрим вначале задачу нахождения
закона распределения случайной величины
Y в одномерном
случае (![]() ).
).
Функции от случайных величин
Дискретный
случай. Пусть![]() – дискретная случайная величина,
принимающая значения
– дискретная случайная величина,
принимающая значения![]() с вероятностями
с вероятностями![]() (случай счетного числа значений случайной
величины
(случай счетного числа значений случайной
величины![]() рассмотреть самостоятельно). Тогда для
произвольной неслучайной функции
рассмотреть самостоятельно). Тогда для
произвольной неслучайной функции![]() ,
область определения которой содержит
множество возможных значений случайной
величины
,
область определения которой содержит
множество возможных значений случайной
величины![]() ,
случайная величина
,
случайная величина![]() является дискретной и задача состоит
в нахождении ее закона распределения.
является дискретной и задача состоит
в нахождении ее закона распределения.
а)
Предположим вначале, что все значения
![]() различны (так, в частности, может быть,
если функция
различны (так, в частности, может быть,
если функция![]() является монотонной в области возможных
значений случайной величины
является монотонной в области возможных
значений случайной величины![]() ).
Тогда случайная величина
).
Тогда случайная величина![]() будет иметь столько же возможных значений
будет иметь столько же возможных значений![]() ,
как и случайная величина
,
как и случайная величина![]() ,
с
,
с![]() и при этом
и при этом
![]() .
(4.1)
.
(4.1)
Таким
образом, закон распределения случайной
величины
![]() имеет вид:
имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
где
в соответствии с (4.1) вероятности
![]() .
.


 б)
Предположим теперь, что среди значений
б)
Предположим теперь, что среди значений![]() есть совпадающие (это может быть, в
частности, если функция
есть совпадающие (это может быть, в
частности, если функция![]() не является монотонной в области
возможных значений случайной величины
не является монотонной в области
возможных значений случайной величины![]() ).
Тогда случайная величина
).
Тогда случайная величина![]() будет иметь меньше возможных значений,
чем случайная величина
будет иметь меньше возможных значений,
чем случайная величина![]() ,
и ими являются
,
и ими являются![]() ,
,![]() ,
различные среди
,
различные среди![]() .
При этом вероятности
.
При этом вероятности![]() значений
значений![]() определяются по формуле:
определяются по формуле: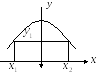
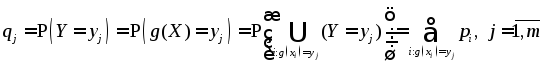 ,
(4.2)
,
(4.2)
Закон
распределения случайной величины
![]() в данном случае имеет вид:
в данном случае имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
где
в соответствии с (4.2) вероятности
![]() являются суммой вероятностей
являются суммой вероятностей![]() тех значений
тех значений![]() ,
для которых
,
для которых![]() .
.![]() ,
,![]() .
.
Пример.
Найти закон распределения случайной
величины![]() ,
если случайная величинаХявляется
дискретной и имеет закон распределения
,
если случайная величинаХявляется
дискретной и имеет закон распределения
|
|
-2 |
-1 |
0 |
1 |
2 |
|
|
0.2 |
0.2 |
0.2 |
0.2 |
0.2 |
Решение.
В соответствии с (4.2) закон распределения
случайной величины![]() имеет вид:
имеет вид:
|
|
0 |
1 |
2 |
|
|
|
0.2 |
0.4 |
0.4 |
|
Непрерывный
случай. Если![]() – непрерывная случайная величина с
плотностью вероятностей
– непрерывная случайная величина с
плотностью вероятностей![]() ,
а
,
а![]() – дифференцируемая функция в области
возможных значений случайной величиныХ, то величина
– дифференцируемая функция в области
возможных значений случайной величиныХ, то величина![]() является непрерывной случайной величиной
и задача состоит в нахождении плотности
вероятностей
является непрерывной случайной величиной
и задача состоит в нахождении плотности
вероятностей![]() .
.
Предположим
вначале, что
![]() -монотонно возрастающаяфункция в
области возможных значений случайной
величиныХ. Тогда у функции
-монотонно возрастающаяфункция в
области возможных значений случайной
величиныХ. Тогда у функции![]() существует однозначная обратная функция
существует однозначная обратная функция![]() и функцию распределения случайной
величины
и функцию распределения случайной
величины![]() можно записать в виде:
можно записать в виде:![]() .
.
Дифференцируя
обе части последнего равенства по
![]() ,
получаем:
,
получаем: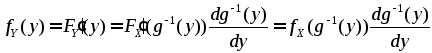 .
(4.3)
.
(4.3)
Для
монотонно убывающейв области
возможных значений случайной величиныХфункции![]()
![]() ,
,
а
после дифференцирования по
![]() обеих частей этого равенства имеем:
обеих частей этого равенства имеем:
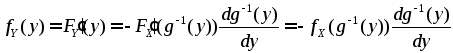 .
(4.4)
.
(4.4)
Объединяя полученные в (4.3) и (4.4) результаты, получаем:
Если
![]() – непрерывная случайная величина с
плотностью вероятностей
– непрерывная случайная величина с
плотностью вероятностей![]() ,
а
,
а![]() – монотонная дифференцируемая функция,
то случайная величина
– монотонная дифференцируемая функция,
то случайная величина![]() является непрерывной и ее плотность
вероятностей
является непрерывной и ее плотность
вероятностей![]() определяется через
определяется через![]() по формуле:
по формуле: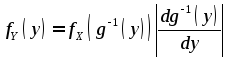 ,
(4.5)
,
(4.5)
где
![]() – функция, обратная к функции
– функция, обратная к функции![]() (отметим, что равенство (4.5) имеет место
только в точках непрерывности плотностей
вероятностей
(отметим, что равенство (4.5) имеет место
только в точках непрерывности плотностей
вероятностей![]() и
и![]() ).
).
Если
дифференцируемая функция
![]() не является монотоннойв области
не является монотоннойв области
возможных
значений случайной величины
![]() ,
то ее область определения можно разбить
на
,
то ее область определения можно разбить
на![]() непересекающихся интервалов, на каждом
из которых она монотонной будет и будет
иметь однозначную обратную функцию
непересекающихся интервалов, на каждом
из которых она монотонной будет и будет
иметь однозначную обратную функцию![]() .
Применяя формулу (4.5) на каждом интервале
монотонности, получаем:
.
Применяя формулу (4.5) на каждом интервале
монотонности, получаем: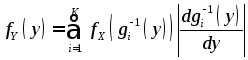 .
(4.6)
.
(4.6)
Пример
1. Пусть![]() – непрерывная случайная величина с
плотностью вероятностей
– непрерывная случайная величина с
плотностью вероятностей![]() ,
а
,
а![]() .
Найти плотность вероятностей
.
Найти плотность вероятностей![]() .
.
Решение.
В данном случае функция![]() является монотонной при любых значениях
является монотонной при любых значениях![]() (при
(при![]() функция
функция![]() возрастает, при
возрастает, при![]() - убывает). Функция, обратная к
- убывает). Функция, обратная к![]() ,
имеет вид:
,
имеет вид:![]() ,
а ее производная
,
а ее производная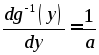 .
Поэтому в соответствии с (4.5):
.
Поэтому в соответствии с (4.5):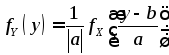 .
(4.7)
.
(4.7)
а)
Рассмотрим линейное преобразование
вида
![]() над случайной величиной
над случайной величиной![]() .
.
В
соответствии с (4.7) в этом случае
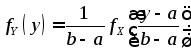 ,
а с учетом того, что
,
а с учетом того, что
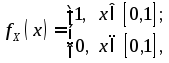
для
плотности вероятностей случайной
величины
![]() имеем выражение:
имеем выражение:
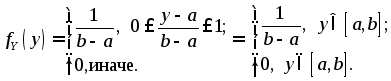
Полученный
результат схематично можно записать в
виде:
![]()
и
он означает, что из равномерного
распределения на отрезке
![]() можно получить равномерное распределение
на любом отрезке
можно получить равномерное распределение
на любом отрезке![]() путем линейного преобразования.
путем линейного преобразования.
б)
Рассмотрим линейное преобразование
вида
![]() над случайной величиной
над случайной величиной![]() .
.
В
соответствии с (4.7) в этом случае
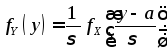 ,
а с учетом того, что
,
а с учетом того, что
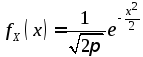
для
плотности вероятностей случайной
величины
![]() имеем выражение:
имеем выражение:
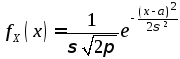 .
.
Полученный результат схематично можно записать в виде:
![]()
и
он означает, что из стандартного
нормального распределения можно получить
нормальное распределение с любыми
параметрами
![]() путем линейного преобразования.
путем линейного преобразования.
Пример
2. Пусть![]() ,
а
,
а![]() .
Найти плотность вероятностей
.
Найти плотность вероятностей![]() .
.
Решение.
В данном случае функция![]() не является монотонной в области
возможных значений случайной величины
не является монотонной в области
возможных значений случайной величины![]() и имеет два интервала монотонности
и имеет два интервала монотонности![]() и
и![]() .
На каждом из интервалов функция
.
На каждом из интервалов функция![]() имеет однозначную обратную функцию:
имеет однозначную обратную функцию:![]() на первом интервале
на первом интервале![]() и
и![]() - на втором
- на втором![]() .
Поскольку модуль производной
.
Поскольку модуль производной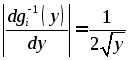 ,
,![]() ,
то в соответствии с (4.6):
,
то в соответствии с (4.6):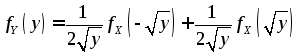 ,
,
а с
учетом того, что
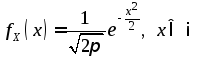 ,
получаем:
,
получаем:
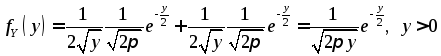 ,
,
![]() при
при![]() .
.
Пример
3. Пусть![]() - строго монотонная функция распределения,
а случайная величина
- строго монотонная функция распределения,
а случайная величина![]() .
Тогда случайная величина
.
Тогда случайная величина![]() имеет заданную функцию распределения
имеет заданную функцию распределения![]() .
.
Решение.
Действительно,![]() .
.
Последнее
равенство следует из того, что функция
распределения случайной величины
![]() имеет вид:
имеет вид:
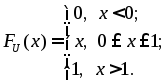 .
.
Смысл
примера 3. Предположим, что требуется
получить![]() значений
значений![]() случайной величины
случайной величины![]() с заданным законом распределения
(смоделировать случайную величину
с заданным законом распределения
(смоделировать случайную величину![]() ).
Для этого в соответствии с примером 3
необходимо найти функцию распределения
).
Для этого в соответствии с примером 3
необходимо найти функцию распределения![]() случайной величины
случайной величины![]() и, если она имеет однозначную обратную
функцию, то положить
и, если она имеет однозначную обратную
функцию, то положить
![]() ,
,![]() ,
,
где
![]() - значения случайной величины, имеющей
равномерное распределение на отрезке
- значения случайной величины, имеющей
равномерное распределение на отрезке![]() (значения
(значения![]() можно получить путем обращения к датчику
случайных чисел, входящему в стандартное
математическое обеспечение любого
персонального компьютера).
можно получить путем обращения к датчику
случайных чисел, входящему в стандартное
математическое обеспечение любого
персонального компьютера).