
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •2. Классическое определение вероятности (ков). Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Формула Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения (зр) дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты, дисперсия и среднеквадратическое отклонение св. Свойства дисперсии.
- •17. Числовые Характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21. Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23. Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24. Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •Понятие о моментах
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения.
- •Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей с.В. И связи между ними.
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства хф.
- •35. Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37. Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38. Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •Способы представления статистических данных
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •Интервальный статистический ряд.
- •Вероятностный смысл гистограммы
- •43. Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44. Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки неизвестных параметров распределения.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример.
- •Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •52. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки гипотезы независимости.
24. Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Рассмотрим
вначале двумерный случайный вектор
 .
.
Прежде,
чем приводить соответствующие определения,
сформулируем обобщение основной теоремы
о математическом ожидании (ОТМО) на
случай функции двух переменных
 .
.
Теорема (обобщение ОТМО на двумерный случай).
Пусть
 - некоторый случайный вектор, закон
распределения которого известен,
- некоторый случайный вектор, закон
распределения которого известен, - неслучайная функция, область определения
которой содержит множество возможных
значений случайного вектора
- неслучайная функция, область определения
которой содержит множество возможных
значений случайного вектора ,
, - случайная величина, являющаяся функцией
двух случайных аргументов.
- случайная величина, являющаяся функцией
двух случайных аргументов.
Если
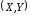 - дискретный случайный вектор, принимающий
значения
- дискретный случайный вектор, принимающий
значения с вероятностями
с вероятностями ,
и ряд
,
и ряд сходится, то у случайной величины
сходится, то у случайной величины существует математическое ожидание и
существует математическое ожидание и .
.Если
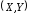 - непрерывный случайный вектор с
плотностью вероятностей
- непрерывный случайный вектор с
плотностью вероятностей и несобственный интеграл
и несобственный интеграл сходится, то у случайной величины
сходится, то у случайной величины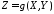 существует математическое ожидание и
существует математическое ожидание и
 .
.
Заметим,
что приведенная теорема очевидным
образом обобщается и на случай функции
 переменных
переменных .
.
Теперь перейдем к рассмотрению числовых характеристик случайных векторов.
Основными
числовыми характеристикамидвумерного
случайного вектора являются:
являются:
математическое ожидание
 - вектор, координатами которого являются
математические ожидания случайных
величин
- вектор, координатами которого являются
математические ожидания случайных
величин и
и (характеризует координаты средней
точки, около которой группируются
другие значения вектора
(характеризует координаты средней
точки, около которой группируются
другие значения вектора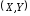 );
);дисперсия
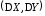 - вектор, координатами которого являются
дисперсии случайных величин
- вектор, координатами которого являются
дисперсии случайных величин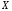 и
и (характеризует степень разброса
(рассеивания) значений вектора
(характеризует степень разброса
(рассеивания) значений вектора около его среднего значения
около его среднего значения );
);корреляционный момент
 случайных величин
случайных величин и
и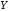 ,
которым называется математическое
ожидание произведения отклонений этих
случайных величин относительно их
математических ожиданий:
,
которым называется математическое
ожидание произведения отклонений этих
случайных величин относительно их
математических ожиданий:
 .
(3.17)
.
(3.17)
Как
будет показано далее, корреляционный
момент
 характеризует степень линейной
зависимости между случайными величинами
характеризует степень линейной
зависимости между случайными величинами и
и .
.
Для
корреляционного момента
 справедливо также следующее выражение:
справедливо также следующее выражение:
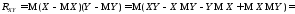
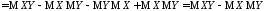 .
.
Таким образом, наряду с (3.12),
 .
(3.18)
.
(3.18)
Корреляционный
момент
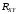 обладает следующими двумя очевидными
свойствами:
обладает следующими двумя очевидными
свойствами:
 ;
; .
.
Благодаря
этим свойствам, вектор дисперсий
 можно не рассматривать как самостоятельную
числовую характеристику, а использовать
объединенную характеристику –
корреляционную матрицу, элементами
которой являются всевозможные
корреляционные моменты:
можно не рассматривать как самостоятельную
числовую характеристику, а использовать
объединенную характеристику –
корреляционную матрицу, элементами
которой являются всевозможные
корреляционные моменты:
 .
.
Таким
образом, можно считать, что случайный
вектор
 имеетдве основные числовые
характеристики:
имеетдве основные числовые
характеристики:
математическое ожидание
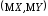 ;
;корреляционную матрицу
 .
.
Математические
ожидания
 и дисперсии
и дисперсии координат случайного вектора
координат случайного вектора могут быть вычислены как по двумерному
закону распределения с помощью обобщения
ОТМО на двумерный случай, так и по обычным
формулам через одномерные законы
распределения случайных величин
могут быть вычислены как по двумерному
закону распределения с помощью обобщения
ОТМО на двумерный случай, так и по обычным
формулам через одномерные законы
распределения случайных величин и
и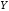 .
.
Так,
если
 - дискретный случайный вектор, то при
- дискретный случайный вектор, то при имеем:
имеем:
 ,
где
,
где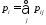 ,
,
а
при
 или
или

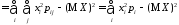 ,
где
,
где .
.
Аналогичны
выражения для
 и
и (написать самостоятельно).
(написать самостоятельно).
Корреляционный
момент
 вычисляется с помощью обобщения ОТМО
на двумерный случай, когда функция
вычисляется с помощью обобщения ОТМО
на двумерный случай, когда функция или
или итолькочерез двумерный закон
распределения:
итолькочерез двумерный закон
распределения:
если
 - дискретный случайный вектор, то
- дискретный случайный вектор, то
 ;
;
если
 - непрерывный случайный вектор, то
- непрерывный случайный вектор, то
 .
.
Многомерный случай.
Основными
числовыми характеристики
 -мерного
случайного вектора
-мерного
случайного вектора являются:
являются:
математическое ожидание
 ;
;корреляционная матрица
 ,
элементами которой являются всевозможные
попарные корреляционные моменты
координат:
,
элементами которой являются всевозможные
попарные корреляционные моменты
координат: .
.
Свойства корреляционной матрицы.
Матрица
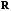 является симметрической размера
является симметрической размера :
: ,
,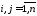 .
.На диагонали матрицы
 расположены дисперсии координат
случайного вектора
расположены дисперсии координат
случайного вектора :
: ,
,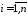 .
.Матрица
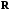 является неотрицательно определенной
матрицей, то есть для любого
является неотрицательно определенной
матрицей, то есть для любого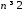 и для любых действительных чисел
и для любых действительных чисел
 .
.
▲
Обозначим
 - центрированную случайную величины,
- центрированную случайную величины, .
Тогда
.
Тогда и для произвольных чисел
и для произвольных чисел имеем:
имеем:

 ■.
■.
Наряду
с корреляционной матрицей
 ,
иногда рассматривают нормированную
корреляционную матрицу
,
иногда рассматривают нормированную
корреляционную матрицу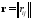 ,
элементами которой являются всевозможные
попарные коэффициенты корреляции
координат:
,
элементами которой являются всевозможные
попарные коэффициенты корреляции
координат: .
Отличие ее от просто корреляционной
матрицы состоит в том, что у нормированной
корреляционной матрицы все диагональные
элементы равны 1:
.
Отличие ее от просто корреляционной
матрицы состоит в том, что у нормированной
корреляционной матрицы все диагональные
элементы равны 1: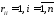 .
.
