
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •2. Классическое определение вероятности (ков). Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Формула Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения (зр) дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты, дисперсия и среднеквадратическое отклонение св. Свойства дисперсии.
- •17. Числовые Характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21. Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23. Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24. Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •Понятие о моментах
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения.
- •Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей с.В. И связи между ними.
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства хф.
- •35. Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37. Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38. Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •Способы представления статистических данных
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •Интервальный статистический ряд.
- •Вероятностный смысл гистограммы
- •43. Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44. Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки неизвестных параметров распределения.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример.
- •Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •52. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки гипотезы независимости.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Эксперимент результат которого может измениться при сохранении условий проведения и непредсказуемым образом называется случайным экспериментом(СЭ).
Всякий факт, который может произойти в результате случайного эксперимента, называется случайным событием (явлением) (СЯ).
Примеры:
СЭ являются: подбрасывание монеты,
игральной кости, 2-х монет, подбрасывание
монеты до выпадения герба, стрельба по
мишени (исход – попадание в точку ,
т.о. множество его исходов не счетное).
,
т.о. множество его исходов не счетное).
1. СЯ, рассматриваемые в ТВ, могут наблюдаться неограниченное число раз, притом в неизменных условиях.
2. СЯ должны обладать свойством статистической устойчивости частот.
ОпрМножество всех возможных взаимоисключающих
исходов СЭ называетсяпространством
элементарных событий. Элементы
множества
всех возможных взаимоисключающих
исходов СЭ называетсяпространством
элементарных событий. Элементы
множества называются элементарными событиями и
обозначаются
называются элементарными событиями и
обозначаются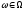 .
.
ОпрПодмножества называютсяслучайными событиями(СС) и обозначаются
называютсяслучайными событиями(СС) и обозначаются .
Говорят, что в результате эксперимента
произошло событие
.
Говорят, что в результате эксперимента
произошло событие ,
если в эксперименте произошел один из
элементарных исходов, входящих в
,
если в эксперименте произошел один из
элементарных исходов, входящих в .
.
Введем операции над СС:
Сумма
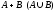 - состоит из всех элементарных исходов
- состоит из всех элементарных исходов или
или .
.Произведение
 - состоит из всех элементарных исходов
и
- состоит из всех элементарных исходов
и и
и .
.
Операции суммы и произведения обобщаются на любое конечное или счетное число событий:
 - сумма;
- сумма;
 - произведение.
- произведение.
Разность

Противоположное событие

 - достоверное событие (происходит всегда
в результате эксперимента). Событие
- достоверное событие (происходит всегда
в результате эксперимента). Событие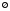 не содержит ни одного элементарного
исхода и называется невозможным.
не содержит ни одного элементарного
исхода и называется невозможным.
Говорят,
что событие
 влечет
влечет (или
(или следует из
следует из )
) ,
если все элементарные исходы
,
если все элементарные исходы событию
событию .
.
События
 (равносильны), если
(равносильны), если и
и .
.
События
 и
и ,
которые не могут произойти одновременно,
т.е.
,
которые не могут произойти одновременно,
т.е. называютсянесовместными.
называютсянесовместными.
Говорят,
что события
 образуют полную группу событий (ПГС),
если они попарно несовместны (т.е.
образуют полную группу событий (ПГС),
если они попарно несовместны (т.е. )
и
)
и .
.
Свойства операций над событиями:
Коммутативность:
 .
.Ассоциативность:
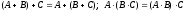 .
.Дистрибутивность:
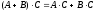 .
. .
.
 .
. .
. .
. - з-ны де Моргана.
- з-ны де Моргана. ,
то
,
то .
.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
2. Классическое определение вероятности (ков). Урновая схема. Пример.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Говорят, что СЭ удовлетворяет КОВ, если:
1.

2. Исходы случайного эксперимента равновозможные.
Исходы можно считать равновозможными, если они обладают свойством симметричности относительно условий проведения экспериментов (т.е. ни один исход не имеет предпочтение перед другим).
Пусть
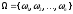 и
и - благоприятствующее событие и
- благоприятствующее событие и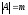 .
Согласно КОВ, за
.
Согласно КОВ, за принимают отношение числа исходов,
благоприятствующих
принимают отношение числа исходов,
благоприятствующих к общему числу исходов:
к общему числу исходов: .
.
Свойства, вытекающие из классического определения вероятности:
1.
 ;
;
2.
 - условие нормировки;
- условие нормировки;
3.
 ;
; .
.
4.
 т.к.
т.к. .
.
5.
 из свойства 4 (
из свойства 4 ( ).
).
6.
 .
. .
Покажем несовместность событий
.
Покажем несовместность событий и
и :
: .
Тогда
.
Тогда .
.
7.
 т.к.
т.к. и свойство 6.
и свойство 6.
Рассмотрим
урновую схему: В урне содержится шаров, из которых
шаров, из которых - белых. Наугад из урны извлекается
- белых. Наугад из урны извлекается шаров. Какова вероятность того, что
среди них окажется ровно
шаров. Какова вероятность того, что
среди них окажется ровно белых?
белых?

 шаров. Общее число исходов
шаров. Общее число исходов .
Число благоприятных исходов:
.
Число благоприятных исходов: .
.

 .
.
Пример: В партии из 100 деталей содержится 5 бракованных. Для контроля наугад отбирают 10 деталей. Какова вероятность того, что среди них окажется хотя бы 1 бракованная.
Решение:
Рассмотрим событие
 ,
тогда
,
тогда
 и
и .
Получим
.
Получим .
.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
