2) Если X – собст. Вектор оператора то вектор , где 0, тоже является собст. Вект. Для собств. Зн. (]

Т. Если – различные собств. значения, то соответствующие им собств. вект.– образуют лин.независ. систему.

(ctv) Пустьне все=0 пусть для определенности . Подействуем преобр.f на обе части(1): (2); ;

(2)-(3) = =0 (*)

Лин. комб. содержит лишь (k-1) векторов. Действуем на (*) преобр. f, затем умножаем (*) на , затем из первого результата вычитаем второй => уничтожится еще один вектор, продолжая данную процедуру, придем к равенству: но тогда = 0, но собственный вектор=> против.

№41

Теорема(Критерий подобия квадратных матриц) Две квадратные матрицы подобны т.и.т.т.к., когда они являются матрицами одного и того же лин. преобр. в разных базисах

Дост. Пусть A и B — квадр. порядка n над полем P, являются матрицами одного и того же лин. преобр. пр-ва V, тогда B=C ^-1AC (*), C-матрица перехода, С

Необ. Существ. Подобные матрицы порядка n–A,B выполняется (*)\

При заданном базисе между квадратичными матрицами n мерного линейного пространства существует взаимно-однозначное соответствие (по цветочку)

Пусть f линейное преобразование пр-ва V, которое в некотором базисе имеет матрицу A, т.к C , то она служит матрицей перехода преобразования f в базисе

№42Алгоритм нахождения собственных значений и собственных векторов линейного оператора

Пусть базис пр-ва V. А f лин. оператор, собственный вектор f=> f(x)=(2)

в (1)=>перепишем (2) как )

ОСЛУ (**) относительно допускает=0 (*). Т.е. нужно решить многочлен n-степени, относительно (характеристич. многочл. преобр. f) => собств. значения обязательно должны быть корнями характерист. уравнения, =>для отыскания необходимо решить(*)

Пусть -корень этого ур. Подставим его в (**) и решим систему относительно , тем самым найдем координаты собственного вектора

Аналогично отыскиваются собственные векторы отвечающие другим собственным значениям

Легко видеть, что множество всех собственных векторов с собственным значением совпадает с множеством всех решений ОСЛУ

№43

Опр. Пусть f лин.опер. n-мерного лин пр-ва V над полем P. Подпространство V’ называется инвариантным относительно f, если для образ . Иначе инвариантно относительно f если.

Теорема. В действительном n-мерном пр-ве V всякий лин.Оператор f имеет по крайней мере одно одномерное или двумерное инвариантное пространство

Пусть - какой-нибудь базис в пр-ве V и пусть - матр. оператора f в этом базисе, тогда многочлен n степени с вещ. коэф. Существует 2 возможных случая: хар. многочлен имеет корень

1)-вещественный. Тогда система для нахождения собст.вектора (*) имеет ненулевое решение, кот.опред. собстве вектор отвеч.

. Очевидно, одномерное подпр. L()-инварант. подпр. относительно f

2)= +i-компл. Подставим корень в сист. (*) получим, что она имеет решение: (‘) Подставляя (‘) в (*), перенесем члены с в правую часть получим

Отделяя вещ и мним. части перейдем к след.сист. (*) и (**)

Введем в рассмотрение векторы и

Ясно, что x,y (собст.векторы). тогда в (*)и (**) примут вид , f(y)=(***),=> подпространство порожденное векторами x и y (L(x,y)) инвариантное подпр. oператора f(x)

Действительно, пусть , f(z)==y=

Размерность. Подпр., т.к. если бы были лин.завис. y=kx, то f(x)= и x был бы собственным вектором преобр с вещ.собств. значением, что невозможно

Следствие: пусть f-лин.оператор вещ. лин. пр-ва Vразмерности (zn+1), где n-натур.,тогда существует хотя бы одно одномерное инвариантное подпр. f, т.к. у f хотя бы один собств.вектор, отвечающий вещ.собст.значению—корню многочлена нечетной степени

№44

Теперь будем считать, что V- евкл.пр-во (т.е. в Vопред. операция скалярного умножения)

Опр. Лин.операторы f и называются сопряженными если имеет место равенство . Очевидно . (1)

Теорема. Пусть f и сопряженные операторы в V, ортонорм. базис вV. А—мат. f, а В — мат в (2). Тогда

Запишем (1) для пары векторов :

( f (),

()

№45

Теорема. В конечномерном евклид. пр-ве V каждый лин. оператор обладает единств.[(!)] сопряженным.

Возьмем в V ортонорм. базис f-лин. преобр. пр-ва, матр f в этом базисе.

Возьмем матрицу (1). Известно, что матрице при заданном базисе отвечает (!) оператор

Покажем, что f и сопряженные операторы.

Из (1)=>(по теореме о матрицах сопряженных операторов) ( f (), (2), т.е. для базисных векторов выполняется соотношение (@)

Возьмем И рассмотрим скаляр. произвед. и

==

=

На основание (2) получаем, что

,

Что означает что соотношение выполняется для , т.е. у лин.оператора f сопряженный—f*. Тогда (@) –

Единственность доказывается (ctv), с помощью утвержд.: «Если u»

№46

Опр. Лин.оператор самосопряженный(сс), если он совпадает со своим сопряжением, т.е. f=f*

Теор. Для того, чтобы оператор был СС необ. и дост., чтобы его матрица в ортонорм. базисе была симметрична

Дост. Пусть А-симм. мат, т.е.. Матрица А соотв.некоторому преобр. f, но тогда соответствует f*. Т.к.f=f*, т.е. f-cc преоб.

Необх. f-cc (f=f*) и его матр.в некотором ортн. базисе, но тогда матрицей f* является (по теореме о матрицах сопряж. операторов). , а это возможно, когда А-симм.

Теорема. Характеристический многочлен с.с.о.f в n-мерн.евкл.пр-ве имеет n действ.корней, среди кот. могут быть одинаковые

(ctv)хар.многчлн имеет компл.корень , при док-ве т.о инвар.прост-вах было установлено, что

, f(y)=(*) и L(x, y)-инв.пр-во с размерностью =z. Из (*)=> левые части равны, вычитая (1)-(2) получим:

0=(т.к.) => =0 –противоречие

№47

Теорема. Если f-сс, то собст.век-ры, отвечающие различным собств.значениям этого преобразования

Пусть различ. собст.зн. СС преобр. f. соотв. собст.век-ры, тогда ;

лев.части равны т.к.f-cc.преоб

№48

Опр. Ортог.дополнением подпр.V_k называется множество всех в-ров из V_n, ортогональных каждому вектору из V_k

Лемма. Ортогональное дополнение k-мерного подпр. V_k есть (n-k)-мерное подпр.

Пусть базис V_k. Вектор т.и.т.т.к. ()=0, …,()=0(*).

Действительно, если (*) выполняется

Обратно, при выполнении (*) xт.к=0

Выберем в V_n ортон.базис и обозначим через -координаты , а через коорд.х. Тогда (*) запишется в виде ОСЛУ в которой k уравнений и n неизвестных

Т.к. её строки являются строками из коэффициентов –лин.незав.(базис)

Совокупность всех решений определяет и, как известно, является(n-k)-мерное подпр.

№49

Теорема. Для всякого сс преобр. найдется хотя бы один ортонорм. базис, состоящий из собст. векторов этого преобр., в кот. матрица преобр. имеет диагональный вид.

Согласно теореме (*)/*Характеристический многочлен с.с.о.f в n-мерн.евкл.пр-ве имеет n действ.корней, среди кот. Могут быть одинаковые*/у с.с.о.f есть дейст.собст.значение x₀, ему отвечает собст.вектор e₁, длину кот.,не нарушая общности можно считать=1.

Пусть Р-совокупность всех векторов P иR имеем , т.е. P P подпр. V являющееся доп. к L(). По лемме[Ортогон. доп. k-мерного подпр. V_k есть (n-k)-мерное подпр.] dimP=n-1. Покажем что P-инвариантное подпр.оператора f

По теореме(*) имеется хотя бы одно вещ.собст.знач. опер-ра f, кот. отвечает соб.вектор P

Продолжая это построение получим n собст.векторов образ.ортон.базис, т.к. f)=обст. зн. f, то матр f в базисе имеет вид

A=

№50

Если - корень кратности m характерист. многочлена самосопряженного преобразования f, то ему соответствуют n-(n-m)=m линейного независимых систем векторов.

Согласно теореме /*для всякого сс преобр. найдется хотя бы один ортонорм. базис, состоящий из собст. векторов этого преобр., в кот. матрица преобр. имеет диагональный вид.*/

базис в кот. матрица преобразования имеет диагональный вид. В этом же базисе

E-A=(*)

Пусть, например корень кратности m характерист.многочлена, т.е. , , тогда в матрице обращаются в 0 m строк, при , а остальные диагональные элементы не равны 0

система = имеет лин.независимых решений собственных векторов, соответствующих собственному значению

1. Опр. лин. пр-ва. След.из аксиом лин. пр-ва. Док.одно

2. Размерность и базис лин. пр-ва. Док., что любой вектор лин. пр-ва можно (!) образом разложить по базису.

3. Док, что если система векторов лин незав. и каждый вектор лин. пр-ва может быть разложен по векторам этой системы, то указанная система векторов является базисом.

4. Необ. и дост. усл. для того, чтобы некоторое подмножество векторов лин пр-ва было лин. подпр. Док, лин обол данной системы векторов лин пр-ва является лин.подпр. этого пр-ва.

5. Док сумма и пересечение двух подпр лин прос являются лин подпр этого пр-ва.

6. Док, что слагаемые подп прямой суммы пересекаются лишь по 0. Док обратное. Необ и дост усл чтобы лин. пр-во являлось прям сум своих подпр. Размерность прямсуммы.

7. Док, что любая квадр невырож мат - матр перех от одного базиса к другому.

8. Т о связи между координ вект в разных базисах.

9. Основная теорема о линейной зависимости.

10. Док, что все макс линейно независимые системы векторов содержат одинаковое количество векторов.

11. Экв системы векторов. Т о == рангов экв систем.

12. Теорема о ранге произведения матриц.

13. Теорема об изоморфизме лин пр-в. Значение теоремы.

14. Док, что мн-во решений ОСЛУ с n, являются лин. подпр пр-ва P^n. Т о размер этого подпр. Т о связи между реш неоднородных и соответствующих однородных систем.

15. Евк пространство. След аксиом скал произв, н-во К-Буняк, н-во , об. т. Пифагора.

16. Док, что любая сист. попарно вект, 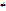0, лин. незав..

17. Т о 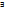ортон базиса. Процесс ортогонализации.

18. Т о представлении скал. произв в координ форме.

19. Теорема об изоморфизме евклидовых пространств.

20. Унит пр-во След аксиом скал произв, н-во К-Буняк, н-во , Ортон базисы, скалярное произведение в координатах.

21. Необ. и дост. усл. симм. (кососим.) билин. формы. Представление билин. формы в виде суммы симм. и косос

22. Преобразование мат билин формы при переходе в лин пр-ве к новому базису. Ранг билинейной формы.

23. Квадре формы. Ранг квадр формы. Т о 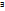базиса, в кот квадр форма имеет канонвид. Метод Лагранжа

24. Метод Якоби приведения квадр формы к канон

25. Кв. формы в вещ лин пр-ве. Закон инерц кв форНеоб признк «+» определ квадр формы. Кр Сильвестра. Следс.

26. Необ и дост условия + полуопределен кв.формы.

27. Необ и дост усл - определ кв формы (след из кр Силь).

28. Теорема о «--» полуопределенности кв формы.

29. Опред Грама. Т об определит Г. Обоб н-ва К-Буняк.

30. Лин преобр (операторы) лин пр-ва. Св-тва

31. Док, что если f и g — лин преоб пр P, то f+g, fg, lg — лин преоб. Полином от линейного преобразования.

32. Матр лин преобр. Т о матрице f+g, fg лин преоб

33. Ранг и ядро лин преобр. Докчто ранг лин преобр == рангу матрицы этого преобразования в любом базисе.

34. Т о связи коорд вект и образа при лин преоб лин пр-ва.

35. Док, невыр преобр -- необ и дост усл его взаим однозн

36. Необ и дост усл обратимос лин опер. (!) обратн опер.

37. Т о завис между матр преобр в разных базисах.

38. Док одно из свойств подобных квадр матриц.

39. Т о == характерист многочленов 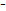мат. Т Гамил-Кэли.

40. Соб зн и собсте век лин преобр. Т о лин незав собст вект., отвечающих различным собственным значениям.

41. Критерий подобия квадратных матриц.

42. Алгоритм нахождения собс век и собст зн лин операт

43. Инвариантные подпр. Теорема об инвар подпр

44. Сопр. операт. Док, что матрицы сопряж опер, в ортонм базисе, то A = B^т.

45. Док, в кон.мер. евк пр-ве кажд лин оп имеет (!) сопр.

46. Необх и досте усл самосопр преоб. Т о корнях характ многочл сс преобр в n-мерном евк пр-ве.

47. Док, в сс преоб собс вект, отвеч разным собст зн пр .

48. Ортог доп подпр. Док, что орт доп k-мерн подпр V^k есть (n-k)-мерное подпр

49. Док, для cc преобр найдется хоть1 ортон базис, сост из собс вект этого преобр, в кот мат пр имеет диагон вид

50. Док, что если l - корень кратн m хар многочл сс преобр f, то ему соответс n-(n-m)=m лин незав систем вект

51. Построение ортон базиса, сост из собст вект сс преоб

52. Орт преоб. Док, что орт преобр переводит ортон базис в ортон базис. Док, лин преоб, переводящее хоть 1 ортон базис в ортон ортогонально.