3.1. Энтропия системы

В теории информации под энтропией системы понимают меру дезорганизованности системы, то есть меру нашего незнания состояния системы.

Понятие энтропии в теории информации, введенное Винером, Шенноном и Колмогоровым [6, 16, 37], базируется (так же, как и в термодинамике) на представлении, что в мире порядок борется с хаосом (дезорганизованностью). Если не прикладывать никаких усилий, то объекты мира становятся более дезорганизованными. Или, по-другому, как состояние хаос более вероятен, чем порядок. Поэтому в естественных условиях состояние системы будет становиться все более дезорганизованным, то есть энтропия системы будет возрастать.

Получение информации, в том числе и о состоянии системы, есть операция по наведению порядка. Эта операция направлена на повышение организованности системы. Следовательно, извлечение информации ведет к снижению энтропии системы, но требует определенных затрат. В такой постановке диагностическая ценность признака определяется тем, насколько уменьшается энтропия системы после определения величины конкретного диагностического признака.

Рассмотрим математическое определение энтропии с позиций теории информации. Первоначально проанализируем факторы, влияющие на энтропию.

1.Допустим, имеется система А, которая может находиться в N случайных состояниях А_i (i = 1....N). Нахождение системы в одном из этих состояний является случайным событием, каждое из которых может появляться с вероятностями P(A₁), P(A₂), ..., P(A_i), ..., P(A_N). Чем больше число состояний, в которых может находиться система, тем больше степень её дезорганизованности. Поскольку степень дезорганизованности определяет энтропию системы, то с увеличением числа состояний энтропия системы будет возрастать. Отсюда следует вывод о том, что математическое выражение для определения величины энтропии должно учитывать количество состояний системы.

2. Будем считать, что события А_i составляют полную группу несовместимых событий, то есть

.

3.Степень дезорганизованности (то есть энтропия системы) зависит не только от числа состояний n, но и от соотношения между вероятностями P(A_i) нахождения системы в каждом из этих состояний. Поясним на примере. Предположим, что система может находиться в трех состояниях A₁, A₂ и A₃. Пусть известны вероятности нахождения системы в этих состояниях Р(А₁); Р(А₂); Р(А₃), причем Р(А₁) = 0,96; Р(А₂) = 0,02; Р(А₃) = 0,02. Очевидно, в такой ситуации заранее можно утверждать, что система вероятнее всего будет находиться в состоянии А₁.

Если Р(А₁) = Р(А₂) = Р(А₃), то дезорганизованность системы будет выше, и следовательно, энтропия больше, чем в первом случае.

Если Р(А₁) = 1, а Р(А₂) = Р(А₃) = 0, то ни о какой дезорганизованности системы говорить не имеет смысла и в этом случае энтропия системы должна быть равна 0.

С учетом этих требований в теории информации энтропия системы А , которая может находиться вN состояниях с вероятностями Р(А_i), определяется следующим соотношением :

, (3.1)

где log₂ - двоичный логарифм.

Рассмотрим основные свойства энтропии, которые в дальнейшем будут использоваться для определения количества информации.

1. Так как вероятность появления события A_i величина положительная и заключена в интервале от нуля до единицы, то есть , то энтропия системы величина также положительная, то есть.

2. Целесообразность использования двоичного логарифма следует из теории связи, поскольку сообщение в одной ячейке памяти может принимать два значения: нуль (событие A₁) или единица (событие A₂) с одинаковой вероятностью, то есть Р(А₁) = Р(А₂) = 0,5. Для такой системы

.

Эта единица измерения называется двоичной единицей или битом. Таким образом, в качестве единицы измерения энтропии принимается степень неопределенности системы, имеющей два возможных равновероятных состояния.

3. Можно ввести понятие энтропии для отдельного состояния А_i:

.

Тогда энтропия системы в целом представляет собой среднее значение энтропии отдельных состояний:

.

Отсюда следует важный вывод, что в случае введения понятия энтропии i-го состояния энтропию всей системы можно вычислять как среднее значение энтропии отдельных состояний:

.

4. Если вероятность одного из состояний Р(А_k) = 1 , то энтропия всей системы H(A) равна 0. Этот вывод вытекает из следующих соображений. Во-первых, в сумме, определенной выражением (4.1), будет слагаемое с индексом k, равное нулю, то есть

.

Все остальные слагаемые при будут иметь неопределенное значение следующего вида:

.

Однако можно доказать, что эта неопределенность в пределе при стремлении к нулю принимает значение, равное нулю:

.

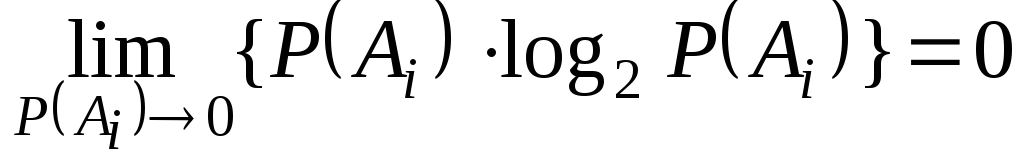Таким образом, в соответствии с выражением (4.1) полная энтропия системы равна нулю: . Это условие очевидно и из физических соображений, так как в подобной системе нет никакой неопределенности.

5.Пусть система может находиться в N равновероятных состояниях, то есть

.

Тогда энтропия системы определится следующим образом:

.

Отсюда следует вывод, что если система может находиться в N равновероятных состояниях, то её энтропия равна логарифму двоичному из числа состояний, то есть H(A) = log₂ N, где N - число состояний.

6.Если система A может находиться в N  состояниях, то энтропия системы максимальна в том случае, когда все состояния равновероятны, то есть

,

при .

Поясним последний вывод на следующем примере. Пусть имеется система А, которая может находиться в двух состояниях (так называемая бинарная система). Известно Р(А₁) , а . Рассмотрим, как будет менятьсяэнтропия системы при различных сочетаниях вероятностей P(A₁) и P(A₂).

В первом варианте примем P(A₁) = 0.

Н(А) Тогда P(A₂) = 1 и, следовательно,

H(A) = 0 (рис. 3.1).

Во втором варианте примем P(A₁) =1.

Тогда P(A₂) = 0 и, следовательно,

0,5 H(A) также равна нулю (рис. 4.1).

В третьем варианте примем, что

вероятности появления первого и

второго состояний одинаковы, то есть

P(A₁)= P(A₂) = 0,5. В этом случае

энтропия системы H(A) максимальна

0 0,5 P(A₁) и равна единице (рис.3.1), то есть

H(A) = max =1.

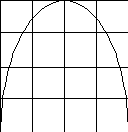
Рис.3.1. Зависимость H(A) бинарной

системы от вероятности первого состояния

Рассмотренные понятия самой энтропии и ее свойства позволяют подойти к вопросу определения количества информации [2, 40].