31. Первый закон термодинамики для изобарного процесса.

В изобарном процессе (P=const). При изобарном расширении газа подведенное к нему количество теплоты расходуется как на увеличение его внутренней энергии и на совершение работы газом:

В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением 

A = p (V2 – V1) = p ΔV.

Первый закон термодинамики для изобарного процесса дает: 

Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV.

При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T₂ < T₁; внутренняя энергия убывает, ΔU < 0.

32. Период колебательного процесса, частота колебательного процесса, единицы измерения.

Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний. (в СИ-с)- Т=1/

Число колебаний в единицу времени называется частотой колебаний(в СИ-Гц)- =1/Т

33. Первый закон термодинамики для изохорного процесса. Внутренняя энергия идеального газа.

первый закон термодинамики, часто записывают так: 

Q = ΔU + A.

В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно, 

Q = ΔU = U (T2) – U (T1).

Здесь U (T₁) и U (T₂) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

При изохорном процессе объем газа остается постоянным, поэтому газ не совершает работу. Изменение внутренней энергии газа происходит благодаря теплообмену с окружающими телами.

Внутренняя энергия — это кинетическая энергия хаотического (теплового) движения частиц системы (молекул, атомов, ядер, электронов) и потенциальная энергия взаимодействия этих частиц.

 

Внутренняя энергия газа, содержащего  частиц, количеством  молей и массой :

Внутренняя энергия зависит от температуры. Если изменяется температура, значит изменяется внутренняя энергия.

34. Функция распределения физической величины. Распределение Максвелла для скоростей молекул газа.

Функция распределения-вероятность того, что величина x находится в промежутке от х₀ до дельта х.

Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного  (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т  скорости, заключенные в интервале от   v  до v + dv.  

Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν), скорости которых находятся в интервале от ν до ν+dν, т. е. 

 откуда  

f (v) - закон распределения молекул идеального газа по скоростям:

 f (v ) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т)

  f(v) зависит от отношения кинетической энергии молекулы, отвечающей рассматриваемой скорости   к величине kT характеризующей среднюю тепловую энергию молекул газа.

Скорости, характеризующие состояние газа:

35. Уравнение изохорного процесса. Его график в координатах PV, PT, VT.

  

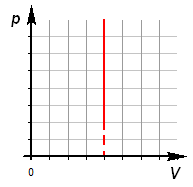
при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или 

Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.

Уравнение изохорного процесса может быть записано в виде: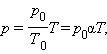 

где p₀ – давление газа при T = T₀ = 273,15 К (т. е. при температуре 0 °С). Коэффициент α, равный (1/273,15) К^–1, называют температурным коэффициентом давления.

36. Амплитудные характеристики вынужденных колебаний. Резонанс. Формула резонансной частоты.

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

37. Уравнение изобарного процесса. Его график в координатах PV, PT, VT.

Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид: 

где V₀ – объем газа при температуре 0 °С. Коэффициент α равен (1/273,15) К^–1. Его называют температурным коэффициентом объемного расширения газов.

Изобарный процесс.

  

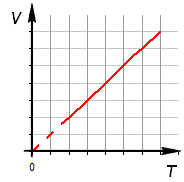
38. Потенциал электростатического поля, единицы измерения. Потенциал поля точечного заряда.

Потенциалом электростатического поля называется физическая величина, равная отношению потенциальной энергии заряда q_пр в данной точке пространства, к величине этого заряда

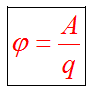
Потенциал поля точечного заряда Q  : _, где e₀-диэлектрическая постоянная 8,85*10^-12 Кл²/Н*м² Потенциал измеряется в Вольтах=Дж/Кл

39. Адиабатический процесс. Уравнение Пуассона.

Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д. 

 первое начало термодинамики в этом случае приобретает вид

где  — изменение внутренней энергии тела,  — работа, совершаемая системой. т. е. внешняя работа совершается за счет изменения внутренней энергии системы.  Используя формулы δA=pdV и C_V=dU_m/dT, для произвольной массы газа перепишем уравнение (1) в виде   (2)  применив дифференцирование уравнение состояния для идеального газа pV=(m/M)RT получим   (3)  Исключим из (2) и (3) температуру Т.    Разделив переменные и учитывая, что С_p/С_V=γ , найдем    Проинтегрируя это уравнение в пределах от p₁ до p₂ и соответственно от V₁ до V₂, и потенцируя, придем к выражению   или    Так как состояния 1 и 2 выбраны произвольно, то можно записать  (4)  Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.  безразмерная величина   (7)  называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, γ=1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i=5, γ=1,4.