
- •Момент инерции (определение, единицы измерения). Моменты инерции цилиндра, шара и стержня относительно оси вращения, проходящей через ось симметрии.
- •Вращательное движение твердого тела с закрепленной осью вращения. Основной закон динамики вращательного движения. Теорема Штейнера.
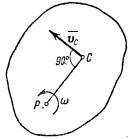
- •Криволинейное движение. Радиус кривизны траектории. Нормальное, тангенциальное, полное ускорение материальной точки.
- •Закон всемирного тяготения (формула Ньютона). Постоянная тяготения (величина, единицы измерения).
- •Связь линейной и циклической частоты. Связь периода гармонических колебаний с циклической частотой.
- •Центр масс системы материальных точек. Закон сохранения импульса системы материальных точек. Принцип реактивного движения.
- •Кинетической энергией системы называется скалярная величина w, равная арифметической сумме кинетических энергий всех точек системы
- •Математический маятник. Частота колебаний математического маятника (формула).
- •Линейная скорость материальной точки, линейное ускорение материальной точки, единицы измерения. Сложение скоростей.
- •Свободные колебания. Пружинный маятник. Частота колебаний пружинного маятника (формула).
- •Первый закон термодинамики для изобарного процесса.
- •Функция распределения физической величины. Распределение Максвелла для скоростей молекул газа.
- •Гармонические колебания. Амплитуда, фаза, циклическая частота гармонических колебаний, единицы измерения.
- •Работа постоянного тока на участке цепи. Закон Джоуля - Ленца.
- •Постоянная Больцмана, её величина, размерность, физический смысл.
- •Правила Кирхгофа. (для электрических цепей, содержащих несколько источников эдс)
- •Среднеквадратичная скорость молекул газа.
- •Колебательная система
- •Напряженность поля точечного заряда
- •Разность потенциалов между двумя точками электростатического поля.
- •Первый закон термодинамики для изотермического и адиабатического процессов.
- •Среднеквадратичная скорость
- •Электрический ток. Сила электрического тока, единицы измерения.
- •Эквипотенциальные поверхности. Эквипотенциальные поверхности для точечного электрического заряда.
- •Поляризация диэлектрика. Напряженность электростатического поля внутри диэлектрика.
- •Реакция деления ядра. Термоядерная реакция (реакция термоядерного синтеза).
- •Закон Ома для участка цепи:
- •Цепная ядерная реакция. Критическая масса радиоактивного элемента
- •Волновая функция (физический смысл).
Кинетической энергией системы называется скалярная величина w, равная арифметической сумме кинетических энергий всех точек системы
![]()
![]() ,
где Vi-скорость
i-й
материальной точки массой mi
,
где Vi-скорость
i-й
материальной точки массой mi
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.
1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки Vi=VC
![]()
или
![]()
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Wне зависит.
2. Вращательное
движение. Если
тело вращается вокруг какой-нибудь
оси Оz (см.
рис.1), то скорость любой его точки ![]() где
где ![]() -
расстояние точки от оси вращения, а
-
расстояние точки от оси вращения, а ![]() -
угловая скорость тела. Подставляя это
значение и вынося общие множители за
скобку, получим:
-
угловая скорость тела. Подставляя это
значение и вынося общие множители за
скобку, получим:
![]()
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
![]()
т.е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение W не зависит.
изменение (приращение) кинетической энергии материальной точки равно работе всех сил, приложенных к этой точке:


-
Потенциальная энергия (определение, единицы измерения). Консервативная система, потенциальные силы.
Потенц.энергия-механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Это энергия взаимодействия тела с Землей. Так как начало отсчета определяется произвольно, то потенц энергия может иметь отрицат.значение.
![]()

Консервативная система –механическая система, при движении которой сумма ее кинетической и потенциальной энергии остается величиной постоянной, т.е. имеет место закон сохранения механической энергии.
![]()
Кинетическая энергия может переходить в потенциальную и обратно в равных количествах Сохранение механической энергии является следствием однородности времени.
Однородность времени означает, что одинаковые физические эксперименты, поставленные в различные моменты времени, дают одинаковые результаты
Потенциальная сила — сила, работа которой при перемещении тела зависит только от начального и конечного положений тела в пространстве. Для непотенциальной силы работа зависит от траектории движения тела между начальным и конечным положениями тела
-
Закон сохранения полной механической энергии системы материальных точек
Механической
энергией или полной механической
энергией называется энергия механического
движения и взаимодействия. Механическая
энергия равна сумме кинетической и
потенциальной энергии.![]()
Если в системе действуют лишь консервативные силы, то полная механическая энергия такой системы остается постоянной. W = const.
![]()
![]() +
+![]()
-
Вынужденные колебания. Каноническое уравнение вынужденных колебаний.
Вынужденные колебания, колебания, возникающие в какой-либо системе под действием переменной внешней силы.

Fo/m - отношение амплитудного значения внешней вынуждающей силы
-
Момент силы (определение, единицы измерения), плечо силы (определение, единицы измерения).
Плечо силы – это перпендикуляр, проведённый из точки опоры на линию действия силы.


Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку А приложения силы, на силы F.

![]()
-
Каноническое уравнение гармонических колебаний.
X’’+w2x=0 , где w- частота гармонических колебаний.
Пример:
движение математического маятника.
![]() -решение
кан.ур.
-решение
кан.ур.
-
Момент импульса вращающегося тела (определение, единицы измерения). Закон сохранения момента импульса.
Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:
|
Поскольку ![]() уравнение
вращательного движения можно представить
в виде:
уравнение
вращательного движения можно представить
в виде:
|
|
Окончательно
будем иметь: ![]() Это
уравнение, полученное здесь для случая,
когда I = const,
справедливо и в общем случае, когда
момент инерции тела изменяется в процессе
движения.
Это
уравнение, полученное здесь для случая,
когда I = const,
справедливо и в общем случае, когда
момент инерции тела изменяется в процессе
движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:
|
ΔL = 0, если M = 0. |
Следовательно,
|
Это и есть закон сохранения момента импульса
