13. Связь линейной и циклической частоты. Связь периода гармонических колебаний с циклической частотой.

Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса. Период колебаний- наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние, в котором он находился в первоначальный момент, выбранный произвольно) Циклическая частота характеризует скорость изменения Фаза колебаний- это величина, которая определяет положение колебательной системы в любой момент времени

Линейная частота - это скалярная физическая величина равная числу колебаний совершаемых системой за единицу времени, измеряется в Герцах

.

14. Центр масс системы материальных точек. Закон сохранения импульса системы материальных точек. Принцип реактивного движения.

Центр масс-воображаемая точка C,положение котрой характеризует распределение массы этой системы. Ее радиус-вектор равен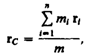

где m_i и r_i — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе;  – масса системы

Закон сохранения импульсов: В замкнутой системе тел векторная сумма импульсов тел не изменяется при взаимодействии тел. Если импульс одного тела увеличился, то это означает, что у какого-то другого тела (или нескольких тел) в этот момент импульс уменьшился ровно на такую же величину.

Закон сохранения импульса — Векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия

  

  

Докажем закон сохранения импульса.

Возьмем и обозначим массы двух тел  и  и скорости до взаимодействия , а после взаимодействия (столкновения) 

По третьему закон Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить 

Для изменений импульсов тел при их взаимодействии на основании . Импульса силы можно записать так

Для первого тела:

  

Для второго тела:

  

И тогда у нас получается, что закон сохранения импульсов выглядит так:

  

Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, или равны нулю, сумма импульсов тел остается неизменной.

Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета

В Формуле мы использовали :

 — Время взаимодействия тел

 — Импульс 1 тела до взаимодействия

 — Импульс 2 тела до взаимодействия

 — Импульс 1 тела после взаимодействия

 — Импульс 2 тела после взаимодействия

Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.Реактивно движение оснвоано на принципе отдачи.

В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью  относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. Тогда для замкнутой системы «ракета + газы» на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия) можно записать: 

где V – скорость ракеты после истечения газов. В данном случае предполагается, что начальная скорость ракеты равнялась нулю.

Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.

15. Длина волны, частота волны, волновое число. Связь между скоростью волны ее длиной и частотой.

ЧАСТОТА ВОЛНЫ, число полных колебаний или циклов волны, совершенных в единицу времени; если за 1 секунду, то измеряется в ГЕРЦАХ

Волновое число -это отношение 2π радиан к длине волны (число волн на длине 2π)

16. Закон равноускоренного движения по прямой, графики зависимости пути и скорости от времени при равноускоренном движении.

равноускоренным движением называют такое движение, при котором вектор ускорения 

 остается неизменным по модулю и направлению. \

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде: 

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y₀ прибавить перемещение за время t: 

Это выражение называют законом равноускоренного движения.

17. Логарифмический декремент затухания, связь с временем релаксации и периодом колебаний.

Логарифмический декремент затухания равен логарифму D:

, N – число колебаний, совершаемых за время уменьшения амплитуды в e раз.

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний умень­шилась в ераз.

Если А(t) и А(t + Т) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение называется декрементом затухания.

18. Кинетическая энергия системы материальных точек (определение, единицы измерения). Связь между приращением кинетической энергии и работой сил, приложенных к телу