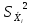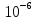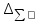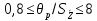metrologia_2_ch_10_zadacha

10. Обработка результатов многократных косвенных измерений.

Определение параметра проводится с помощью прямых многократых измерений параметров 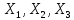, для каждого из которых известны основные метрологические характеристики применяемых средств измерений – пределы измерений (ПИ) и класс точности (КТ).

Исходные данные приведены в таблице 10.1

Таблица 10.1

Измеряемый параметр			Пределы измерений		Класс точности		Вид функции
	15, 42; 15,44; 15,46; 15,46; 15,43	20		0,025
	27,0; 27,4; 26,6; 24,8; 24,5	– 20 …+35		0,2
	5,13; 5,16; 5,15; 5,14; 5,19	0…25		0,04

10.1. Определение оценки истинного значения искомого параметра.

При ограниченном числе измерений () оценкой истинного значения физической величины Z, определяемой как функция случайных величин (аргументов), может служить ее значение , полученное после выполнения вычислительных операций со средними арифметическими значениями аргументов в соответствии с этой функцией, т.е.

.

Среднее арифметическое значение параметров определяем по формуле:

=15,442;

= 27,46

=5,154

Оценка истинного значения параметров с учетом вида ее функции:

.

2. . Определение оценки среднеквадратичного отклонения искомого параметра.

Оценку среднеквадратичного отклонения результата косвенного измерения определяют по формуле:

Где 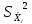- оценка дисперсии результата измерений j – ого аргумента; - частные погрешности косвенного измерения; – коэффициенты корреляции погрешностей всех испытаний j и i, кроме i= j

В тех случаях, когда исходные величины измеряют с помощью

различных средств измерений в разное время, можно полным правом ожидать, что результаты, если и будут коррелированны, то очень мало, и коэффициентом корреляции можно пренебречь, поэтому выражение примет вид

Оценку среднеквадратического отклонения результата измерения j – го аргумента определяем по формуле:

;

;

.

Вычислим частные производные и частные погрешности косвенных измерений по каждому параметру

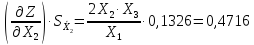
Таким образом, среднее квадратичное отклонение косвенного измерения параметра Z, составляет:

=

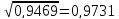
10.3. Определение доверительных границ случайной погрешности.

Доверительную границу случайной погрешности результата косвенного измерения вычисляем по формуле:

Где – коэффициент Стьюдента определяется по таблице для принятого или заданного значения доверительной вероятности и известного эффективного числа степеней свободы

Эффективное число степеней свободы, определяем по формуле

,

Где – число наблюдений, выполненное при измерений j – го аргумента.

Для удобства расчетов составим таблицу

Таблица 10.2

Параметр
	16,2981	265,629	70558,9325	0,0145	0,0002103	0,0442∙
	3,5565	12,6488	159,9923	0,1326	0,01758	0,03091∙
	48,8312	2384,487	5685776,96	0,0103	0,0001059	0,01121∙

При таком числе степеней свободы для доверительной вероятности Р=0,95% интерполяцией данных по таблице находим =2,179. Тогда доверительные границы случайной погрешности

10.4. Определение доверительных границ неисключенной систематической погрешности.

Доверительные граны неисключенной систематической погрешности результата косвенного измерения а случаи, если неискюченной систематической погрешности аргументов заданы границами , вычисляем по формуле

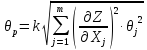
где k – поправочный коэффициент, определяемый принятой доверительной вероятностью Р и m составляющих . Его значения приведены в таблице 10.3

Таблица 10.3 – значение коэффициента k

Р	0,9	0,95	0,98	0,99
k	0,95	1,1	1,3	1,4

В нашем случаи неисключенной систематической аргументов погрешности определяется границами основной погрешности средств измерений.

Так как класс точности всех трех средств измерений указан в виде приведенной погрешности, то в абсолютной форме погрешности средств измерений определяем по формуле:

,

где – нормированное значение, выбираемое в зависимости от шкалы прибора; – приведенная погрешности измерения:

;

;

.

Определяем границы неисключенной систематической погрешности:

, где k=1,1

10.5. Определение доверительных границ суммарной погрешности результата косвенных измерений.

Суммарная погрешность результата косвенных измерений оценивается на основе композиций распределения случайных и неисключенных систематических погрешностей. Формулы для ее расчета в зависимости от соотношения границ неисключенной систематической составляющей и СКО случайной составляющей погрешности приведены в таблице 10.4

Таблица 10.4 – Суммарная погрешность результата косвенных измерений.

Значение	Погрешность результата измерений

определяется по таблице 10.5

Таблица 10.5 – Зависимость от отношения при различной доверительной вероятности.

	0,5	0,75	1	2	3	4	5	6	7	8
	0,81	0,77	0,74	0,71	0,73	0,76	0,78	0,79	0,81	0,81
	0,87	0,85	0,82	0,80	0,81	0,82	0,83	0,83	0,84	0,85

Так как отношение 2,7381, округляем до 3, то для вероятности Р=95% по таблице =0,73,тогда

10.6. Определение доверительных границ систематической погрешности результата косвенного измерения.

Систематическую погрешность, возникающую при косвенных измерениях, при отсутствии корреляции между погрешности аргументов определяем по формуле:

Принимаем .

Результат косвенного измерения при оценках в виде погрешностей измеряемых величин записываем в виде 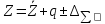при Р=…%

Z=251,67613,4929, при Р=95%