КИС_Лекции / Глава 4

Глава 4 ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЕТЕЙ КОММУТАЦИИ

____________________________________________________________________________________

i =1 j ≠k

Таким образом, в неявном виде получено аналитическое выражение (4.3.9) для расчета функции распределения промежутков времени между вызовами потерянного потока на (х-1) линиях пучка. Любое аналитическое выражение, полученное в неявном виде, обладает, по крайней мере, двумя недостатками.

Во-первых, оно лишено наглядности для анализа зависимости рассчитываемого параметра от исходных данных, поскольку последние в конечном аналитическом выражении отсутствуют.

Во-вторых, дальнейшее использование рассчитанного параметра в качестве составной части другого сложного аналитического выражения еще более усложняет решение и теряет наглядность. Эти причины заставляют искать эмпирическое

Для сравнения (4.3.9) и (4.3.10) в табл. 4.1 приведены результаты расчета функции распределения промежутков времени между вызовами потерянного потока при следующих исходных данных: λ = 10 час -1, μ = 10 час -1 , x = 5. Точное решение вычислялось по формуле

F5 (t) =1−10048.e−0.02t +0.0085e−10.5t −0.0053e−22.5t +0002.e−37.8t −0.0004e−56.8t +0.00003e−82.9t .

Как видно из таблицы в диапазоне t>10*λ-1 приближение вполне пригодно для инженерных расчетов.

В процессе обслуживания вызовов сетью связи каждый узел коммутации каналов анализирует адресную часть поступившего сигнального сообщения и устанавливает соединение в соответствии с таблицей маршрутов. Если возникает дефицит ресурсов (каналов) на пути первого выбора, то на альтернативные пути поступает просеянный поток вызовов, не принятый к обслуживанию на пути первого выбора. На

217

Ю.Ф.Кожанов, Колбанев М.О ИНТЕРФЕЙСЫ И ПРОТОКОЛЫ СЕТЕЙ СЛЕДУЮЩЕГО ПОКОЛЕНИЯ

________________________________________________________________________

последующих узлах происходит объединение собственного потока вызовов с просеянным потоком вызовов.

Рассмотрим фрагмент сети связи, состоящей из трех узлов коммутации (A, B, C), изображенной на рис. 4.13, и проследим прохождение потоков при установлении соединений от узла А к узлу В.

Основной поток вызовов пойдет по пути первого выбора (на рис. 4.13 – жирная линия), при недостаточной емкости основного пучка – по пути второго выбора через узел С (на рис. 4.13 – пунктирная линия). Таким образом, в пучке соединительных линий от узла А к узлу В происходит просеивание потока собственных вызовов узла

разделах было необходимо знать тип и параметры поступающего потока вызовов. Если поток собственных вызовов узла С можно вполне считать простейшим с параметром ΛC , то степень влияния просеянного потока с параметром λA на поток ΛC можно определить, только зная процедуру просеивания потока ΛΑ узлом А. Тогда встают вопросы: как классифицировать суммарный поток вызовов с параметром (ΛC + λA)? В частности, в каких случаях суммарный поток вызовов можно считать простейшим и уверенно пользоваться соответствующими формулами?

ΛC

Рис.4.13. Объединение и просеивание потоков в сети

Ранее были рассмотрены характеристики двух просеянных потоков: в 4.3.3 – потока Эрланга и в 4.3.4 – потока Пальма. На рис. 4.14 для примера показаны: а)порождающий поток вызовов б)просеянный поток Эрланга 4-го порядка и в)потерянный поток Пальма 4-го порядка.

ts

t

а)

t

б)

t

в)

Рис. 4.14. Потоки вызовов а)порождающий поток вызовов б)просеянный поток Эрланга 4-го порядка в)потерянный поток Пальма 4-го порядка

218

Глава 4 ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЕТЕЙ КОММУТАЦИИ

____________________________________________________________________________________

Как видно из рисунка при одинаковой интенсивности просеянных потоков на интервале среднего времени занятия ts характер потоков существенно разнится, хотя они имеют один и тот же параметр потока.

Просеянный поток Эрланга k-го порядка описывается достаточно простым аналитическим выражением

потерянного потока вызовов на полнодоступном пучке приходится производить подмену потока Пальма потоком Эрланга той же интенсивности.

Пусть Λi – параметр простейшего порождающего i-го потока вызовов, λi – параметр просеянного i-го потока вызовов. Тогда процедура классификации суммарного n-мерного потока вызовов сводится к следующему.

1. Определяется эквивалентный параметр порождающего потока вызовов

2. Определяется суммарный параметр просеянного потока вызовов

n

λ s = ∑λ i .

i=1

3.Вычисляется коэффициент просеивания эквивалентного порождающего потока вызовов

k = Λs / λ s – 1.

4. Рекомендуются функции распределения (ФРВО)

ЗАДАЧА 8. Показать, что суммарный поток, полученный объединением простейших потоков, – простейший. Решение.

В этом случае Λi = λ i .

219

Ю.Ф.Кожанов, Колбанев М.О ИНТЕРФЕЙСЫ И ПРОТОКОЛЫ СЕТЕЙ СЛЕДУЮЩЕГО ПОКОЛЕНИЯ

________________________________________________________________________

постепенному снижению значения k = Λ s / λ s – 1 , а это и означает, что по своим свойствам суммарный поток вызовов все более будет приближаться к простейшему.

220

Глава 4 ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЕТЕЙ КОММУТАЦИИ

____________________________________________________________________________________

4.3.5.Модель Энгсета (M/M/V/V/N). Дискретная формула Энгсета

Всистемах распределения информации малой емкости, когда число источников нагрузки (абонентов) мало, параметр потока от одного источника сравним с суммарным потоком вызовов. В этом случае суммарный поток вызовов зависит от числа источников и от состояния {x}, (x=0,1,...V) системы обслуживания. Такой поток

–длительность занятия подчиняется экспоненциальному распределению с параметром μ;

–вызов, не принятый к обслуживанию в момент занятости V линий пучка, теряется, не влияя на моменты поступления последующих вызовов;

–любой из V выходов пучка доступен, когда он свободен, для любого поступающего вызова.

–исходной для расчета является поступающая нагрузка;

–система находится в стационарном режиме.

Подставляя значения параметров λx и μx в формулу (4.3.1) вероятностей

определяет потери по времени и носит название формулы Энгсета.

Рассмотрим источник без потерь. Для него N=V=1, [1] = a – реальная удельная нагрузка, поэтому из (4.3.11)

221

Ю.Ф.Кожанов, Колбанев М.О ИНТЕРФЕЙСЫ И ПРОТОКОЛЫ СЕТЕЙ СЛЕДУЮЩЕГО ПОКОЛЕНИЯ

________________________________________________________________________

Потери по нагрузке

Среднее число занятых линий (обслуженная нагрузка)

Прямой расчет формулы Энгсета во многих практических случаях невозможен из-за переполнения разрядной сетки вычислительного устройства (при больших значениях A и V). Поэтому для ее расчета пользуются рекуррентным соотношением

В инженерной практике при выполнении обеих условий N>>V и N>100 для расчета потерь рекомендуется пользоваться моделью Эрланга, в противном случае следует использовать модель Энгсета.

ЗАДАЧА 14. Определить потери по времени, вызовам и нагрузке для N=5, V=5. Удельная нагрузка a = 0,8 Эрл. Решение.

В нашем случае N=V, поэтому используем модель Энгсета.

ЗАДАЧА 15. Оператор использует для доступа в Интернет учрежденческую АТС на N=50 номеров через пучок V=30 линий. Измерения потерь по вызовам оказались равными 0.026. Оператор хочет снизить потери до значения не более 0.001. Сколько нужно добавить линий ?

Решение.

Из уравнения Pc = E N-1,V (A) при известных значениях Pc =0.026, N=50, V=30 находим параметр свободного источника

A=0.1 Эрланг.

При известных значениях Pc =0.001, N=50, A=0.1 Эрланг находим, что уравнение Pc =0.1 ≥ E N-1,V (A) удовлетворяется при емкости пучка V=35. Следовательно, нужно добавить 5 линий.

4.3.6. Модель Энгсета (M/M/V/V/N). Интегральная формула Энгсета

Пусть {x} – состояние V-линейного пучка (наличие х установленных соединений), [x] – стационарная вероятность состояния {x}, (0 ≤ x ≤ V). Тогда первый потерянный вызов, поступивший на (V+1)-ю фиктивную линию пучка при условии не освобождения занятых линий, будет принадлежать потоку Энгсета (V-x)-го порядка, поскольку потери наступят только после поступления (V-x+1)-го вызова.

222

Глава 4 ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЕТЕЙ КОММУТАЦИИ

____________________________________________________________________________________

Изображение плотности условно потерянного потока Энгсета (V-k)-го порядка имеет вид

Плотность потока условно потерянных вызовов, поступающих на (V+1)-ую a фиктивную линию пучка, находим по формуле полной вероятности

V

fV (t) =[V ](N −V )α e−Nαt ∑CVx (−1)V −x (1+ μ /α )x exαt (μ /α)V −x =

x=0

=[V ](N −V )α e−Nαt ((1+ μ /α)eαt − μ /α)V .

Очевидно,

223

Ю.Ф.Кожанов, Колбанев М.О ИНТЕРФЕЙСЫ И ПРОТОКОЛЫ СЕТЕЙ СЛЕДУЮЩЕГО ПОКОЛЕНИЯ

________________________________________________________________________

где v = V – INT (V) – дробная часть емкости пучка.

Интегральная формула Энгсета используется при расчете потерь в пучке малой емкости при нецелочисленном значении емкости пучка.

4.4.Система с ожиданием (Blocked Calls Queued, BCQ)

4.4.1.Система M/M/V. Стационарные вероятности

Всистеме с ожиданием при недостатке обслуживающих приборов блокированные вызовы становятся в очередь и обслуживаются в порядке поступления. Такая дисциплина обслуживания применяется в маршрутизаторах при использовании алгоритма “с наибольшими усилиями” (Best Effort).

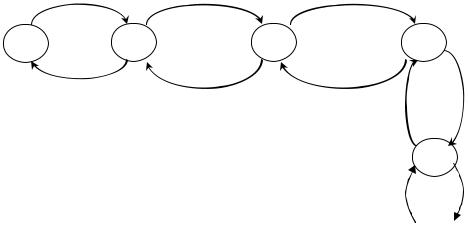
Диаграмма переходов Марковского процесса системы обслуживания с ожиданием изображена на рис. 4.15.

μV λ

V+1

μV λ

. . .

Рис. 4.15. Диаграмма переходов системы с ожиданием

Модель справедлива при предположениях:

–вызовы, поступающие на вход системы, образуют пуассоновский поток постоянной интенсивности с параметром λ;

–длительность занятия подчиняется экспоненциальному распределению с

параметром μ;

– любой из V выходов пучка доступен, когда он свободен, для любого поступающего вызова;

224

Глава 4 ВЕРОЯТНОСТНО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЕТЕЙ КОММУТАЦИИ

____________________________________________________________________________________

–вызов, не принятый к обслуживанию в момент занятости V линий пучка, поступает в очередь и обслуживается в порядке поступления (дисциплина FIFO);

–исходной для расчета является поступающая нагрузка;

–система находится в стационарном режиме.

Используя уравнения стационарного процесса рождения и гибели при A<V, имеем

где [0] определяется из нормирующего условия

Потери по времени равны вероятности того, что все линии заняты, она же – вероятность ожидания начала обслуживания

4.4.2. Система M/M/V. Функция распределения

Обозначим через P(>t) вероятность ожидания начала обслуживания больше, чем t, а через Pk(>t) – условную вероятность ожидания начала обслуживания при поступлении вызова в момент, когда в системе находятся k вызовов, из них V вызовов обслуживаются, а (k-V) вызовов ожидают обслуживания. По формуле полной вероятности

∞

P(> t) = ∑[k]Pk (> t).

k =V

225

Ю.Ф.Кожанов, Колбанев М.О ИНТЕРФЕЙСЫ И ПРОТОКОЛЫ СЕТЕЙ СЛЕДУЮЩЕГО ПОКОЛЕНИЯ

________________________________________________________________________

Вероятность Pk(>t) есть вероятность того, что за время t произойдет не более 1,2,...(k-V) освобождений и вычисляется c использованием распределения Пуассона

При A>V стационарного процесса обслуживания вызовов нет: длина очереди будет монотонно стремиться к бесконечности, каждую единицу времени занятия очередь будет увеличиваться на (A-V) вызовов.

Функция распределения времени ожидания (ФРВО) начала обслуживания Fw(t) или вероятность окончания времени ожидания начала обслуживания за время t

поэтому ФРВО пребывания вызова в системе (ФРВО конца обслуживания вызова)

4.4.3. Система M/M/1

Принимая в формулах (4.4.2) – (4.4.4) значение V=1, A=a, получим:

среднее время ожидания начала обслуживания – tw = λμ μ 1−λ = μa 1−1 a , ФРВО конца обслуживания – F e(t) =1−e−(μ−λ) t =1−e−(1−a) μ t ,

среднее время ожидания конца обслуживания – te = μ 1− λ ,

вероятность нахождения вызова (пакета) на k-ом месте ожидания – [k] = ak +1 (1− a) ,