Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TT_v2.0.pdf

Скачиваний:

Добавлен:

15.03.2015

Размер:

1.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

3.5 Рекуррентная формула Эрланга

A Ai−1

Ei , i ( A) =

(i−1)!

= ...

∑

+...+

Ai−1

+...+

Ai−1

(

(0!

j=0 j!

(i−1)!)

(i−1)!

... =

= ...

(

Ai−1

)

i+A Ei−1, i−1( A)

+...+

Ei−1, i−1( A)

Ei−1, i−1 ( A) i

(i−1)!

Ai−1

(i−1)!

... =

A Ei−1, i−1 ( A)

i+A Ei−1, i−1 ( A)

Ei , i ( A)=

A Ei−1, i−1 ( A)

i=0,1,… ,v

i+A Ei−1, i−1 ( A)

E0, 0 ( A)=1 , i=0

E1, 1( A)=1A+1A , i=1

Остальные значения — в таблицах Пальма.

Перейти к оглавлению>>>

strelnikov.ws

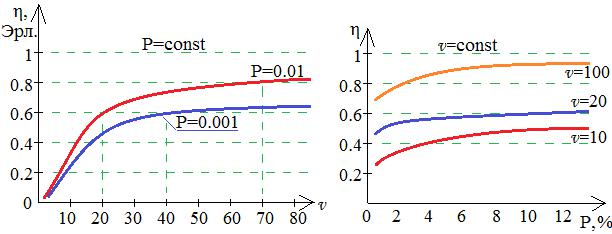
3.6Средняя пропускная способность линий полнодоступного пучка

Средняя интенсивность нагрузки, обслуживаемой одной линией полнодоступного пучка v :

η=

Y обсл

, Y обсл=Y −Y пот=Y −Ev(Y ) Y =Y [1−Ev , v(Y )]

Pv и Pv−1

Записывая выражение для

, легко убедиться, что:

Pv=Y Pv−1 или

Ev , v

(Y )=Y Ev−1, v (Y )

Y обсл , получим:

Подставляя отсюда

Y в выражение для

Y обсл=v

Ev , v (Y )

[1−Ev , v (Y )]

Ev−1, v (Y )

η=

Ev , v

(Y )

[1−Ev , v(Y )]

Ev−1, v (Y )

При малой величине потерь:

η≈

Ev , v (Y )

η= f (v) при

P=const .

Ev−1, v(Y )

Отсюда вывод: для повышения использования линий в пучках необходимо укрупнять пучки. Эффект от объединения пучков тем выше, чем меньше их ёмкость. При v>100 приращение пропускной способности незначительно (кривая почти параллельна оси).

Перейти к оглавлению>>>

strelnikov.ws

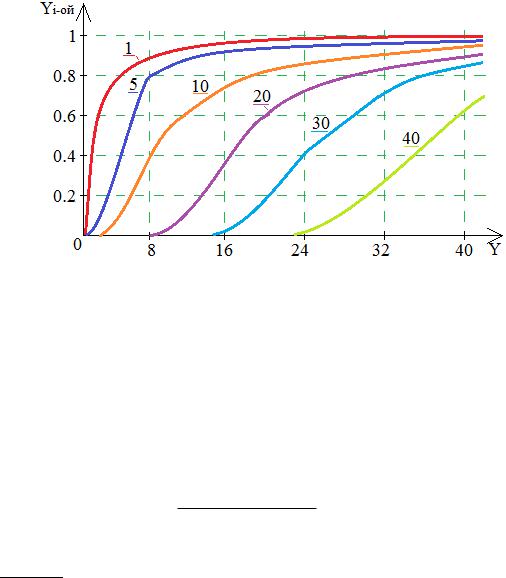
Нагрузка, обслуживаемая i -ой линией пучка при упорядоченном искании, может быть определена из выражения:

Y i−ой=Y 0 i−Y 0 i−1=A [1−Ei , i (A)]−A [1−Ei−1, i−1( A)]=A [ Ei−1, i−1( A)−Ei , i (A)]

Где Y i−ой — интенсивность обслуженной нагрузки пучком из i линий.

Замечание 1. При

v →∞ формула Эрланга может быть заменена

формулой Пуассона:

Y v

Y i

−Y

Ev (Y )=

→

, так как

lim ∑

∑

v →∞ i=0

i=0

Замечание 2. Формула Эрланга Ei , v(Y ) позволяет вычислить вероятность занятия i любых (случайных) линий в пучке из v линий. Часто требуется определить вероятность занятия определённых (фиксированных) линий i из общего числа v (остальные линии могут находиться в любой ситуации). Эта вероятность, как доказал Кони Пальм, определяется из выражения:

Hi= EEv(YY)

v−i ( )

Перейти к оглавлению>>>

strelnikov.ws

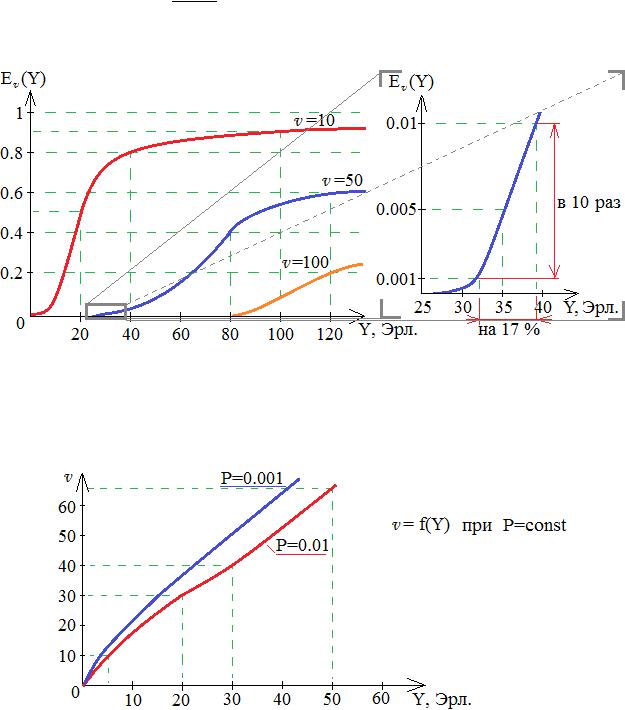
3.7 Графические зависимости между параметрами первой формулы Эрланга

Потери являются функцией двух переменных:

Y v

P=Ev(Y )= f (v ,Y )= v v! i

∑ Y

i=0 i!

Практический интерес представляет область малых потерь: 0.001÷0.01

Поступающая нагрузка изменилась с 32.5 Эрл до 37.9 Эрл, то есть на 17%, а потери возросли в 10 раз! Это область малых потерь.

На практике приходится часто решать задачу определения числа линий по нагрузке при заданной величине потерь. Эта функция в явном виде не выражается. Решить задачу можно методом подбора.

При P=const в достаточно большом интервале изменения нагрузки
при Y >10 Эрл приближённо	V ≈α Y +β .
Перейти к оглавлению>>>	strelnikov.ws	62

Замечание 3. Область применения формулы Эрланга: а) поток — простейший; б) включение линий — полнодоступное.

	1		1
	1		1
Y =5 Эрл	2:	P=5‰	:2
Y =5 Эрл	2:	P=5‰	:2
	N=10		v
	N=10		v

Пусть N =10 источников создают нагрузку Y =5 Эрл. . Чтобы обеспечить потери, равные 0.005 ( P=5‰ ), требуется по формуле v=12 линий. Но в такой схеме одновременно может быть занято только 10 линий. Этот парадокс объясняется тем, что использована формула Эрланга для

непростейшего потока. Должно соблюдаться условие N 103 NA .

Таблицы первой формулы Эрланга приведены в следующих книгах:

1)Р. А. Аваков, М. М. Подвидз, В. Е. Родзенко - «Учебное пособие по курсовому проектированию координатных АТС», издательство ЛЭИС, 1961г;

2)Г. П. Башарин - «Таблицы вероятностей и средних квадратических отклонений на полнодоступном пучке линий», издательство ВЦ АН

СССР, 1962г;

3)«Проектирование координатных автоматических телефонных станций типа АТСК», МЭИС, 1969г.

Форма таблиц:

Y \ v:	11	12	...

5.0	008287	003441	...

5.1	009332	003950	...

...	...	...	...

Перейти к оглавлению>>>

strelnikov.ws

3.8 Обслуживание полнодоступного пучка потока от ограниченного числа источников нагрузки (формула Энгсета)

1. Постановка задачи.

Аналогично тому, как мы делали в предыдущем параграфе, определим три основных элемента математической модели:

1			1	Pi (t)=?
1			1
2	КС		2
2	КС		2
:		:		i=0,1,… ,v
N			v
N			v

Дано:

1. Коммутационная система — однозвенная, в выходы которой включён полнодоступный пучок из v линий;

2. На коммутационную систему поступает случайный ординарный и стационарный поток вызовов от N источников. Для такого потока вероятность поступления новых вызовов будет зависеть от числа обслуживаемых в рассматриваемый момент времени вызовов (от числа занятых линий в пучке).

Длительность обслуживания вызовов пусть как и прежде подчиняется показательному закону распределения с параметром

β :

F2 (t)=P(tв<t)=1−e−βt

3.В качестве дисциплины обслуживания примем обслуживание с явными потерями.

Требуется найти вероятность занятия i любых линий из общего числа v в фиксированный момент времени.

2. Вывод формулы Энгсета.

Вспомним процесс рождения и гибели — частный случай марковского процесса.

λ0

λ1

λ2

λi−1

λi

...

vi+1

Pi=λ0 λ1 … λi−1 P0

;

∑ Pi=1 .

∞

v1 v2 … vi

i=0

Перейти к оглавлению>>>

strelnikov.ws

λ0

λ1

λ2

λi−1

λi

λv−1

...

vi+1

vi для

Рассмотрим систему в стационарном режиме. Определим

λi и

рассматриваемой модели.

Обозначим через

α вероятность поступления хотя бы одного вызова от

свободного абонента на отрезке

при

t →0 (параметр свободного

источника). В состоянии системы

из

источников свободно

N −i

источников. Следовательно, вероятность поступления вызова в состоянии

системы

xi за

t :

λi=(N −i) α

, то есть λi=(N −i) α

;

Где α

— параметр свободного источника.

Вероятность освобождения одной линии за отрезок

равна:

t v1=β t

В состоянии xi

занято i

линий. Вероятность освобождения одной

линии (или первой, или второй, …, или

-той) равна:

t vi=i β t , то есть vi=i β .

Для такой модели вероятность перехода в следующее состояние зависит от предыдущего состояния, но не зависит от того, как система оказалась в этом предыдущем состоянии, то есть процесс Марковский.

Подставив в выражение для Pi

вместо

λi и vi их значения через

α и

β , получим:

λ0 λ1 … λi−1

N α ( N −1) α … [ N −(i−1)]

Pi=

P0=

P0=...

β 2 β 3 β… i β

v1 v2 … vi

N (N −1) (N −2) ... [ N −(i−1)] αi

α i

N !

...=

βi

P0=C N (β ) P0 , где

C N =

( N −1)! i!

P0 определим из условия i=1 .

i=0

Втеории массового обслуживания и ТТС часто пользуются следующим∑ P

приёмом: для простоты записи выражений длительность занятия линий выражают в единицах средней длительности занятия, то есть принимают

β1=1 . Это изменяет масштаб, но результаты от этого не изменяются.

Перейти к оглавлению>>>

strelnikov.ws

С учётом сказанного:		P	=Ci αi P		0	;
v	v	i	N			1

∑ Pi=1 →	∑CiN αi P0=1 → P0=
				v
i=0	i=0			∑ CiN αi
				i=0

Pi= vCiN αi — распределение Энгсета (немецкий учёный, 1918г.).

∑CiN αi i=0

Огибающая распределения Энгсета похожа на огибающую распределения Эрланга.

Потери при обслуживании потока от ограниченного числа источников: 1. Потери по времени по определению представляют собой долю

времени, в течение которого заняты все

линий:

αv

Pt (N )=Pv=

C N α

N −v

−1

CN −1 α

N −v

∑ CvN αv

∑

CiN −1 αi

∑

CiN −1 αi

N −i

i=0

N −i

2. Потери по вызовам —

Pв=

Cпот.

λv

C пост.

λv−1

Потери по вызовам наступают в том случае, если заняты все

линий и в это время поступают новые вызовы.

Cпот.=Pv λv t

, где

λv=(N −v) α .

t :

Математическое ожидание числа вызовов, поступивших за

Cпост.=∑ Pi λi

, где λi=(N −i) α .

i=0

Cv αv

( N −v) α

Pv λv t

∑ CiN αi

Pв=

i=0

−v) C N α

C N α

∑ Pi λi t

∑( N −i) α

∑ (N −i) C N α

i=0

∑ CiN αi

i=0

Перейти к оглавлению>>>

strelnikov.ws

Учтём следующее соотношение:						N Ci
C i	=	N !	=	N (N −1)!	=	N Ci
¿ N		(N −i)! i!		( N −i) (N −1−1)! i!		( N −i)	N −1

Отсюда — CiN −1= NN−i CiN

Разделим числитель и знаменатель выражения для P_в на N и учитывая полученное выше соотношение, получим:

	Cv αv
Pв( N )=	N −1	→ Pt (N )=Pв( N +1)
Pв( N )=	v	→ Pt (N )=Pв( N +1)
	∑ CiN −1 αi
	i=0
(так как CiN >CiN −1		, то Pн<Pв ).

3. Потери по нагрузке запишем без доказательства:

P =	Y	пост.	−Y	обсл. =	C v αv
					N −1

Yпост. N αi i=0

Вобщем случае имеет место соотношение:v∑ Ciн

Pн Pв Pt

При практических расчётах удобнее пользоваться не параметром

свободного источника

α , а математическим ожиданием и интенсивностью

нагрузки, поступающей от одного источника —

. Соотношение между α

и a

следующее:

α=

1−a

Подставим в выражение для

вместо

его значение:

CvN (

(1−a)N

CvN av (1−a)N −v

Pt=

1−a

(1−a)N

i i

N −i

∑ C N

∑

i=0

(1−a )

i=0

a (1−a)

Перейти к оглавлению>>>

strelnikov.ws

Делая аналогичные подстановки в формулы других потерь, получим формулы Энгсета:

Cv av (1−a)N −v						}
Pt=			N
Pt=			v
∑ CiN ai (1−a)N −i
i=0
		Cv		av (1−a)N −v
Pв=			N −1				, Pн Pв Pt .
Pв=			v
		∑ CNi			−1 ai (1−a)N −i
		∑ CNi			−1 ai (1−a)N −i
		i=0
		C v		av (1−a)N −v
Pн=			N −1
Pн=			v
		∑ CiN ai (1−a)N −i
		i=0
	При				N →∞ эти формулы вырождаются в формулу Эрланга,

а при N →∞ и v →∞ — в формулу Пуассона.

Формула Энгсета потерь по вызовам табулирована в книге: Лившиц Б. С, Фадлин Я. В. - «Системы массового обслуживания с

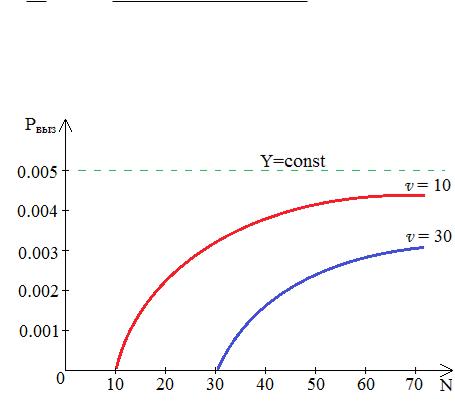
конечным числом источников», издательство «Связь», 1968г. Поступающая нагрузка Na от N источников принята равной

нагрузке Y , создаваемой простейшим потоком при Ev (Y )=const=5 ‰ .

Перейти к оглавлению>>>

strelnikov.ws

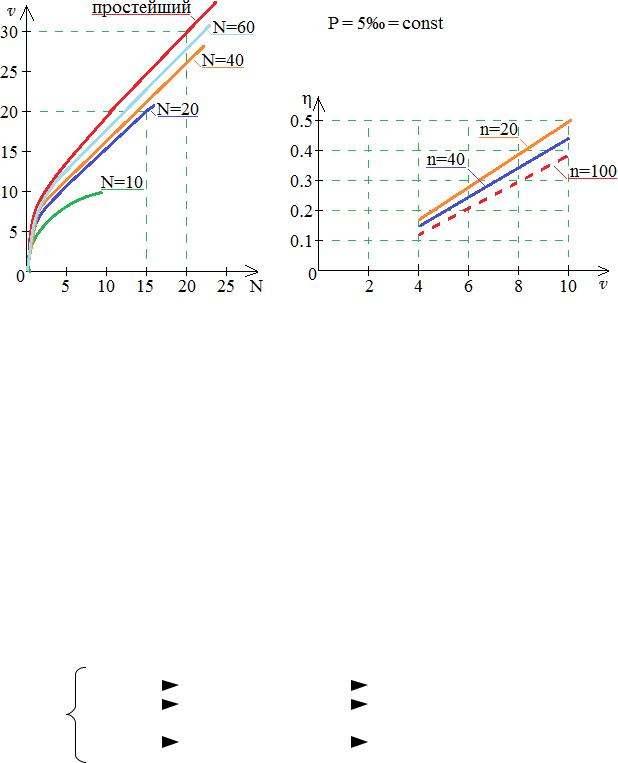
3.9 Сравнение пропускной способности полнодоступного пучка при простейшем и Энгсетовском потоках

Выводы:

1.С увеличением N одной и той же велчины Na пропускная способность полнодоступного пучка при обслуживании примитивного потока приближается к пропускной способности при обслуживании простейшего потока. Чем меньше ёмкость полнодоступного пучка линий, тем меньше указанное различие.

С возрастанием Na

увеличивается пропускная способность при

обслуживании примитивного потока по сравнению с простейшим. Это

объясняется тем, что для примитивного потока параметр потока от одного

абонента в момент его свободности равен α , а в момент занятости —

нулю. Для простейшего потока параметр потока от одного источника

считается равным α

вне зависимости от занятости либо свободности

абонента.

В практических расчётах формулой Эрланга пользуются при

N 100 .

При

N <100 – формулой Энгсета.

Пример:

Y =5 Эрл

P 5‰

По формула Эрланга

v=12

линий.

По формуле Энгсета

v=9

линий.

Перейти к оглавлению>>>

strelnikov.ws

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.09.20192.19 Mб10teoria_torgi.doc
#
15.03.20152.99 Mб178tom1_2005_web.pdf
#
13.07.201947.57 Кб9transfer.rtf
#
29.12.2019505.86 Кб0ts_bum_lek_003+.doc
#
10.01.2020193.22 Кб0TTD_lab__4.docx
#
15.03.20151.11 Mб87TT_v2.0.pdf
#
15.03.2015676.43 Кб1828tvims_3.pdf
#
21.04.20194.04 Mб44TYeMA_1.doc
#
03.01.20202.08 Mб0UchbnoePosobieV14 - p2.doc
#
28.04.20192.56 Mб30Uch_posobie_po_MSS.doc
#
15.03.201538.35 Кб101Unit_1_Convergence_in_Telecoms_and_IT.docx