
- •Введение
- •Предмет и задачи теории телетрафика
- •Раздел 1
- •Потоки вызовов
- •1.1 Способы определения и задания потоков вызовов
- •1.2 Основные свойства потоков вызовов
- •1.3 Основные характеристики потоков вызовов
- •1.4 Простейший поток вызовов и его свойства
- •1.5 Математическое ожидание
- •1.7 Длительность обслуживания. Поток освобождений
- •1.8 Простейшая классификация потоков
- •Раздел 2
- •Телефонная нагрузка
- •2.1 Определения телефонной нагрузки
- •2.2 Основные параметры нагрузки
- •2.3 Концентрация телефонной нагрузки
- •2.4 Способы распределения нагрузки
- •и доверительном интервале
- •Раздел 3
- •Методы расчёта пропускной способности полнодоступных включений в однозвенных коммутационных системах с потерями
- •3.2 Дифференциальные уравнения Эрланга
- •3.3 Стационарный режим. Распределение Эрланга
- •3.5 Рекуррентная формула Эрланга
- •Раздел 4
- •Системы с ожиданием
- •4.1 Обслуживание простейшего потока вызовов полнодоступным пучком с ожиданием при показательном распределении длительности занятия
- •4.2 Системы с ожиданием при постоянной длительности обслуживания
- •4.3 Расчёт пропускной способности управляющих устройств
- •4.4 Комбинированная система обслуживания Ограниченное число мест для ожидания
- •4.5 Расчёт систем с повторными вызовами
- •Раздел 5
- •5.1 Основные характеристика НПД включений
- •5.2 Типы НПД включений и выбор их структуры
- •5.3 Идеально-симметричные неполнодоступные схемы
- •5.4 Формула Эрланга для идеальной НПД схемы (третья формула Эрланга)
- •5.5 Приближённые методы расчёта пропускной способности НПД схем
- •Дополнительные и справочные материалы
- •Функции плотности и распределения вероятностей
- •Теорема Бернулли. Распределение Пуассона
- •Подробное доказательство второй формулы Эрланга
Курс «Теория телетрафика»
Лекций — по плану 52 часа. Экзамен. Упражнения — 50 часов.
Курсовой проект — с оценкой в этом семестре.
Литература:
1.Основная:
1.1.Ю. Н. Корнышев, А.П. Пшеничников, А. Д. Харкевич - «Теория телетрафика» - учебник для вузов. Москва, издательство «Радио и связь», 1996г, 272 с.
2.Дополнительная:
2.1.Ю. Н. Корнышев, Г. Л. Фань - «Теория распределения информации» - Москва, издательство «Радио и связь», 1985г, 184с.
2.2.М. А. Шнепс - «Системы распределения информации. Методы расчёта» - Москва, издательство «Связь», 1979г.
Введение
Предмет и задачи теории телетрафика
Теория телетрафика (от греческого Tele – далеко и английского Traffic – движение) — движение, нагрузка, то есть движение и обслуживание потоков сообщений в коммутируемых сетях.
Предметом теории телетрафика является количественная сторона процессов обслуживания потоков сообщений в системах коммутации. Под системой коммутации будем понимать ступень искания, станцию или сеть. Как и любая другая математическая теория, теория телетрафика оперирует не с самими системами коммутации, а с их математическими моделями. Математическая модель системы телетрафика включает следующие три основных элемента:
1.Входящий поток вызовов — П;
2.Схему системы коммутации — S;
3.Дисциплину обслуживания потока вызовов — Д.
Перейти к оглавлению>>> |
strelnikov.ws |
1 |
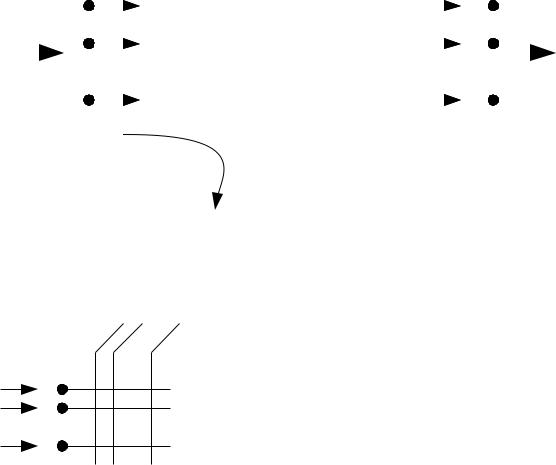
Схема математической модели: |
|
|
|
|
|
|
||||||
|
|
Входы: |
|
Выходы: |
|
|||||||
1 |
|
|
|
|
1 |
|
|
|
||||
Схема |
|
|
||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
системы коммутации |
|
|
|
|
П обсл. |
||||
|
|
|
. |
|
. |
|
|
|
|
|||
|
|
|
|
v |
||||||||
П пост. n : |
S |
: |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
П пот.
Простейшая система коммутации — коммутатор n х v.
Схема коммутатора на n входов и v выходов:
1 
 ...
... 
1
Системы коммутации изучаются в одноимённом курсе и подразделяются на: полнодоступные и неполнодоступные; однозвенные и многозвенные.
Поток вызовов — это последовательность однородных событий, наступающих через некоторые интервалы времени.
Дисциплина обслуживания характеризует взаимодействие потока вызовов
ссистемой коммутации. Дисциплина обслуживания характеризуется:
•Способами обслуживания вызовов (с потерями, с ожиданием, комбинированные);
•Порядком обслуживания вызовов (в порядке наступления, в случайном порядке и др.);
•Режимами искания выходов схемы (свободное, групповое, индивидуальное);
•Законами изменения длительности обслуживания вызовов (показательный закон, постоянная или произвольная длительность обслуживания);
•И другими характеристиками (наличие приоритетов, ограничений и т. д.)
Перейти к оглавлению>>> |
strelnikov.ws |
2 |
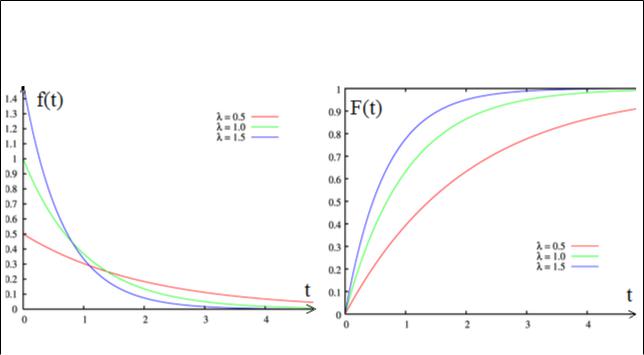
Подробнее о функциях плотности и распределения вероятностей >>>
В научной литературе для компактной записи математических моделей используются обозначения, предложенные Д. Кендаллом. Математическую модель обозначают последовательностью символов:
1.Первый символ обозначает функцию распределения промежутков между вызовами (то есть поток вызовов);
2.Второй символ — функцию распределения длительности обслуживания вызовов;
3.Третий символ — схему;
4.Последующие символы характеризуют дисциплину обслуживания.
Распределение обозначаются следующими символами:
•M — показательное (экспоненциальное) распределение;
•Е — эрланговское (гамма) распределение;
•Д — регулярное (детерминированное — латинское determinave – определять, обуславливать) — поток с постоянными интервалами между вызовами;
•G — произвольное распределение.
Основные свойства распределений:
Показательное распределение:
Плотность вероятности |
Функция распределения |
f (t)=β e−β t |
F (t)=1−e−β t |
|
|
Перейти к оглавлению>>> |
strelnikov.ws |
3 |
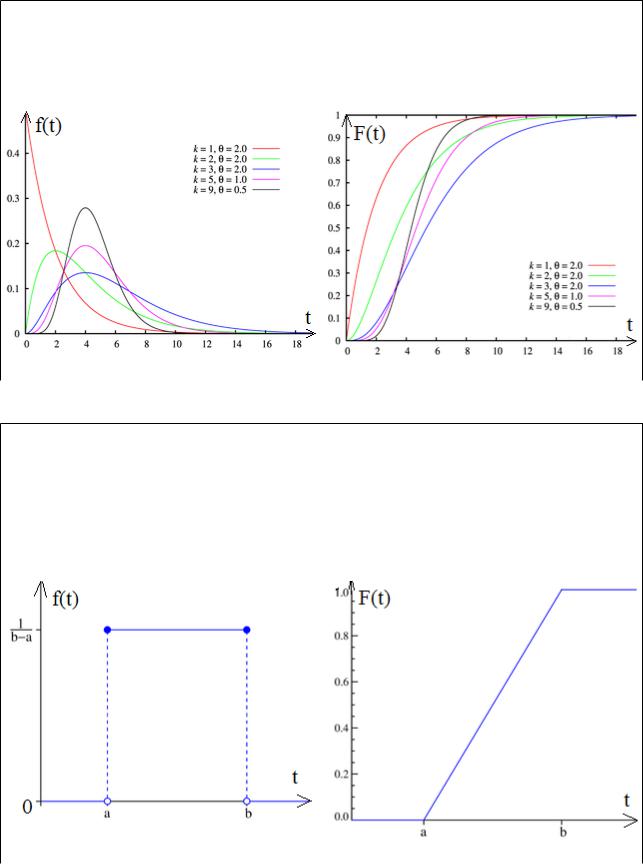
Эрланговское распределение
Плотность вероятности |
Функция распределения |
||||
f (t)=t |
k −1 |
e−x/θ |
F (t)= |
γ(k ,t /θ) |
|
|
|
|
Γ(k) |
||
Γ(k ) θk |
|||||
|
|
|
|
|
|
Регулярное распределение
Плотность вероятности |
Функция распределения |
|||||
1 |
|
0 |
, |
t<a |
||
f (t)= |
|
, a t b |
F (t)={ |
t−a |
|
|
b−a |
|
|
||||
{0 , t<a , t>b |
|
,, |
ta bt<b |
|||
b−a1 |
||||||
|
|
|
|
|
|
|
Перейти к оглавлению>>> |
strelnikov.ws |
4 |
Для многомерного случая над символами ставятся стрелки, например:
M
Пример записи математической модели: M/M/S. Такая запись обозначает, что на произвольную схему S поступает поток вызовов с показательной функцией распределения промежутков между вызовами (первый символ М). Функция распределения длительности обслуживания — показательная (второй символ М). Если схема системы коммутации представляет собой полнодоступный пучок из v линий, то вместо S пишется v.
Построение математической модели, адекватно отражающей реальную систему коммутации, является не тривиальной задачей. Правильно построить математическую модель — это уже половина дела.
Основная цель теории телетрафика заключается в разработке методов оценки качества функционирования систем коммутации.
Основными задачами теории телетрафика являются задачи анализа, синтеза и оптимизации.
Задача анализа заключается в отыскании функциональной зависимости между качеством обслуживания P, параметрами входящего потока вызовов П, схемы S и дисциплины обслуживания D. P= f ( П , S , D)
Задача синтеза заключается в отыскании структурных параметров коммутационных систем при заданных потоках, дисциплине и качестве обслуживания. S= f ( П , P , D)
Задача оптимизации заключается обычно в минимизации объёма оборудования систем коммутации при заданных потоках, дисциплине и качестве обслуживания. K (S )= f ( П , P , D)→ min
Мы в курсе будем заниматься в основном задачами анализа.
Основным математическим аппаратом теории телетрафика является теория вероятностей, математическая статистика и комбинаторика.
Основоположником теории телетрафика является датский учёный Агнер Краруп Эрланг (1878 — 1929, с 1908г работавший в копенгагенской телефонной компании). Большой вклад в теорию внесли советские учёные, особенно советский математик А. Я. Хинчин (1894 — 1959). С другими учёными мы познакомимся в процессе изучения курса.
Перейти к оглавлению>>> |
strelnikov.ws |
5 |
