11.2. Методы повышения достоверности в однонаправленных системах

11.2.1.Однонаправленные системы с многократным повторением сообщений

а) Системы передачи с простым кодом

В системах передачи дискретных сообщений, передаваемых комбинациями простого кода, находят применение 5, 6, 7,8 - элементные коды.

В обычном режиме (без повторения) относительная скорость передачи данных равна:

R_о = 1,

а вероятность ошибок в знаке сообщения, поступающему к пользователю, равна:

Р_ош=Р(≥1, n).

Расчетные формулы для Р_ош имеют вид:

- для канала с независимыми ошибками: Р_ош = 1 – (1- р)ⁿ ≈ np;

- для канала с группирующимися ошибками: Р_ош = n^1-α p.

В этих формулах, как и ранее, приняты следующие обозначения:

- n – длина кодовой комбинации,

- р – вероятность ошибочного приема бита (битовая ошибка),

- α – показатель группирования ошибок по модели Л.П. Пуртова.

Таким образом, вероятность ошибки в знаке сообщения на выходе системы ПДС для различных каналов Р_ош > p , что не отвечает требованиям большинства пользователей.

Обеспечение требуемого уровня защиты от ошибок при использовании этих кодов в системах передачи данных возможно только в режиме многократного повторения. Каждая кодовая комбинация передается λ раз, где величина λ достаточно большое нечетное число. На принимающей станции выявление переданной источником комбинации производится по мажоритарному принципу, т.е. по большинству совпадения принятых значений. Возможны следующие методы анализа принятых комбинаций с целью принятия решения о переданной информации:

- решение по совпадению кодовых комбинаций (знаков сообщений),

- решение по совпадению элементов кодовых комбинаций.

Относительная скорость передачи в системах передачи данных простым кодом при λ-кратном повторении равна: R_о = 1/ λ.

Вероятность ошибки на выходе системы зависит от метода анализа принятых комбинаций.

В случае принятия решения по большинству совпадения повторяемых знаков сообщений ошибочный приём происходит в том случае, когда большинство из λ повторяемых знаков приняты с ошибками. Вероятность такого события равна:

Р_ошз =.

Здесь: - Р = Р(≥1, n) и вычисляется как было показано выше,

- С- биномиальный коэффициент.

В системе с анализом элементов решение производится по каждому из n элементов λ повторяемых знаков. Оценка производится по большинству его принятых значений в последовательности из λ повторяемых знаков.

В данном случае ошибочный приём происходит в том случае, когда большинство из λ повторяемых элементов на одинаковых позициях повторяемых знаков приняты с ошибками. Вероятность такого события равна:

Р_ошэ= .

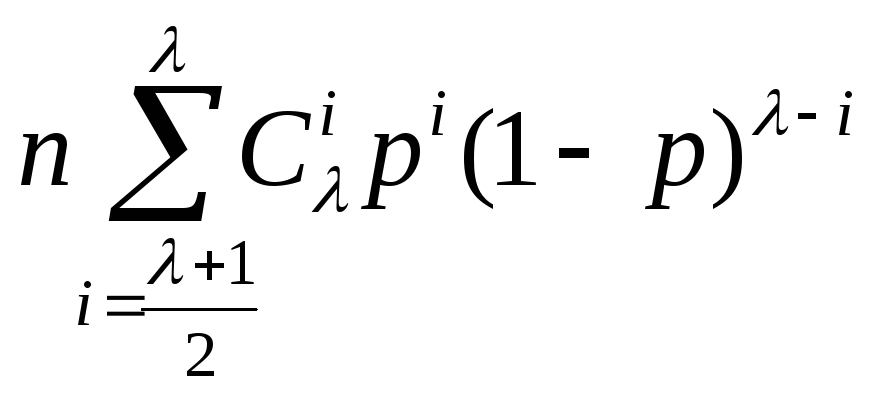Здесь р – битовая ошибка.

Представляет интерес сравнить эти методы по эффективности защиты от ошибок. Для этого возьмем отношение Р_ошз к Р_ошэ:

Р_ошз / Р_ошэ =/≈.

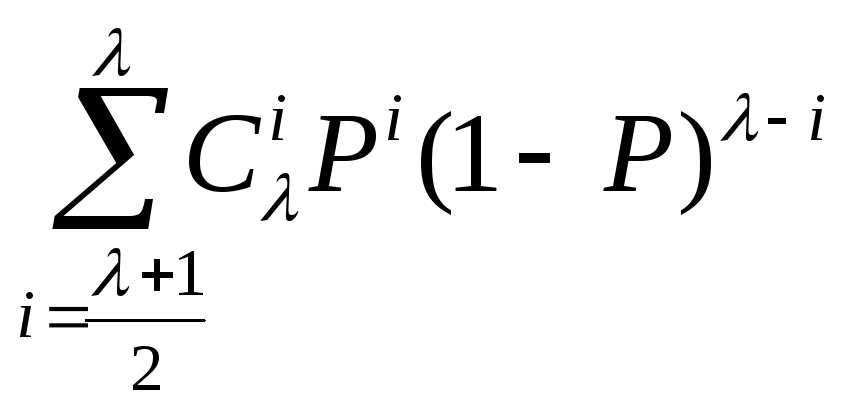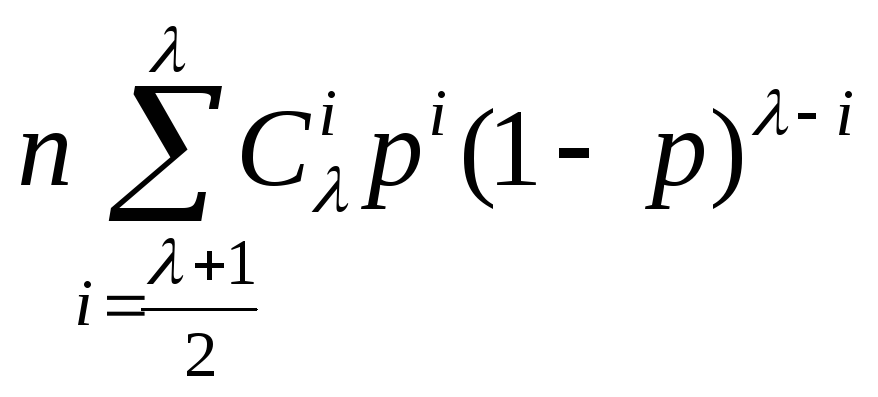При вычислении было принято Р = np и значение суммы определялось величиной первого слагаемого. Из результатов сравнения можно сделать вывод, что анализ по элементам при λ-кратном повторении передаваемой информации в nраз дает меньшую ошибку, чем анализ по знакам. Таким образом, при мажоритарной обработке поэлементный анализ предпочтительнее, так как дает больше информации об ошибках.

б) Системы передачи с обнаруживающим ошибки кодом

В однонаправленных системах возможно применение помехоустойчивых (n,k)-кодов в режиме обнаружения ошибок. При однократной передаче кодовой комбинации относительная скорость передачи равна: R_о = k/n. Вероятность необнаруженной ошибки

в принятой комбинации (n,k)-кода на выходе декодера определяется выражением:

Р_но =P(≥d, n).

Надлежащим выбором параметров (n,k)-кодов можно добиться сколь угодно малой вероятности ошибки в принимаемой кодовой комбинации. Однако, доля обнаруживаемых ошибок, равная величине Р_оо=P(≥1, n) - P(≥d, n), будет характеризовать информационные потери системы, проявляющиеся в выдаче получателю сигнала стирания вместо тех комбинаций, в которых были обнаружены ошибки.

Исправление ошибок при использовании помехоустойчивых (n,k)-кодов в режиме обнаружения ошибок возможно при многократной передаче кодовой комбинации (n,k)-кода. Существует ряд способов исправления ошибок в многократно принимаемой комбинации (n,k)-кода, обнаруживающего ошибки. Рассмотрим один из них, известный как метод последовательного замещения комбинаций с обнаруженными ошибками.

Суть метода состоит в следующем. Передатчик передает комбинацию (n,k)-кода λ раз.

При обработке принятой комбинации каждого повтора в декодере возможно три исхода:

- правильный прием с вероятностью Р_пр = 1 - P(≥1, n),

- прием с необнаружением ошибок с вероятностью Р_но =P(≥d, n),

- прием с обнаружением ошибок с вероятностью Р_оо = 1 - Р_пр - Р_но = P(≥1, n)- P(≥d, n).

В случае правильного приема или приема с необнаружением ошибок первая принятая комбинация выдается с выхода декодера к пользователю и обработка последующих повторов данной комбинации не производится. Вероятность ошибки в этом случае равна Р_ош1 = Р_но.

Если же в первой принятой комбинации обнаружены ошибки, то в декодере анализируется принятая комбинация второго повтора. Здесь возможны те же три исхода с теми же последствиями: при правильном приеме или приеме с необнаружением ошибок комбинация второго повтора выдается с выхода декодера к пользователю и обработка последующих повторов данной комбинации не производится. Вероятность ошибки в этом случае равна Р_ош2 = Р_но + Р_оо Р_но.

Если же в комбинации второго повтора обнаружены ошибки, то в декодере анализируется принятая комбинация третьего повтора. Исходом этого анализа может быть либо выдача принятой комбинации пользователю, либо переход к анализу кодовой комбинации четвертого повтора. Вероятность ошибки в этом случае равна

Р_ош3 = Р_но + Р_оо Р_но. + РР_но= Р_но .

В том случае, когда обнаружение ошибок имеет место во всех λ повторах, то принятая комбинация выдается пользователю с вероятностью ошибки

Р_ошλ = Р+ Р_но .

Относительная скорость передачи данных в рассматриваемой системе не зависит от того, на каком повторе принято решение о выдаче принятой комбинации пользователю и равна: R_о= .

Анализируя слагаемые, входящие в выражение для Р_ошλ , можно сделать вывод о количестве необходимых повторов в данном методе защиты от ошибок. С увеличением

λ значение Р_ошλ определяется величиной Р_но и не может стать меньше этой величины.

Поэтому число повторов λ можно ограничить таким значением, при котором Р≤ Р_но.

Рекомендуемое значение повторов λ= 2,3.