6.4. Коды Боуза-Чоудхури-Хоквингема (бчх).

Определение корректирующих свойств циклических кодов, предназначенных для коррекции многократных ошибок, сводится к определению минимального кодового расстояния этих кодов или к установлению максимальных значений кратностей гарантийно исправляемых или обнаруживаемых ошибок.

Следующие две теоремы позволяют определить важнейший класс двоичных циклических кодов и установить корректирующую способность этого класса циклических кодов.

Теорема 6.1. Для любых значений l и t существует циклический код длины , исправляющий все ошибки кратностиt и менее и содержащий не более проверочных символов.

Формулировка этой теоремы заимствована из [1]. Следует уточнить, что при произвольном lпараметрt не может быть любым. Его максимальное значение не должно превышать числа(n-1)/2, т.е.t≤2^r-l-1.

Пример 6.7. Найти циклические коды длиныn=31, исправляющие ошибки кратностиt=1, 2, 3.

Определяем l. Так как 31=2⁵-1, тоl=5. Находим количество проверочных элементов для заданных значенийt:

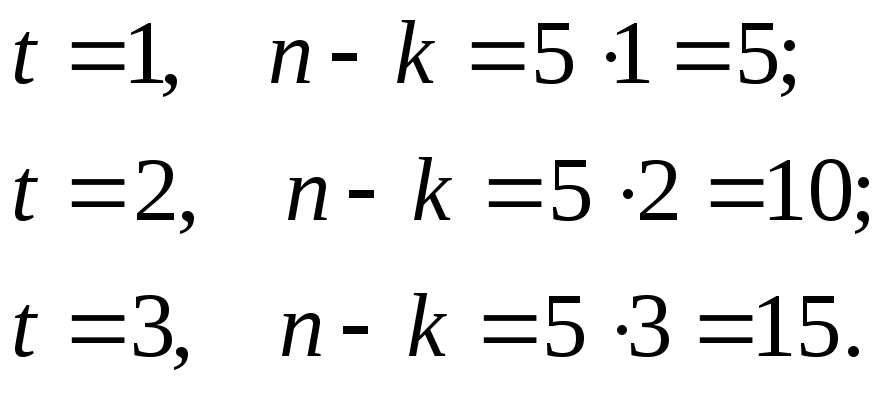
Таким образом, искомые коды (31, 26), (31, 21) и (31, 16).

Следует заметить, что теорема 6.1 определяет лишь существование кодов с известными корректирующими свойствами. Построение же кодов, действительно обладающих этими свойствами, зависит от правильного выбора порождающего многочлена.

Теорема 6.2. Если среди корней порождающего многочлена циклического (n, k) – кода имеются корни вида то минимальное расстояние этого кода равно, по меньшей мере,d.

Циклические коды, удовлетворяющие этим теоремам получили название кодов Боуза-Чоудхури-Хоквингема,или кодов БЧХпо фамилиям их авторов.

Коды БЧХ - обширный класс кодов, предназначенный в первую очередь для исправления многократных ошибок. Коды БЧХ включают в свой состав коды Хэмминга и обобщают их на случай t>1.

Коды БЧХ существуют над полем GF(q), гдеq≥2. При этом Теорема 6.1., сформулированная для случаяq=2, может быть обобщена дляq>2. Однако, это обобщение выходит за рамки настоящего учебного пособия. Теорема 6.2. справедлива дляq≥2и будет использована при изучении недвоичных циклических кодов.

Изучение кодов БЧХ является основой для понимания других классов циклических кодов.

6.5. Выбор порождающего многочлена для кода бчх

а) Порождающий многочлен для (n, n-1) – кодов.

В примере 6.3 было показано, что один из возможных кодов длины 7 есть (7,6) – код с . Покажем, что этот код образуется на основе проверки на четность всех информационных элементов кодовой комбинации. Для этого определим проверочный многочленh(x)и построим проверочную матрицу (7,6) – кода. Находим

и

,

т.е. действительно (7,6)-код с является кодом с одной проверкой на четность по всем элементам кодовой комбинации. Распространим результат рассмотренного примера на общий случай.

В общем случае (n,n-1) – кода при любом значенииnпроверочный многочлен находится как. Так как двучленыиимеют общий кореньx=1, то справедливо

,

т.е. многочлен порождает (n,n-1) – код длиныnс проверкой на четность по всем элементам.

б) Порождающий многочлен для общего случая циклического кода

Теорема 6.2 позволяет осуществить выбор порождающего многочлена для БЧХ кода и по его корням определить корректирующие свойства этого кода.

Пример 6.8.Порождающий многочлен кода (7,4) из примера 6.6 имеет своими корнямии. Определим корректирующие свойства этого кода.

Находим максимальное число последовательных степеней корней порождающего многочлена. Это элементы и. Здесь=1, а, откудаd = 4-= 3.

Использование теоремы 6.2 для выбора порождающих многочленов циклических кодов, а также для определения корректирующих свойств циклических кодов предполагает знание корней многочленов, которые могут быть выбраны в качестве порождающих многочленов кодов. Поскольку порождающий многочлен циклического (n,k) – кода должен быть делителем, то для нахождения всех возможных кодов длиныn, выбора порождающих многочленов и установления их корректирующих свойств необходимо знание сомножителейи их корней.

Таблицы разложения с указанием корней неприводимых сомножителей в виде степенейи циклические коды, построенные на их основе, приведены в [2, 3].

Таблица кодов БЧХ с n=7÷1023 приведена в Приложении к настоящему пособию.

Пример 6.9.Найти порождающие многочлены для кодов длиныn= 31 из примера 6.7. Из приложения 1 [2] находим неприводимые сомножителии последовательности их корней:

Сомножитель	его степень	последовательность степеней корней
	1	0=31
	5	1 2 4 8 16
	5	3 6 12 24 17
	5	5 10 20 9 18
	5	7 14 28 25 19
	5	11 22 13 26 21
	5	15 30 29 27 23

Для кода (31,26) с t = 1 в качестве порождающего многочлена можно взятьтак как корни каждого из них содержат по две последовательные степени, а значит, по теореме 5.2 эти коды имеютd_min= 3.

Для кода (31,21) порождающий многочлен должен иметь степень 10. Он может быть получен, как произведение двух неприводимых многочленов пятой степени

В соответствии с теоремой необходимо, чтобы порождающий многочлен имел среди своих корней 4 последовательных степени. Этому требованию удовлетворяют, например, многочлены и. Для кода (31,16) в качестве порождающего многочлена целесообразно выбрать многочленыи, у которых среди корней имеются элементыисоответственно, что обеспечивает требуемые корректирующие свойства кода.

в) Улучшение корректирующих свойств циклических (n, k) – кодов умножением порождающего многочлена на .

Для кодов с нечетным значением минимального кодового расстояния последнее может быть увеличено на единицу умножением порождающего многочлена g(x)на. Выше было показано, что использование двучленав качестве порождающего многочлена дает код с проверкой на четность. Умножение порождающего многочлена некоторого циклического кода наприводит к введению дополнительной проверки на четность в этом коде по всем кодовым элементам. Если код имеет четное значениеd_min, то дополнительная проверка на четность не изменит его величины, т.к. введение в проверочную матрицу строки из одних единиц не изменит минимального числа линейно не зависимых столбцов.

Если же d_minнечетное, то введение в проверочную матрицу строки из одних единиц приводит к увеличению минимального числа линейно зависимых столбцов на один.

Пример 6.10.Рассмотрим проверочную матрицу кода (7,3) из примера 6.3. Если в качестве порождающего многочлена выбрать, проверочным многочленом будет

Матрица проверок для этого кода имеет вид

Сложив 1, 2 и 4-ю строки и записав результат вместо 4-й строки, получим проверочную матрицу этого же кода в следующем виде

Проверочная матрица кода (6,3) с dmin=3состоит из проверочной матрицы укороченного кода (7,4) (обозначена пунктиром), к которой добавлена строка, обеспечивающая проверку на четность по всем элементам кодовой комбинации. Минимальное кодовое расстояние равно 4 (линейно зависимы, например, 1, 2, 3 и 6-й столбцы).

г) Выбор порождающих многочленов для укороченных кодов

Как и все групповые коды, циклические коды могут подвергаться укорочению. При этом порождающий многочлен остается тем же, что и у исходного кода. Так как в результате укорочения уменьшается длина кодовой комбинации, то не все циклические сдвиги кодовой комбинации в укороченном (n-i,k-i) – коде будут кодовыми комбинациями. В силу этого обстоятельства, укороченные циклические коды называют псевдоциклическими. Методика построения кодовой комбинации для укороченного циклического кода остается той же, что была рассмотрена в разделе 6.2, т.е. каждая кодовая комбинация укороченного циклического кода кратна порождающему многочленуg(x), и корректирующие свойства укороченного циклического кода полностью определяются корнямиg(x). Для укороченных кодов проверочные многочленыh(x)не определяются, а матрицы проверок строятся на основе порождающих матриц. Выбор порождающих многочленов для псевдоциклических кодов наиболее рационально производить на базе кодов, построенных по теореме 6.1. При этом можно при заданной абсолютной избыточности обеспечить требуемые корректирующие свойства и сохранить скорость передачи кода близкой к требуемой.

Пример 6.11. Выбрать порождающий многочлен для кода (50,35) с.

Выбор производим по необходимому числу избыточных элементов n-k=15. Так как требуется обеспечить, то по теореме 6.1 принимаемt=2. Ближайшее к требуемому значение избыточных элементов достигается приl=7.

Таким образом, исходным циклическим кодов является (127,113) – код с . Этот код имеет. Следовательно, необходимо добавить еще один избыточный элемент. Для этого умножимg(x)на, т.е. вводим проверку на четность по всем элементам. Получаем (127,112) – код с. Укорочением данного кода на 77 разрядов получаем требуемый код. Итак, в качестве порождающего многочлена для кода (50,35) можно взять. Данный код имеет.