6.7.2. Линейные переключательные схемы, используемые в кодирующих и декодирующих устройствах циклических кодов

Основное оборудование кодирующих и декодирующих устройств циклических кодов составляют схемы деления и умножения многочленов – линейные переключательные схемы[1].

Линейные переключательные схемы представляют собою соединения элементов трех видов:

- элемент единичной задержки (ячейка памяти, разряд регистра);

- сумматор по модулю 2;

- устройство умножения на постоянную величину С.

Обозначение используемых элементов изображено на рис. 6.1.

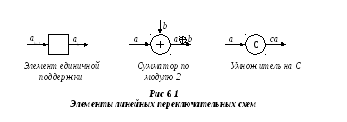
Элемент единичной задержкиимеет один вход и один выход. Символна выходе совпадает с символом, появившимся на входе в предыдущий момент времени.

Сумматор по модулю 2имеет два входа и один выход. Символ на выходе равен сумме по модулю 2 входных символов.

Умножение на постоянную величину для значения С=1 равносильно наличию связи, а для значения С=0 – отсутствию связи.

Будем полагать, что операции, выполняемые с помощью сумматора и умножителя, осуществляются мгновенно. Все изменения в линейных переключательных схемах также происходят мгновенно в момент прихода тактовых импульсов. Вход и выход предполагаются последовательными, т.е. входная последовательность состоит из двоичных символов, подаваемых ко входу по одному символу в момент поступления каждого тактового импульса. Если в качестве входной или выходной последовательности рассматривается многочлен, то на вход или с выхода поступают только коэффициенты, начиная с коэффициентов при старших степенях. Так многочленбудет подаваться на вход или появляться на выходе в виде последовательности из (n+1)-го двоичного элемента, начинающейся с. По следующему тактовому импульсу появится, еще через тактf_n-2 и т.д.

а) Схемы для умножения многочленов

На рис. 6.2 изображения схема, осуществляющая умножение любого многочлена, подаваемого на вход, например, на фиксированный многочлен.

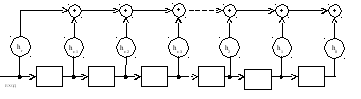
Рис 6.2

Схема для умножения на многочлен

h(x) = h₀ + h₁x + … + h_r-1x^r-1 + h_rx^r

В исходном состоянии ячейки памяти регистра содержат нули. На вход поступают коэффициенты многочлена а(х), начиная с коэффициентов высших порядков, после чего следуетrнулей. Произведение равно:

Когда по первому тактовому импульсу на входе появляется первый коэффициент многочленаа(х), то на выходе появляется первый коэффициент произведения, равныйизаписывается в первый разряд регистра. В этот момент все остальные разряды регистра сдвига содержат нули. Спустя единицу времени по второму тактовому импульсу на входе появляется. Как видно из рис. 6.2 выход по второму тактовому импульсу равен, т.е. величине второго коэффициента в произведении. К моменту появления третьего коэффициента на входе () разряды регистра содержат элементыВыход по третьему такту равент.е. третьему коэффициенту произведения. Дальнейшие операции производятся аналогичным образом.

По (r+k)-му такту регистр сдвига содержит элементы 0, 0, …, 0,а₀, а выход равен, т.е. предпоследнему коэффициенту произведения. После (r+k+1)-го такта в регистре остаются одни нули, а на выходе появляется- последний коэффициент произведения, так что произведение получено полностью.

Другая схема для умножения многочленов показана на рис.6.3.

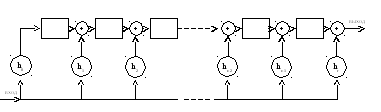
Рис 6.3

Схема для умножения на многочлен

h(x) = h₀ + h₁x + … + h_r-1x^r-1 + h_rx^r

В этой схеме коэффициенты произведения формируются в регистре сдвига. После того, как по первому тактовому импульсу символ поступил на вход, выход стал равным, т.е. коэффициенту при, а в разрядах регистра записались элементы. По второму тактовому импульсу на вход подаетсявыход становится равным, т.е. коэффициенту при, а разряды регистра содержат элементы. По третьему тактовому импульсу на вход поступаети выход равен- коэффициенту при. Дальнейшие операции производятся аналогичным образом.

б) Схемы для деления многочленов.

Схема для деления многочлена произвольной степени пна многочленпоказана на рис.6.4. Схема представляет собою регистр сдвига с обратными связями. Обратные связи соответствуют виду многочленаg(x). В исходном состоянии ячейки регистра содержат нули. Делимый многочленподается на вход схемы в течение (n+1) такта. Выход схемы деления в течениеrпервых тактов принимает значения, равные 0. Когда первый входной символпо (r+1)-му тактовому импульсу выйдет из регистра, то на выход схемы поступит старший коэффициент частного, который в рассматриваемом двоичном случае примет значение. При этом в последний разряд регистра будет записан символ, в предпоследний, и т.д., т.е. содержимое разрядов регистра будет соответствовать коэффициентам при степенях отдомногочленагде суммирование осуществляется по модулю 2. Для каждого последующего (r+j)-го этапа деления содержимое разрядов регистра сдвига определяется коэффициентами при степенях отдомногочлена, гдеq_i– символ, поступающий на выход схемы. После (n+1)-го такта работы схемы на выходе появится частное от деленияq(x), а в ячейках регистра будет записан остаток от деления.

Пример 6.14. Построить схему для деления на многочлен. Регистр должен содержать число ячеек, равное степениg(x), т.е. 3. Обратные связи должны соответствовать коэффициентам приxⁱ:

.

Сумматор по модулю 2 включается на входе и в точке подключения обратной связи g₁. Схема, соответствующая рассматриваемому случаю представлена на рис. 6.5. На этом же рисунке показана работа схемы при делении многочлена. В результате деления получено частноеи остаток. Для того, чтобы установить соответствие между работой схемы и процессом деления многочленаd(x) на многочлен q(x)рассмотрим делениена.

+

Содержимое регистра по 4-му такту

+

Содержимое регистра по 5-му такту

0 0 0 0

Содержимое регистра по 6-му такту

Остаток первого шага деления содержится в разрядах регистра после выхода первого элемента частного к выходу схемы (4-й такт). Остаток второго шага делениясодержится в разрядах регистра после вывода второго элемента частного к выходу схемы (5-й такт). Остаток от делениясодержится в разрядах регистра после вывода последнего элемента частного (6-й такт).

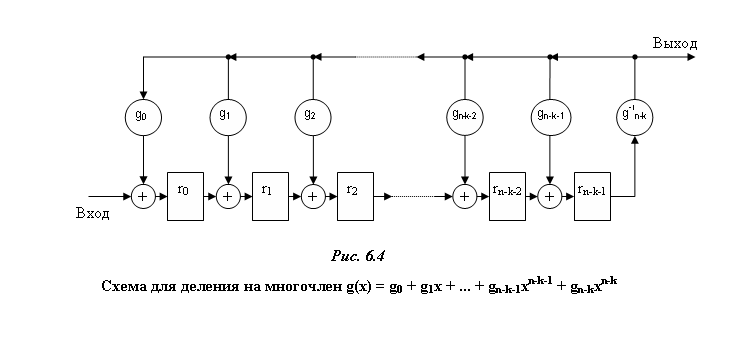
g₀ +g₁x+….+g_n-k-1 x^n-k-1+g_n-kx^n-k

Такты	Вход	Содержимое регистра			Обратная связь	Выход
		r0	r1	r2
0	-	0	0	0	0	-
1	0∙x5	1	0	0	0	0∙x6
2	0∙x4	0	1	0	0	0∙x4
3	0∙x3	0	0	1	0	0∙x3
4	0∙x2	1	1	0	1	1∙x2
5	1∙x1	1	1	1	0	0∙x1
6	1∙x0	0	0	1	1	1∙x0

Остаток r(x)= x²

Работа схемы деления на многочлен g(x)=1+x+x³ при подаче на входd(x)=1+x+x5

в) Схемы для одновременного умножения и деления многочленов

С

хема, с помощью которой можно производить сначала умножение на многочленh(x), а затем деление на многочлен g(x), изображена на рис. 6.6. Как видно из рисунка, она получена комбинированием схемы умножения, изображенной на рис 6.3 и схемы деления, изображенной на рис. 6.4. При построении схемы предполагается, что степень многочленаh(x) не превосходит степениg(x).

г) Схемы для решения рекуррентных соотношений

На рис. 6.7. изображена схема для решения рекуррентных соотношений вида или, что то же самое.

Эта схема предназначена для вычисления величины по значениюkпредыдущих коэффициентов для всех возможных многочленов степениn-1, ортогональных некоторому многочленуh(x)степениk. Для циклического (n, k) – кодаh(x)– проверочный многочлен кода. Исходные величиныпомещаются в разряды регистра. Затем осуществляются последовательные сдвиги, каждый из которых сопровождается выводом с выхода схема элементов, соответствующих решению указанных рекуррентных уравнений. После первого сдвига на выход поступает элемент, содержимое разрядов регистра сдвигается на одну единицу вправо, а в ячейкупоступит значение коэффициента, которое в соответствии со схемой рис. 6.7 должно быть равно сумме произведений коэффициентов, записанных во всех остальных разрядах регистра на значения обратных связей, подключенных непосредственно к выходам разрядов регистра, т.е.

,

что в точности соответствует значению , полученному из рекуррентного соотношения.

Аналогично можно показать формирование и всех остальных решений. В результате первых kсдвигов на выход схемы поступит содержимое разрядов регистра в исходном состоянии. Значение коэффициентапоявится на выходе схемы в результате (k +1)-го сдвига, значение- в результате (k +2)-го сдвига и т.п. Поскольку для каждого значения исходных символов решение однозначно, то по последнимkрешениям сформируется и запишется в регистр, затеми т.д., т.е. схема будет генерировать решение рекуррентного уравнения непрерывно с периодом, равнымn-1. Максимальное значение решений, т.е. максимальный период последовательности, можно определить из следующих соображений. Каждому решению соответствует свое вполне определенное значение разрядов регистра сдвига, следовательно, возможное число решений определяется числом различных состояний регистра. Так как каждая ячейка может характеризоваться двумя состояниями (запись нуля или единицы), а число ячеек в регистре равноk, то максимальное значениеnравно2^k,а максимальный период последовательности равен2^k -1и минимальный период равенk. В тех случаях, когда схема для решения рекуррентных соотношений генерируетпоследовательность с максимальным периодом, ее называютгенератором последовательности максимальной длины. В силу того, что многочленh(x)степениk, по которому стоится схема генератора последовательности максимальной длины, должен быть сомножителем двучленаприи не может быть сомножителем никакого двучлена с меньшим значениемп(т.к. период равен 2^k-1), тоh(x)должен быть неприводимым сомножителеми не должен быть сомножителем двучленов меньших степеней, т.е. должен принадлежать показателюп. Поскольку последовательности максимальной длины соответствует2^k -1различных состояний регистра сдвига (все возможные векторы длиныk, кроме чисто нулевого), то для генерирования последовательности максимальной длины в качестве исходного состояния может быть взято любое, кроме чисто нулевого. Обычно для этой цели в младший разряд регистра предварительно записывают “1”. Некоторые из неприводимых многочленов, по виду которых строятся обратные связи в регистре, приводятся в таблице 6.3 дляп=2+15.

Таблица 6.3

Число ячеек регистра	Неприводимый Многочлен	Вид обратной связи	Длина периода
2			3
3			7
4			15
5			31
6			63
7			127
8			255
9			511
10			1023
11			2047
12			4095
13			8191
14			16383
15			32767

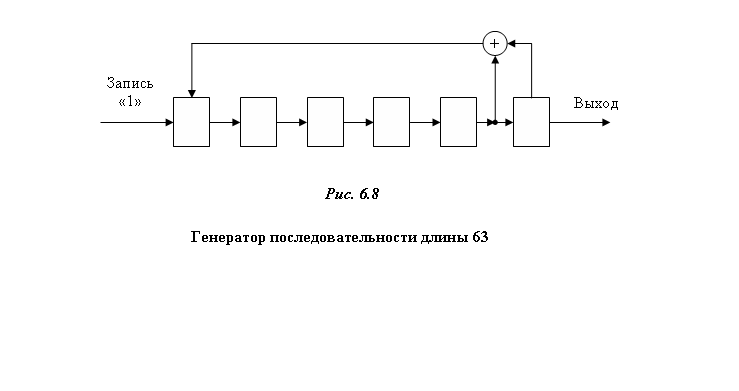
Для примера на рис.6.8 приведена структурная схема генератора последовательности максимальной длины, построенной на основе .

Число ячеек регистра сдвига равно степени h(x), т.е шести. Число сумматоров по модулю 2 на единицу меньше числа знаков “+” в записи многочленаh(x), т.е. один. Обратные связи определяются ненулевыми коэффициентами многочлена

д) Схема генератора поля Галуа GF(2^m)

Регистр сдвига с обратными связями, изображенный на рис. 6.4, реализующий деление любого многочлена на многочлен g(x)степениn-k=m, после завершения деления содержит остаток от деления

r(x) = r₀x⁰+r₁x¹+r₂x²+…+r_m-1x₀^m-1.

Он может быть представлен в виде последовательности длины m-(r₀, r₁, r₂, .. ,r_m-1)

Многочлен r(x)является представителем классов вычетов многочленов по модулю многочленаg(x). При этом каждый класс вычетов содержит либо 0, либо многочлен степениm-1и менее. Ноль является элементом идеала, а все многочленыr(x)степениm-1и менее принадлежат различным классам вычетов. Общее число классов вычетов вместе с идеалом равно 2^m.

В том случае, когда многочлен g(x)– неприводим, множество{r(x)}с коэффициентамиr_iиз поляGF(2)образует поле ГалуаGF(2^m).Как известно ненулевые элементы этого поля образуют циклическую группу

α⁰, α¹,…,α^2m-2,α^2m-1=α⁰,

где α -класс вычетов, содержащий r(x) = x, т.е. кореньg(x)и примитивный элемент поля.

Определим, каким образом можно преобразовать схему рис 6.4 в генератор элементовполя GF(2^m).В схеме деления наg(x)каждый из остатковr(x)может быть получен в результате подачиxⁱна вход схемы и осуществления процедуры деления в течениеiтактов, т.е. остаток от деления появится точно наi- м такте.

Этот результат можно получить, если в схеме деления убрать вход, а цепь обратной связи подать непосредственно на вход ячейки r₀. При этом для генерирования элементов поля как последовательности степенейαⁱв видеm-значных двоичных чисел, записанных в ячейках регистра необходимо предварительно в ячейкуr₀записать «1». В этом случае в исходном состоянии на нулевом такте работы рассматриваемой схемы как генератора элементовGF(2^m)будет записан остаток от деленияx⁰наg(x). Элемент поляαⁱпоявится в регистре наi-м такте, что соответствует подаче на вход схемы деленияxⁱна нулевом такте.

Все 2^m-1не нулевых элементовGF(2^m), будут получены за2^m-1тактов работы схемы. Доm-1такта работы схемы включительно регистр будет содержать в своих ячейках только одну единицу иm-1 нулей. Наm-м такте содержимое регистра станет равнымg'(x)=g(x)+x^m, гдеg'(x)-многочлен, состоящий из всех слагаемыхg(x), кроме слагаемого старшей степениx^m.В силу того, чтоg(x)принадлежит идеалу, т.е.{g(x)}={0},получаемg^’(x)=x^m.

Продолжая сдвиги, получим, что на m+1такте содержимое ячеек регистра будет соответствоватьxg(x), т.е. подаче на вход схемы деления на нулевом тактеx^m+1и т.д. Так будет продолжаться до тех пор, пока содержимое ячеек регистра не станет эквивалентным подаче на вход схемы деленияxⁿ. Это состояние регистра соответствуетα⁰=1,т.к.xⁿ=1( см.6.1). В силу того, что многочленg(x)примитивен, он принадлежит показателюn=2^m-1. Это означает, что до возвращения в состояниеα⁰=1в регистре генератора на различных тактах работы появятся с учётом нулевого такта все ненулевые последовательности длиныmи каждая только один раз.

Проиллюстрируем изложенное примером 6.15

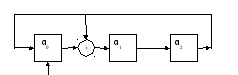
Пример 6.15.Построим генератор элементов поляGF(2³). Для этой цели используем примитивный многочлен1+x+x³. Класс вычетов{x}=α является корнем1+x+x³и примитивным элементом поляGF(2³). Схема генератора элементов поляGF(2³)и пояснение ее работы представлены на рис. 6.9.

“1

Такты	Последовательность длины 3	Многочлен	Степень α
0 1 2 3 4 5 6 7	(1 0 0) (0 1 0) (0 0 1) (1 1 0) (0 1 1) (1 1 1) (1 0 1) (1 0 0)	1 α α 2 1 + α α + α2 1 + α + α2 1 + α2 1	α 0 α 1 α 2 α 3 α 4 α 5 α6 α7 =α0

Рис 6.9 Генератор элементов поля GF(2³ )

Предварительно в ячейку α₀записывается «1». После этого осуществляются сдвиги. Выходом генератора является содержимое ячеек α_0,α₁,α₂. Работа генератора поясняется изменением содержания и представлением двоичной последовательности многочленом и степенью примитивного элемента α¹