10.3.1. Маркерный способ цикловой синхронизации на основе синхронизирующих кодовых последовательностей

В системах с необходимостью быстрого установления циклового синхронизма используются синхронизирующие кодовые последовательности. Обычно такие последовательности передаются как часть заголовка сообщения. Приемник знает эту кодовую последовательность и постоянно ищет ее в потоке данных, используя для этого корреляционный метод. Преимущество такой системы – практически мгновенное установление синфазности. Для достижения малой вероятности ложного запуска или незапуска кодовая последовательность должна быть достаточно длинной или обладать высокими автокорреляционными свойствами.

Хорошие синхронизирующие кодовые последовательности имеют малое абсолютное значение побочных максимумов корреляции. Побочный максимум корреляции – это значение корреляционной последовательности с собственной смещенной версией.

Значение побочного максимума при сдвиге на k символов N-битовой последовательности описывается функцией автокорреляции:

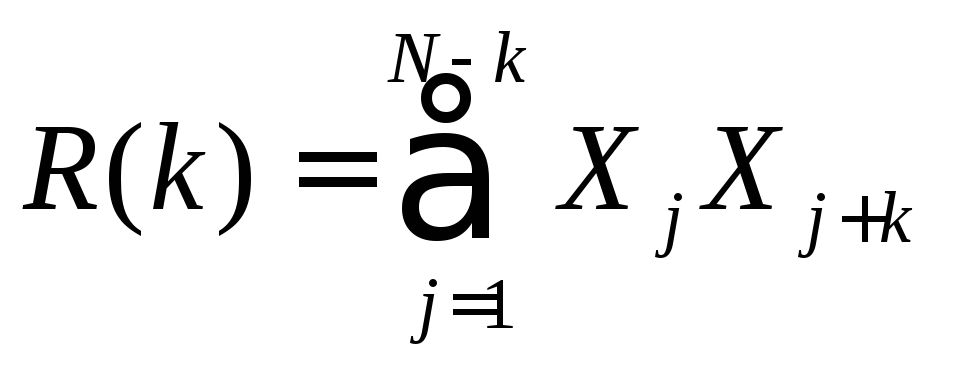
Здесь - отдельный кодовый символ, принимающий значение, а соседние символы приj>Nпредполагаются равными нулю. Желательное значение функцииR(k) представлено на рис. 10.4а.

Широко известны синхронизирующие кодовые последовательности Баркера (см. Табл. 10.1). Автокорреляционные функции последовательностей Баркера имеют побочные максимумы, не превышающие 1/Nот главного максимума, т.е.при; главный максимум

Табл. 10.1

N	Последовательность	Значения R(k) приk=N,N-1,N-2, …, 1, 0
2	+ +	+2
3	+ +-	-0 3
4	+ + + -, + + - +	-0 + 4
5	+ + + - +	+ 0 + 0 5
7	+ + + - - + -	- 0 – 0 – 0 7
11	+ + + - - - + - - + -	- 0 – 0 – 0 – 0 – 0 11
13	+ + + + + - - + + - + - +	+ 0 + 0 + 0 + 0 + 0 + 0 13

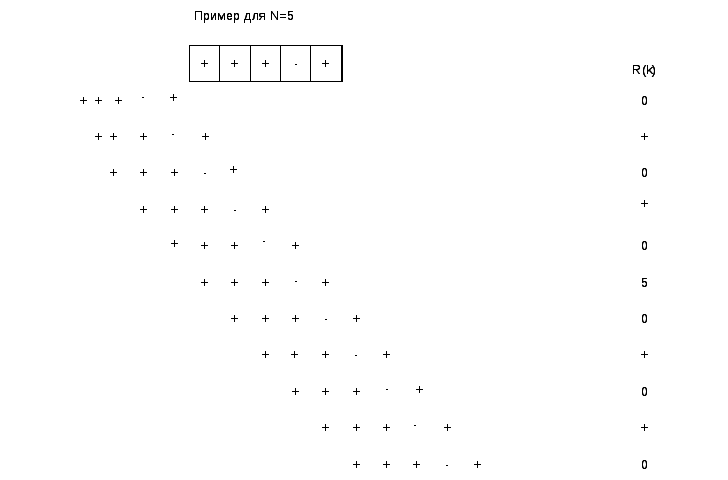
Знаки “-” и “+”обозначают -1 и +1 соответственно. Ввиду симметричности автокорреляционных функций относительно нулевого сдвига (k=0) в таблице дана только одна ее ветвь.

Свойства последовательности Баркера реализуются в предположении о нулевом значении соседних символов. К сожалению, это предположение не всегда имеет место на практике.

Уиллард нашел последовательности для случайных соседних символов, имеющих такую же длину, как и последовательности Баркера, но лучше с точки зрения минимальной вероятности ложной синхронизации. Последовательности Уилларда приведены в Табл. 10.2

Табл. 10.2

N	Последовательности
1	+
2	+ -
3	+ + -
4	+ + - -
5	+ + - + -
7	+ + + - + - -
11	+ + + - + + - + - - -
13	+ + + + + - - + - + - - -

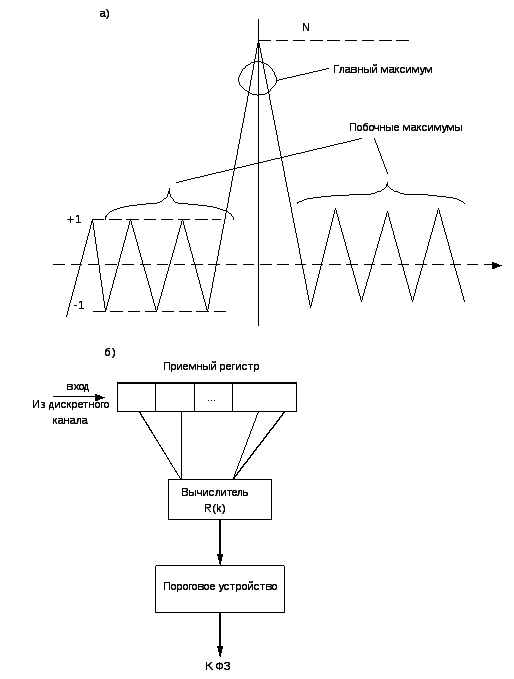
Рис. 10.4

10.4 . Способ выделения сигнала фазового запуска по зачетному отрезку

При данном способе от передатчика передается -элементная комбинация фазового запуска. В отличие от ранее рассмотренного способа на приеме в каждый момент времени анализируется толькоэлементов. Последовательность изэлементов называют зачетным отрезком, так как выделение сигнала фазового запуска производится при совпадении принятой-элементной последовательности с аналогичной последовательностью комбинации фазового запуска, содержащейся в памяти приемного устройства или получаемой в нем по заданному правилу. Моменты выделения фазового запуска должны соответствовать концу КФЗ, т.е. моменту приема элемента, поэтому всезачетных отрезков, которые могут быть получены из КФЗ, должны быть различны и однозначно связаны с их местом в КФЗ.

На рис. 10.5а показана структурная схема устройства выделения сигнала фазового запуска по зачетному отрезку. Принимаемая последовательность поступает во входной регистр и после приема очередного элемента -элементный зачетный отрезок передается в сравнивающее устройство. В этом устройстве он сравнивается со всеми отрезками КФЗ. Если не произойдет сравнения, то берется следующий зачетный отрезок, получаемый после приема очередного элемента. Если зачетный отрезок совпадает с одним из отрезков КФЗ, то в устройство определения момента выделения сигнала фазового запуска, в зависимости от вида совпавшего отрезка, в соответствующий момент выделяется сигнал фазового запуска.

При реализации способа выделения сигнала фазового запуска по зачетному отрезку наиболее часто в качестве КФЗ используется последовательность, получаемая с помощью регистров

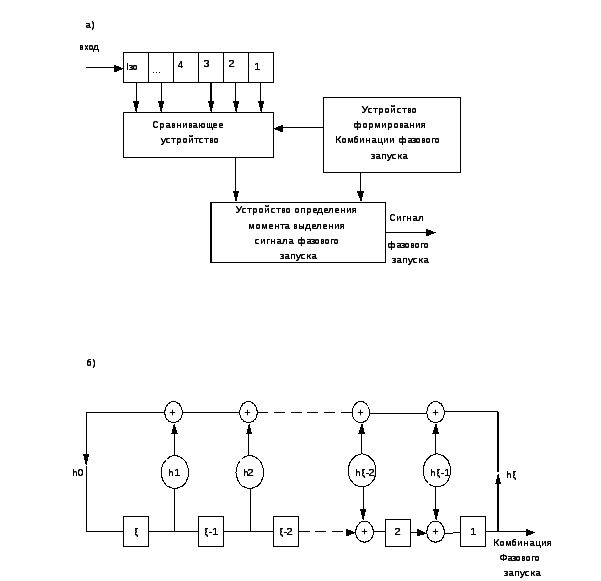
Рис. 10.5

с обратными связями. На рис. 10.5б показан такой регистр, построенный по полиному

и применяемый в качестве устройства формирования комбинации фазового запуска.

С помощью подобных регистров можно получить последовательности с периодом Т, равным показателю бинома наименьшей степени, в разложение которого входит полиномh(x). Максимальный период, равный, будет в случае, если полиномh(x) примитивный, т.е. если он не входит в разложение никакого бинома степени, меньшей. Для упрощения реализации берут полиномы веса 3. Например, можно указать следующие примитивные полиномы веса 3:

;;;;;;;.

На рис. 10.6 показана функциональная схема устройства фазирования по циклу, использующего способ выделения сигнала фазового запуска по зачетному отрезку.

В передатчике аппаратуры передачи дискретной информации имеется регистр с обратными связями, построенный по многочлену h(x) =x³+x²+1 и осуществляющий формирование комбинации фазового запуска. В приемнике АПД в составе устройства выделения сигнала фазового запуска имеется такой же регистр, но в начале процесса формирования обратная связь этого регистра разомкнута с помощью схемы. Выход регистра передатчика через открытую схему «Запрет» подключен к цепи обратной связи приемника.

Процесс фазирования начинается с записи «1» в ячейку 1 передающего регистра (табл. 10.3). Регистр приемника находится при этом в состоянии 000. На следующем такте оба регистра перейдут в одинаковое состояние 100. Начиная с этого момента на вход счетчика нулей будут подаваться нули. Это происходит потому, что последовательности, получаемые на выходах приемного и передающего регистра, совпадают. После того, как счетчикнулей отсчитает четыре нуля, на его выходах появляются сигналы, с помощью которых закрывается схема «Запрет» и открываются схемыи. Следовательно, приемный регистр начинает работать в режиме генерации последовательности, полностью совпадающей с последовательностью, генерируемой передающим регистром. Так как выход канала закрыт схемой «Запрет», то ошибки в канале не могут повлиять на последовательность, генерируемую приемным регистром. Момент фазового запуска определяется дешифратором комбинации 100. Появление этой комбинации вызывает синфазный запуск приемного распределителя по отношению к передающему.

Выбор величин иопределяется требованиями к вероятностям преждевременного запускаи незапуска.

Вероятность уменьшается с ростом, а вероятностьувеличивается. Увеличениемможно уменьшить вероятность. Окончательный выбор величиниможет быть проведен лишь при учете конкретных требований к вероятностямии структуры ошибок в дискретном канале связи.

Способ выделения сигнала фазового запуска по зачетному отрезку позволяет при простой реализации применить длинные комбинации фазового запуска. На практике широко применяется комбинация длины 512, полученная при помощи регистра, обратные связи которого соответствуют многочлену . Способ выделения сигнала фазового запуска по зачетному отрезку наиболее часто применяется в качестве составной части способа установки фазы с использованием обратного канала.

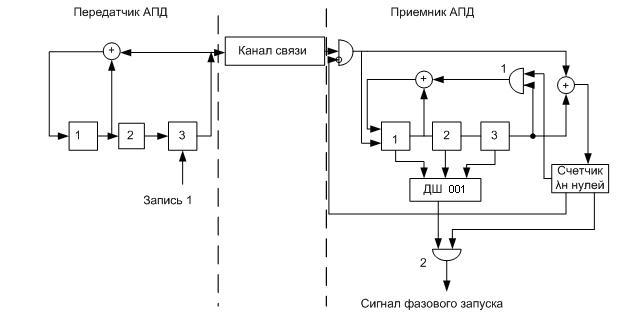
Рис. 10.6

Табл. 10.3