
- •Санкт-Петербургский государственный университет телекоммуникаций им.Проф. М.А. Бонч-Бруевича в.М. Охорзин
- •Санкт-Петербург
- •Тема 1. Основные понятия и определения в области пдс
- •1.1.Дискретность
- •Соответствующие виды сигналов:
- •1.2.Модуляция
- •1.3.Кодирование
- •1.4.Упрощенная структурная схема аппаратуры пдс.
- •Модулятор – устройство, осуществляющее модуляцию. Демодулятор осуществляет обратное преобразование. Совокупность модулятора и демодулятора образует модем.
- •1.5. Основные параметры и характеристики системы пдс
- •Тема 2. Системные характеристики систем передачи дискретных сообщений 2.1 Понятие об эталонной модели взаимодействия открытых систем
- •2.2. Понятие о телеуслугах
- •2.3 Первичные коды в системах пдс
- •2.3.1. Телеграфные коды
- •2.3.2. Коды для передачи данных
- •Тема 3. Основные характеристики уровня дискретногоканаласистем пдс
- •3.1. Понятие об искажениях дискретных сигналов
- •3.1.1. Классификация искажений
- •3.1.2.Характеристические краевые искажения
- •3.1.3 Краевые искажения типа преобладаний
- •3.1.4.Случайные искажения
- •3.2.Понятие о методах регистрации дискретных сигналов
- •3.2.1.Метод стробирования
- •3.2.2. Интегральный метод
- •Интегрирование в промежутке, меньшем длительности элементарной посылки
- •3.3 Оценка эффективности методов регистрации
- •3.3.1.Распределение краевых искажений
- •3.3.2. Распределение дроблений
- •3.3.3. Расчет вероятности ошибки при краевых искажениях
- •3.3.4.Расчет вероятности ошибки при дроблениях
- •3.4.Модели дискретных каналов
- •3.4.1.Поток ошибок в дискретном канале
- •3.4.2.Методы выявления и исследования последовательностей ошибок
- •3.4.3 Основные закономерности распределения ошибок в реальных каналах связи
- •3.4.4 Математические модели дискретных каналов с группированием ошибок
- •А. Модель неоднородного канала.
- •Б. Двухпараметрическая модель дискретного канала
- •Тема 4. Устройство синхронизации по элементам (усп).
- •4.1.Назначение и классификация
- •Основные элементы устройства , реализующего фапч:
- •4.2. Необходимость поэлементной синхронизации . Расчет времени удержания синхронизма.
- •4.3.Схема фапч с дискретным управлением.
- •4.4.Основные характеристики системы фапч.
- •Тема 5. Линейные (n,k)-коды
- •5.1. Определение помехоустойчивых кодов и их общие характеристики
- •5.1.1. Принципы построения помехоустойчивых кодов
- •5.1.2. Основные характеристики помехоустойчивых кодов
- •5.1.3 Классификация помехоустойчивых кодов
- •5.1.4.Граничные соотношения между характеристиками помехоустойчивых кодов
- •5.1.5.Задачи
- •5.2. Групповые коды и способы их описания
- •5.2.1. Основные алгебраические системы, используемые в теории кодирования
- •5.2.2. Способы представления кодовых комбинаций
- •5.2.3. Определение группового кода
- •5.2.4. Матричное описание групповых кодов
- •5.2.5. Задачи
- •5.3. Другие свойства групповых кодов
- •5.3.1. Корректирующие свойства групповых кодов
- •5.3.2. Процедуры кодирования и декодирования для группового кода
- •5.3.3. Укорочение кода
- •5.3.4. Оценка эффективности групповых кодов
- •5.3.5. Смежно-групповые коды
- •5.3.6. Задачи
- •5.4. Примеры групповых кодов
- •5.4.1. Коды с единственной проверкой на четность
- •5.4.2. Коды Хэмминга
- •5.4.3. Итеративные коды.
- •5.4.4 Задачи
- •Тема 6. Двоичные циклические (n,k) - коды
- •6.1. Основные алгебраические системы, используемые в теории кодирования.
- •6.2. Определение циклического кода
- •6.3. Построение порождающей и проверочной матриц циклических кодов.
- •6.4. Коды Боуза-Чоудхури-Хоквингема (бчх).
- •6.5. Выбор порождающего многочлена для кода бчх
- •6.6. Эффективность двоичных кодов бчх
- •6.6.1. Задачи
- •6.7. Кодирующие и декодирующие устройства циклических кодов
- •6.7.1 Процедура кодирования и декодирования для циклических кодов
- •6.7.2. Линейные переключательные схемы, используемые в кодирующих и декодирующих устройствах циклических кодов
- •6.7.3. Схемы кодирующих устройств циклических кодов
- •6.7.4. Декодирующие устройства циклических кодов
- •6.7.5. Задачи
- •Тема 7. Коды Рида- Соломона (рс)
- •7.1. Определение и основные свойства
- •Пример 7.1
- •Пример 7.2
- •7.1.1. Расширенные рс-коды
- •Пример 7.3
- •7.1.2. Укороченные рс-коды
- •7.1.3. Отображение рс-кодов над gf(2m) на двоичные коды
- •7.1.4. Способы кодирования и декодирования рс-кодов
- •1. Многочлен локаторов ошибок:
- •2.Синдромный многочлен
- •3. Многочлен значений ошибок
- •7.2. Быстрое декодирование кодов бчх
- •7.2.1. Ключевое уравнение
- •7.2.2. Решение ключевого уравнения
- •7.2.3. Примеры решения ключевого уравнения
- •7.3.Кодирование на основе решения ключевого уравнения
- •7.4.Задачи
- •Тема 8. Непрерывные коды
- •8.1. Сверточное кодирование
- •8.2. Представление сверточного кодера
- •8.2.1. Представление связи
- •8.2.1.1. Реакция кодера на импульсное возмущение
- •8.2.1.2. Полиномиальное представление
- •8.2.2. Представление состояния и диаграмма состояний
- •8.2.3. Древовидные диаграммы
- •8.2.4. Решетчатая диаграмма
- •8.3. Формулировка задачи сверточного декодирования
- •8.3.1. Алгоритм сверточного декодирования Витерби
- •8.3.2. Пример сверточного декодирования Витерби
- •8.4. Декодирование с мягким решением
- •8.4.1. Модель канала с абгш
- •2.1.2. Передача двоичных сигналов по каналам с абгш
- •2.1.3. Алгоритм Витерби с Евклидовой метрикой
- •8.5. Связь с блоковыми кодами
- •8.5.1. Терминированная конструкция (нулевой хвост)
- •8.5.2. Усеченная конструкция (direct truncation)
- •8.5.3. Кольцевая (циклическая или циклически замкнутая) (tail-biting) конструкция
- •8.5.4. Распределение весов
- •8.6. Модифицированный граф состояний
- •8.7. Решение задач
- •8.7.1. Задачи
- •8.7.2. Решение
- •8.3.2.1. Процедура сложения, сравнения и выбора
- •8.3.2.2. Вид процедуры сложения, сравнения и выбора на решетке
- •8.3.3. Память путей и синхронизация
- •8.4. Свойства сверточных кодов
- •8.4.1. Пространственные характеристики сверточных кодов
- •8.4.1.1. Возможности сверточного кода в коррекции ошибок
- •8.4.2. Систематические и несистематические сверточные коды
- •8.4.3. Распространение катастрофических ошибок в сверточных кодах
- •8.4.4. Границы рабочих характеристик сверточных кодов
- •8.4.5. Эффективность кодирования
- •8.4.6. Наиболее известные сверточные коды
- •8.5. Задачи
- •Тема 9. Некоторые специальные классы кодов. Составные коды
- •9.1. Коды для исправления пачек ошибок
- •9.2. Коды на основе последовательностей максимальной длины
- •9.3. Коды для асимметричных каналов
- •9.3.1. Коды с постоянным весом
- •9.3.2. Коды Бергера
- •9.4 Каскадные коды
- •9.4.1. Принципы построения каскадных кодов
- •9.4.2. Режимы использования каскадных кодов
- •9.4.3. Построение двоичных каскадных кодов на основе кодов Рида–Соломона и Боуза–Чоудхури–Хоквингема
- •Пример 9.2.
- •Пример 9.3.
- •9.5. Задачи
- •Тема 10. Цикловая синхронизация
- •10.1 Назначение и классификация способов цикловой синхронизации
- •10.2. Способ установки фазы приемного распределителя путем сдвига.
- •10.3. Способ мгновенной установки фазы
- •10.3.1. Маркерный способ цикловой синхронизации на основе синхронизирующих кодовых последовательностей
- •10.4 . Способ выделения сигнала фазового запуска по зачетному отрезку
- •Тема 11. Системные методы защиты от ошибок без обратной связи
- •11.1. Классификация и основные характеристики систем повышения достоверности
- •11.1.1. Теоретические основы системных методов защиты от ошибок
- •11.1.2. Классификация системных методов защиты от ошибок
- •11.1.3 .Основные параметры и характеристики систем повышения достоверности
- •11.2. Методы повышения достоверности в однонаправленных системах
- •11.2.1.Однонаправленные системы с многократным повторением сообщений
- •11.2.2.Однонаправленные системы с исправляющим ошибки кодом
- •11.2.3.Однонаправленные системы с исправлением стираний
- •11.3. Задачи
- •Тема 12. Системные методы защиты от ошибок с обратной связью
- •12.1. Системы повышения достоверности с решающей обратной связью с непрерывной последовательной передачей сообщений и блокировкой (рос-пПбл).Общие положения
- •12.2. Описание работы системы рос-пПбл
- •12.3. Режим переспроса
- •12.4. Расчет параметров системы рос-пПбл Относительная скорость передачи
- •Расчет вероятности ошибок на выходе системы
- •12.5. Рекомендации по выбору оптимального кода
- •Охарактеризуем поток ошибок, пропущенных в приемник сообщений средней вероятностью ошибки на бит, равной и показателем группирования ошибок.
- •12.6. Выбор порождающего многочлена
- •12.7. Задачи
- •Приложение 1. Коды бчх
- •Приложение 4
- •Список использованных источников
- •Предметный указатель
- •Тема 1. Основные понятия и определения в области пдс………………..……....2
- •Тема 2. Системные характеристики систем передачи дискретных сообще……...11
- •Тема 3. Основные характеристики уровня дискретного канала пдс…………………21
- •Тема 4. Устройство синхронизации по элементам (усп)…………………………...50
- •Тема 5. Линейные (n,k)-коды…….………………………………………………………..54
- •Тема 6. Двоичные циклические (n,k) – коды…………………………………… …….105
- •Тема 7. Коды Рида- Соломона (рс)…………………………………………..………..165
- •7.1.3. Отображение рс-кодов над gf(2m) на двоичные коды…………………….170
- •Тема 8. Непрерывные коды……………………………………………..………………..185
- •Тема 9. Некоторые специальные классы кодов. Составные коды………………..……210
- •9.4.1. Принципы построения каскадных кодов…………………………………………………215
- •9.4.2. Режимы использования каскадных кодов……………………………………………….218
- •9.4.3. Построение двоичных каскадных кодов на основе кодов Рида–Соломона и Боуза–Чоудхури–Хоквингема………………..……………………………………………….…219
- •Тема 11. Системные методы защиты от ошибок без обратной связи………………..……234
- •Тема 12. Системные методы защиты от ошибок с обратной связью…..…………….244
8.5. Связь с блоковыми кодами
Из приведенного выше описания сверточных кодеров видно, что существует связь между сверточными и блоковыми кодами. Как уже отмечалось ранее, информационные последовательности обычно разбивают на блоки конечной длины (например, несколько тысяч бит). Как правило, в конце каждого информационного блока добавляется фиксированная последовательность длины т. Эта последовательность представляет собой уникальное слово, которое служит для синхронизации приемника и заставляет сверточный кодер возвращаться к известному (начальному) состоянию.
В
дальнейшем, ради простоты изложения,
будем считать, что С несистематический
(FIR)
сверточный код со свободным расстоянием
![]() ,
образованный сверточным кодером памяти
m
и скорости 1/n.
Аналогичные характеристики относятся
и к RSC
кодам.
,
образованный сверточным кодером памяти
m
и скорости 1/n.
Аналогичные характеристики относятся
и к RSC
кодам.
8.5.1. Терминированная конструкция (нулевой хвост)
Добавление
«хвоста» из т нулей к каждому информационному
блоку длины (К—m)
приводит к завершению всех путей на
треллисе, соответствующих
![]() кодовым
словам, в нулевом состоянии. В результате
получаем линейный блоковый (nK,(K-m),dZT)
код
CZT.
Если
К
достаточно велико, то скорость кода
CZT
приближается к скорости кода С. Если
К>т
и
К достаточно
велико, то минимальное расстояние кода
CZT
удовлетворяет
равенству
dZT=
кодовым
словам, в нулевом состоянии. В результате
получаем линейный блоковый (nK,(K-m),dZT)
код
CZT.
Если
К
достаточно велико, то скорость кода
CZT
приближается к скорости кода С. Если
К>т
и
К достаточно
велико, то минимальное расстояние кода
CZT
удовлетворяет
равенству
dZT=
![]() .
.
Пример 2. Пусть С сверточный код со свободным расстоянием = 5 , порождаемый кодером памяти 2 и скорости 1/2 . Предположим, что кодируется информационный вектор К =3 бит, дополненный т = 2 нулями. Тогда терминированная конструкция приводит к двоичному блоковому линейному (10, 3, 5) коду CZT с порождающей матрицей

Распределение весов этого кода равно А(х) = 1 + Зх5 + Зx6 + и = 5. Скорость кода CZT равна 3/10, т.е. меньше скорости k/n = 1/2 исходного кода С.
8.5.2. Усеченная конструкция (direct truncation)
В
этом случае кодовые слова линейного
блокового (nК,
К, dDT)
кода ассоциируются с кодовыми
последовательностями свер¬точного
кодера скорости k/n,
которые соответствуют на треллисе всем
путям, начинающимся в нулевом состоянии
и закан¬чивающимся, после ввода К
информационных бит, в произ¬вольном
состоянии. Минимальное расстояние
полученного блокового кода удовлетворяет
неравенству dDT
< ![]() .
.
8.5.3. Кольцевая (циклическая или циклически замкнутая) (tail-biting) конструкция
Кодовые слова кольцевой конструкции блокового кода представляют собой множество всех путей на решетке, которые начинаются и
заканчиваются
в
одном и том же состоянии
кодовой решетки. Скорость полученного
блокового
(пК, К, dTB)
кода совпадает со скоростью 1/п
исходного сверточного кода. Однако даже
при достаточно большом К > т минимальное
расстояние удовлетворяет условию dTB
![]()
![]()
Пример 3. Рассмотрим кодер скорости 1/2 памяти 2 на Рисунке 29. Предположим, что кодируется блок К= 5 информационных символов. Тогда кольцевая конструкция приводит к двоичному линейному блоковому (10, 5, dTB) коду с порождающей матрицей

8.5.4. Распределение весов
В этом разделе рассматривается метод определения спектра весов линейного блокового кода, построенного из сверточного кода скорости 1/n с помощью рассмотренных выше конструкций [WV], Обозначим Ω(x) переходную матрицу состояний кодера размера 2т х 2т и вида:
![]() (x)
=
(x)
= ![]() (2.1)
(2.1)
где
![]() =1,
если и только если имеется переход из
состояния
i
в
состояние
j.
В противном случае
=1,
если и только если имеется переход из
состояния
i
в
состояние
j.
В противном случае
![]() =
0. Величина
=
0. Величина
![]() равна
Хеммингову весу соответствующего
выходного вектора (длины
п).
равна
Хеммингову весу соответствующего
выходного вектора (длины
п).
Пример 4. Для сверточного кодера переходная матрица состояний Ω(x) равна
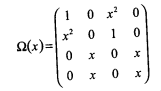
Распределение
весов двоичного линейного блокового
(n,
к)
кода, построенного любым из рассмотренных
выше способов, может быть получено
просто возведением данной переходной
матрицы в l-ую
степень, обозначенную ![]() и комбинированием различных членов.
и комбинированием различных членов.
Каждый
элемент ![]() переходной матрицы дает распределение
весов путей на решетке, которые начинаются
в состоянии
i
и заканчиваются в состоянии
j
через l
шагов (тактов ввода). Для конструкции
ZT
(нулевой хвост) значение =
к + т, тогда
как для конструкций DT
и ТВ l
=
k.
Распределение весов для каждой из
рассмотренных выше конструкций было
получено следующим способом.
переходной матрицы дает распределение
весов путей на решетке, которые начинаются
в состоянии
i
и заканчиваются в состоянии
j
через l
шагов (тактов ввода). Для конструкции
ZT
(нулевой хвост) значение =
к + т, тогда
как для конструкций DT
и ТВ l
=
k.
Распределение весов для каждой из
рассмотренных выше конструкций было
получено следующим способом.
Терминированная конструкция (ZT):
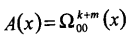 (2.2)
(2.2)
Усеченная конструкция (DT):
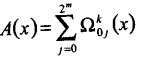 (2.3)
(2.3)
Кольцевая конструкция (ТВ):
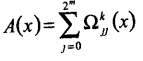 (2.4)
(2.4)
Пример 5. Рассмотрим снова сверточный кодер памяти 2 и скорости 1/2. Для него находим:
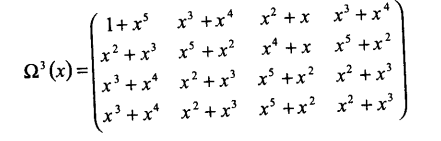
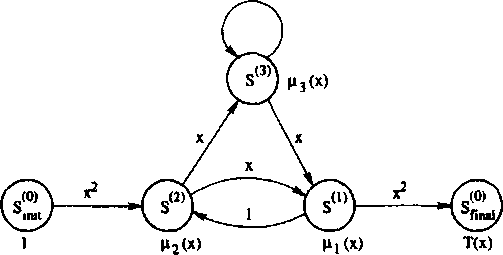
Рис. 2.1. Модифицированная диаграмма состояний кодера памяти 2 и скорости ½.
Распределение весов усеченной конструкции из Примера 4 получается суммированием членов первой строки полученной выше матрицы.[3].
