7.2.2. Решение ключевого уравнения

а). Алгоритм Питерсона.

У. Питерсон [1] представил ключевое уравнение в матричной форме:

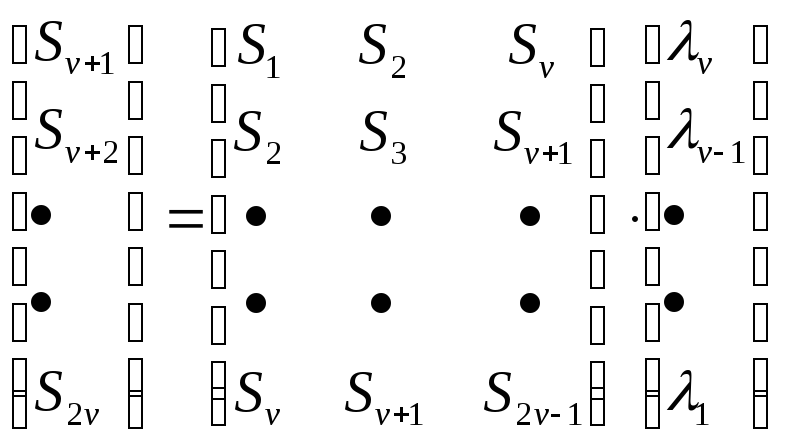
Таким образом, задача определения коэффициентов многочлена локаторов ошибок сводится к прямому решению системы v линейных уравнений с v неизвестными.

б) Алгоритм Евклида.

Известно, что, если существует наибольший общий делитель d(x) двух многочленов а(х) и b(х), то существуют многочлены f(x) и g(x) такие, что справедливо: a(x)f{x)+b(x)g(x)=d(x).

Многочлен d(x) может быть найден по алгоритму Евклида, который состоит в последовательном делении с остатком а(х) на b(х), затем b(х) на первый остаток r₁(х), затем r₁(х) на второй остаток r₂(х) и т.д.

При декодировании кодов БЧХ интересуются не конечным результатом алгоритма Евклида, а промежуточными результатами, которые можно представить в виде: a(x)f(x)+b(x)g(x)=r(x).

У. Сугияма и его соавторы [3] использовали этот результат для решения ключевого уравнения следующим образом: b(x)g(x)= r_i(x) (mod a(x)), полагая,

а(х)=х^2t, b(x)=S(x), g_l(x)=Λ_i(x), r_i(x)=Ω_i(x).

При этом используется свойство алгоритма Евклида:

deg[g_i(x)]+deg[r_i-l(x)]=deg[a(x)].

Если а(х)=х^2t, то deg[Λ_i(x)]+deg[Ω_i-_l(x))=2t,

deg[Λ_i(x)]+deg[Ω_i(x))<2t.

При появлении v≤t ошибок имеем: deg[Ω(x)]< deg[Λ (x)] ≤t.

Существует единственный с точностью до постоянного множителя (элемента поля) многочлен Λ(х) степени ≤ t, удовлетворяющий уравнению:

Ω_i(x) =S(x) Λ_i(x) (mod x^2t),

если deg[Ω_i-1(x)]≥ t при deg[Λ_i(x)]≤ t

и deg[Ω_i(x)]< t при deg[Λ_i+1,(x)] > t.

Поэтому промежуточные результаты на I-ом шаге дают единственное интересующее нас решение ключевого уравнения.

Таким образом, для решения ключевого уравнения следует применять алгоритм Евклида до тех пор, пока не будет выполнено условие

deg[Ω_i(x)]< t.

Итак, алгоритм Евклида решения ключевого уравнения по методу У. Сугиямы и др. сводится к следующему:

1. Применить алгоритм Евклида к а(х)=х^2t и b(x)=S(x).

2. Использовать начальные условия:

Λ_-1(х)=0,

Λ₀(х)=1,

Ω_-1(x)=x^2t,

Ω₀(x)=S(x).

3. Остановиться, если deg[Ω_i(x)]< t.

4. Положить Λ(х)= Λ_i(x) и Ω(x)= Ω_i(x).

При вычислении значений Λ_i(x) и Ω_i(x) следует использовать свойство алгоритма Евклида: каждое из значений Λ_i(x) и Ω_i(x) получается из двух предшествующих значений по следующей общей формуле:

E_i(x)=E_i-2(x)+q_i(х)E_i-1(x) , где .

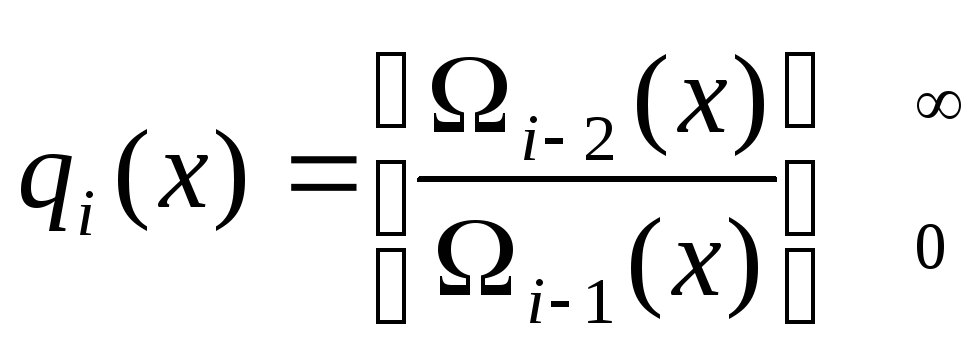В квадратных скобках записано частное от деления указанных многочленов т,е. многочлен степени 0 и более.

в) Алгоритм Берлекемпа-Месси.

На рис.7.1 представлен доработанный алгоритм, позволяющий кроме А(х) получать также и многочлен значений ошибок и Ω(x).

Этот алгоритм был предложен Э. Берлекемпом и Дж. Месси[4] как итеративный процесс построения минимального линейного регистра сдвига с обратной связью, аналогичного схеме решения разностных уравнений, генерирующего все компоненты синдромного многочлена S(x) no υ первым.

Целью алгоритма является нахождение коэффициентов многочлена локаторов ошибок Λ(х)_, значение которых определяет вид обратных связей регистра.

г) Алгоритм Форни

Д. Форни (см. раздел 7.1) получил выражение для вычисления значения ошибки, если известны многочлены значения ошибок Ω(x) и локаторов ошибок:

,

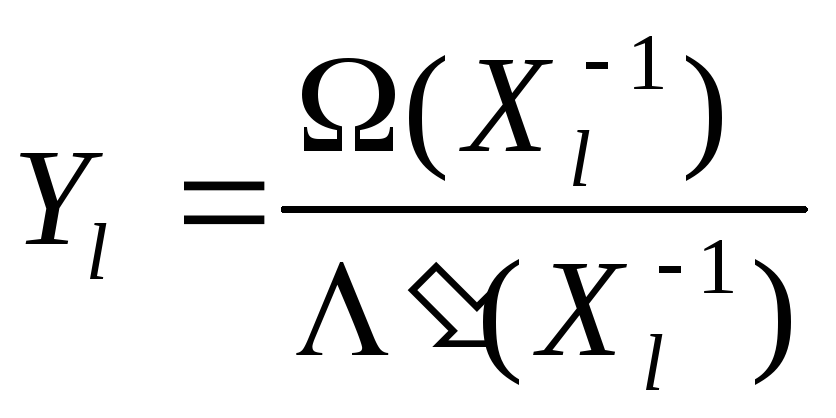где Х_l^-1- корень многочлена Λ(х), обратный локатору ошибки Х_l, Λ^′(Х ) –производная от много члена Λ(х).