
- •Санкт-Петербургский государственный университет телекоммуникаций им.Проф. М.А. Бонч-Бруевича в.М. Охорзин
- •Санкт-Петербург
- •Тема 1. Основные понятия и определения в области пдс
- •1.1.Дискретность
- •Соответствующие виды сигналов:
- •1.2.Модуляция
- •1.3.Кодирование
- •1.4.Упрощенная структурная схема аппаратуры пдс.
- •Модулятор – устройство, осуществляющее модуляцию. Демодулятор осуществляет обратное преобразование. Совокупность модулятора и демодулятора образует модем.
- •1.5. Основные параметры и характеристики системы пдс
- •Тема 2. Системные характеристики систем передачи дискретных сообщений 2.1 Понятие об эталонной модели взаимодействия открытых систем
- •2.2. Понятие о телеуслугах
- •2.3 Первичные коды в системах пдс
- •2.3.1. Телеграфные коды
- •2.3.2. Коды для передачи данных
- •Тема 3. Основные характеристики уровня дискретногоканаласистем пдс
- •3.1. Понятие об искажениях дискретных сигналов
- •3.1.1. Классификация искажений
- •3.1.2.Характеристические краевые искажения
- •3.1.3 Краевые искажения типа преобладаний
- •3.1.4.Случайные искажения
- •3.2.Понятие о методах регистрации дискретных сигналов
- •3.2.1.Метод стробирования
- •3.2.2. Интегральный метод
- •Интегрирование в промежутке, меньшем длительности элементарной посылки
- •3.3 Оценка эффективности методов регистрации
- •3.3.1.Распределение краевых искажений
- •3.3.2. Распределение дроблений
- •3.3.3. Расчет вероятности ошибки при краевых искажениях
- •3.3.4.Расчет вероятности ошибки при дроблениях
- •3.4.Модели дискретных каналов
- •3.4.1.Поток ошибок в дискретном канале
- •3.4.2.Методы выявления и исследования последовательностей ошибок
- •3.4.3 Основные закономерности распределения ошибок в реальных каналах связи
- •3.4.4 Математические модели дискретных каналов с группированием ошибок
- •А. Модель неоднородного канала.
- •Б. Двухпараметрическая модель дискретного канала
- •Тема 4. Устройство синхронизации по элементам (усп).
- •4.1.Назначение и классификация
- •Основные элементы устройства , реализующего фапч:
- •4.2. Необходимость поэлементной синхронизации . Расчет времени удержания синхронизма.
- •4.3.Схема фапч с дискретным управлением.
- •4.4.Основные характеристики системы фапч.
- •Тема 5. Линейные (n,k)-коды
- •5.1. Определение помехоустойчивых кодов и их общие характеристики
- •5.1.1. Принципы построения помехоустойчивых кодов
- •5.1.2. Основные характеристики помехоустойчивых кодов
- •5.1.3 Классификация помехоустойчивых кодов
- •5.1.4.Граничные соотношения между характеристиками помехоустойчивых кодов
- •5.1.5.Задачи
- •5.2. Групповые коды и способы их описания
- •5.2.1. Основные алгебраические системы, используемые в теории кодирования
- •5.2.2. Способы представления кодовых комбинаций
- •5.2.3. Определение группового кода
- •5.2.4. Матричное описание групповых кодов
- •5.2.5. Задачи
- •5.3. Другие свойства групповых кодов
- •5.3.1. Корректирующие свойства групповых кодов
- •5.3.2. Процедуры кодирования и декодирования для группового кода
- •5.3.3. Укорочение кода
- •5.3.4. Оценка эффективности групповых кодов
- •5.3.5. Смежно-групповые коды
- •5.3.6. Задачи
- •5.4. Примеры групповых кодов
- •5.4.1. Коды с единственной проверкой на четность
- •5.4.2. Коды Хэмминга
- •5.4.3. Итеративные коды.
- •5.4.4 Задачи
- •Тема 6. Двоичные циклические (n,k) - коды
- •6.1. Основные алгебраические системы, используемые в теории кодирования.
- •6.2. Определение циклического кода
- •6.3. Построение порождающей и проверочной матриц циклических кодов.
- •6.4. Коды Боуза-Чоудхури-Хоквингема (бчх).
- •6.5. Выбор порождающего многочлена для кода бчх
- •6.6. Эффективность двоичных кодов бчх
- •6.6.1. Задачи
- •6.7. Кодирующие и декодирующие устройства циклических кодов
- •6.7.1 Процедура кодирования и декодирования для циклических кодов
- •6.7.2. Линейные переключательные схемы, используемые в кодирующих и декодирующих устройствах циклических кодов
- •6.7.3. Схемы кодирующих устройств циклических кодов
- •6.7.4. Декодирующие устройства циклических кодов
- •6.7.5. Задачи
- •Тема 7. Коды Рида- Соломона (рс)
- •7.1. Определение и основные свойства
- •Пример 7.1
- •Пример 7.2
- •7.1.1. Расширенные рс-коды
- •Пример 7.3
- •7.1.2. Укороченные рс-коды
- •7.1.3. Отображение рс-кодов над gf(2m) на двоичные коды
- •7.1.4. Способы кодирования и декодирования рс-кодов
- •1. Многочлен локаторов ошибок:
- •2.Синдромный многочлен
- •3. Многочлен значений ошибок
- •7.2. Быстрое декодирование кодов бчх
- •7.2.1. Ключевое уравнение
- •7.2.2. Решение ключевого уравнения
- •7.2.3. Примеры решения ключевого уравнения
- •7.3.Кодирование на основе решения ключевого уравнения
- •7.4.Задачи
- •Тема 8. Непрерывные коды
- •8.1. Сверточное кодирование
- •8.2. Представление сверточного кодера
- •8.2.1. Представление связи
- •8.2.1.1. Реакция кодера на импульсное возмущение
- •8.2.1.2. Полиномиальное представление
- •8.2.2. Представление состояния и диаграмма состояний
- •8.2.3. Древовидные диаграммы
- •8.2.4. Решетчатая диаграмма
- •8.3. Формулировка задачи сверточного декодирования
- •8.3.1. Алгоритм сверточного декодирования Витерби
- •8.3.2. Пример сверточного декодирования Витерби
- •8.4. Декодирование с мягким решением
- •8.4.1. Модель канала с абгш
- •2.1.2. Передача двоичных сигналов по каналам с абгш
- •2.1.3. Алгоритм Витерби с Евклидовой метрикой
- •8.5. Связь с блоковыми кодами
- •8.5.1. Терминированная конструкция (нулевой хвост)
- •8.5.2. Усеченная конструкция (direct truncation)
- •8.5.3. Кольцевая (циклическая или циклически замкнутая) (tail-biting) конструкция
- •8.5.4. Распределение весов
- •8.6. Модифицированный граф состояний
- •8.7. Решение задач
- •8.7.1. Задачи
- •8.7.2. Решение
- •8.3.2.1. Процедура сложения, сравнения и выбора
- •8.3.2.2. Вид процедуры сложения, сравнения и выбора на решетке
- •8.3.3. Память путей и синхронизация
- •8.4. Свойства сверточных кодов
- •8.4.1. Пространственные характеристики сверточных кодов
- •8.4.1.1. Возможности сверточного кода в коррекции ошибок
- •8.4.2. Систематические и несистематические сверточные коды
- •8.4.3. Распространение катастрофических ошибок в сверточных кодах
- •8.4.4. Границы рабочих характеристик сверточных кодов
- •8.4.5. Эффективность кодирования
- •8.4.6. Наиболее известные сверточные коды
- •8.5. Задачи
- •Тема 9. Некоторые специальные классы кодов. Составные коды
- •9.1. Коды для исправления пачек ошибок
- •9.2. Коды на основе последовательностей максимальной длины
- •9.3. Коды для асимметричных каналов
- •9.3.1. Коды с постоянным весом
- •9.3.2. Коды Бергера
- •9.4 Каскадные коды
- •9.4.1. Принципы построения каскадных кодов
- •9.4.2. Режимы использования каскадных кодов
- •9.4.3. Построение двоичных каскадных кодов на основе кодов Рида–Соломона и Боуза–Чоудхури–Хоквингема
- •Пример 9.2.
- •Пример 9.3.
- •9.5. Задачи
- •Тема 10. Цикловая синхронизация
- •10.1 Назначение и классификация способов цикловой синхронизации
- •10.2. Способ установки фазы приемного распределителя путем сдвига.
- •10.3. Способ мгновенной установки фазы
- •10.3.1. Маркерный способ цикловой синхронизации на основе синхронизирующих кодовых последовательностей
- •10.4 . Способ выделения сигнала фазового запуска по зачетному отрезку
- •Тема 11. Системные методы защиты от ошибок без обратной связи
- •11.1. Классификация и основные характеристики систем повышения достоверности
- •11.1.1. Теоретические основы системных методов защиты от ошибок
- •11.1.2. Классификация системных методов защиты от ошибок
- •11.1.3 .Основные параметры и характеристики систем повышения достоверности
- •11.2. Методы повышения достоверности в однонаправленных системах
- •11.2.1.Однонаправленные системы с многократным повторением сообщений
- •11.2.2.Однонаправленные системы с исправляющим ошибки кодом
- •11.2.3.Однонаправленные системы с исправлением стираний
- •11.3. Задачи
- •Тема 12. Системные методы защиты от ошибок с обратной связью
- •12.1. Системы повышения достоверности с решающей обратной связью с непрерывной последовательной передачей сообщений и блокировкой (рос-пПбл).Общие положения
- •12.2. Описание работы системы рос-пПбл
- •12.3. Режим переспроса
- •12.4. Расчет параметров системы рос-пПбл Относительная скорость передачи
- •Расчет вероятности ошибок на выходе системы
- •12.5. Рекомендации по выбору оптимального кода
- •Охарактеризуем поток ошибок, пропущенных в приемник сообщений средней вероятностью ошибки на бит, равной и показателем группирования ошибок.
- •12.6. Выбор порождающего многочлена
- •12.7. Задачи
- •Приложение 1. Коды бчх
- •Приложение 4
- •Список использованных источников
- •Предметный указатель
- •Тема 1. Основные понятия и определения в области пдс………………..……....2
- •Тема 2. Системные характеристики систем передачи дискретных сообще……...11
- •Тема 3. Основные характеристики уровня дискретного канала пдс…………………21
- •Тема 4. Устройство синхронизации по элементам (усп)…………………………...50
- •Тема 5. Линейные (n,k)-коды…….………………………………………………………..54
- •Тема 6. Двоичные циклические (n,k) – коды…………………………………… …….105
- •Тема 7. Коды Рида- Соломона (рс)…………………………………………..………..165
- •7.1.3. Отображение рс-кодов над gf(2m) на двоичные коды…………………….170
- •Тема 8. Непрерывные коды……………………………………………..………………..185
- •Тема 9. Некоторые специальные классы кодов. Составные коды………………..……210
- •9.4.1. Принципы построения каскадных кодов…………………………………………………215
- •9.4.2. Режимы использования каскадных кодов……………………………………………….218
- •9.4.3. Построение двоичных каскадных кодов на основе кодов Рида–Соломона и Боуза–Чоудхури–Хоквингема………………..……………………………………………….…219
- •Тема 11. Системные методы защиты от ошибок без обратной связи………………..……234
- •Тема 12. Системные методы защиты от ошибок с обратной связью…..…………….244
5.4.2. Коды Хэмминга
Кодом Хэмминга
называется (n, k)
– код, который задается матрицей проверокH(n,k),
имеющей![]() строк и
строк и![]() столбцов, причем столбцамиH(n,k)являются все различные ненулевые
двоичные последовательности длиныm(m– разрядные двоичные
числа от 1 до
столбцов, причем столбцамиH(n,k)являются все различные ненулевые
двоичные последовательности длиныm(m– разрядные двоичные
числа от 1 до![]() ).
).
Длина кодовой
комбинации кода Хэмминга равна
![]() .
.
Число информационных
элементов определяется как
![]() .
.
Итак, код Хэмминга полностью задается числом m– количеством проверочных элементов в кодовой комбинации.
Зная вид матрицы H(n,k), можно определить корректирующие свойства (n, k) – кода Хэмминга. Так как все столбцы матрицы проверок различны, то никакие два столбцаH(n,k)не являются линейно зависимыми. Наряду с этим, для любого числаmвсегда можно указать три столбца матрицыH(n,k), которые линейно зависимы, например, столбцы, соответствующие числам 1, 2, 3. Следовательно, для любого (n, k) – кода Хэммингаdmin=3.
Код Хэмминга является одним из немногочисленных примеров совершенного кода.
Действительно,
поскольку (n, k)
– код Хэмминга исправляет все одиночные
ошибки, то все образцы одиночных ошибок
(а их всего насчитывается![]() вариантов) должны разместиться в
различных смежных классах, число которых
также равно
вариантов) должны разместиться в
различных смежных классах, число которых
также равно![]() .
Следовательно, помимо смежных классов,
содержащих образцы одиночных ошибок,
никаких других в таблице декодирования
не имеется, что и подтверждает совершенность
кода Хэмминга.
.
Следовательно, помимо смежных классов,
содержащих образцы одиночных ошибок,
никаких других в таблице декодирования
не имеется, что и подтверждает совершенность
кода Хэмминга.
При фиксированном
числе
![]() можно построить код Хэмминга любой
длины (
можно построить код Хэмминга любой
длины (![]() )
путем укорочения (n,
k) – кода. Укорочение
не уменьшает минимальное кодовое
расстояние. В силу того, что для любого
числаn существует
код Хэмминга,любой групповой код с
исправлением одиночных ошибок принято
называть кодом Хэмминга.
)
путем укорочения (n,
k) – кода. Укорочение
не уменьшает минимальное кодовое
расстояние. В силу того, что для любого
числаn существует
код Хэмминга,любой групповой код с
исправлением одиночных ошибок принято
называть кодом Хэмминга.
Пример 5.13.Определим параметры кодов Хэмминга естественной длины для различных значений m. Результаты представим в виде таблицы.
-
m

k

1
1
0
0
2
3
1
0,33
3
7
4
0,57
4
15
11
0,74
5
31
26
0,84
6
63
57
0,91
7
127
120
0,95
и т.д.
Очевидно, что
минимальная длина кода Хэмминга, имеющего
практическое значение, есть 3. При
увеличении nотношение![]() возрастает и стремится к 1.
возрастает и стремится к 1.
Пример 5.14. Рассмотрим код Хэмминга (7,4). Матрица проверок этого кода состоит из 7 трехразрядных двоичных чисел от 1 до 7:
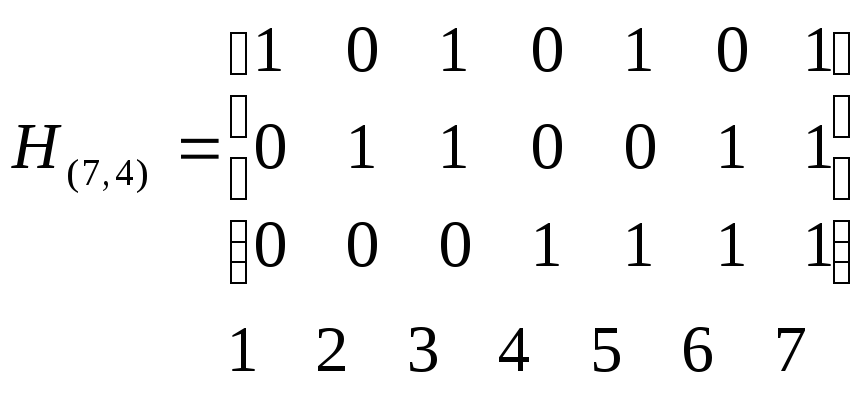 .
.
Из рассмотрения этой матрицы видно, что минимальное число линейно зависимых столбцов равно 3( к примеру 1, 2 и 3), следовательно, dmin=3.
В том случае, когда
столбцы матрицы H(n,k)– кода Хэмминга есть упорядоченная
записьm– разрядных
двоичных чисел, декодирование
осуществляется оригинальным образом.
В результате вычисления проверочного
соотношения для кодовой комбинации![]() ,
имеющей одиночную ошибку, получается
синдром
,
имеющей одиночную ошибку, получается
синдром![]() в точности равный номеру элемента, в
котором произошла ошибка.
в точности равный номеру элемента, в
котором произошла ошибка.
Действительно, если eiсодержит одну единицу в разряде, соответствующем ошибочному элементу, то при умножении на матрицуНТвсе строки матрицыНТ, соответствующие нулям вei, обращаются в нули, и лишь строка, соответствующая “1” вeiсохраняет свой вид (т.е. порядковый номер элемента в двоичной записи) в ответе.
Пример 5.15.Пусть приемник УЗО системы передачи
данных зарегистрировал комбинацию![]() .
Вычисление синдрома дает
.
Вычисление синдрома дает
 ,
,
т.е. ошибка в
четвертом элементе и кодовая комбинация
кода (7,4), которая была передана, имеет
вид:
![]()
Путем несложных преобразований из (n, k) – кода Хэмминга сdmin=3 можно получить (n+1, k) – код Хэмминга сdmin=4.
Для этого в кодовую комбинацию вводится избыточный элемент, являющийся результатом проверки на четность по всем элементам кодовой комбинации. Число информационных элементов остается прежним.
Матрица проверок для (n+1, k) – кода Хэмминга сdmin=4 получается из матрицы проверок (n, k) – кода сdmin=3 путем введения дополнительной строки из (n+1)-ой единицы.
Так как размерность
матрицы проверок кода с dmin=4
должна быть равна![]() ,
то к каждой строке матрицы проверок
кода сdmin=3,
необходимо добавить один нулевой элемент
для того, чтобы не нарушить введенные
ранее проверки. Матрица проверок для
(n+1, k)
– кодаdmin=4
имеет вид:
,
то к каждой строке матрицы проверок
кода сdmin=3,
необходимо добавить один нулевой элемент
для того, чтобы не нарушить введенные
ранее проверки. Матрица проверок для
(n+1, k)
– кодаdmin=4
имеет вид:
 ,
,
где H(n,k)= матрица проверок исходного кода сdmin=3.
Рассмотренная процедура, приведшая к удлинению кодовой комбинации на один разряд при увеличении dminна 1 единицу, получила названиеудлинениякода (1- удлинение).Удлинению могут быть подвергнуты и другие коды, например, коды Рида-Соломона.
Пример 5.16.Построить код Хэмминга (8,4) сdmin=4 на основе матрицы проверок кода (7,4).
Известно:

По виду матрицы
![]() можно сделать вывод о том, что в коде
(7,4) осуществляется 3 независимые проверки
на четность.
можно сделать вывод о том, что в коде
(7,4) осуществляется 3 независимые проверки
на четность.
Каждая из строк определяет элементы кодовой комбинации, охваченные одной проверкой.
Таким образом,
матрице
![]() соответствует следующая система
проверочных соотношений:
соответствует следующая система
проверочных соотношений:

Для того, чтобы получить код (8,4) с dmin=4 вводим еще одну проверку по всем элементам кодовой комбинации, а результат этой проверки записывается в виде дополнительного 8-го элемента:
![]()
или
![]() .
.
Этой проверке соответствует дополнительная (четвертая) строка в матрице Н(8,4), состоящая из восьми единиц. Для того чтобы не нарушить три предыдущие проверки на месте восьмого элемента в трех первых строках матрицыН(8,4)на месте восьмого элемента, проставляем нули. Итак, матрица проверок кода (8,4) получена в виде:
 .
.
Определим известным способом dmin(8,4) – кода. Из рассмотрения тех столбцов, сумма которых давала нулевой столбец в (7,4) – коде, видно, что с добавлением 4-ой строки они перестали быть линейно зависимыми. Теперь уже число линейно зависимых столбцов должно быть четным и минимум 4, например, 3 первые столбца и последний. Таким образом, для полученного кода Хэмминга (8,4)dmin=4.
До сих пор мы еще не разделили элементы кодовой комбинации на информационные и проверочные. Наиболее рационально, по-видимому, это можно сделать следующим образом. Желательно, чтобы каждое проверочное соотношение однозначно определяло проверочный элемент как результат проверки на четность некоторой совокупности информационных элементов. В таком случае мы получили бы возможность определять значение проверочного элемента наиболее простым образом – решением одного линейного уравнения с одним неизвестным. Для этого при упорядоченной записи столбцов матрицы H(n,k)в качестве проверочных элементов необходимо брать элементы с номерами 2i, гдеi изменяется от 0 доm-1, так как именно эти столбцы содержат только по одной единице. Последнее свидетельствует о том, что элементы с номерами 2iвходят только в одну проверку и, следовательно, они могут быть взяты в качестве проверочных.
Пример 5.17.Определить местоположение проверочных элементов к коде Хэмминга (7,4).
По виду матрицы
![]() ,
приведенной в предыдущем примере, в
качестве проверочных элементов выбираем
элементы, которым соответствуют столбцы,
содержащие только по одной единице,
т.е. первый, второй и четвертый.
Следовательно, 4 информационных элемента
кода (7,4) должны занимать места 3, 5, 6 и
7-го разрядов. Приведенная в предыдущем
примере система проверочных соотношений
позволяет определить значение каждого
из проверочных элементов по значениям
информационных элементов, т.е. по значению
элементов простого кода, который
необходимо закодировать кодом Хэмминга
,
приведенной в предыдущем примере, в
качестве проверочных элементов выбираем
элементы, которым соответствуют столбцы,
содержащие только по одной единице,
т.е. первый, второй и четвертый.
Следовательно, 4 информационных элемента
кода (7,4) должны занимать места 3, 5, 6 и
7-го разрядов. Приведенная в предыдущем
примере система проверочных соотношений
позволяет определить значение каждого
из проверочных элементов по значениям
информационных элементов, т.е. по значению
элементов простого кода, который
необходимо закодировать кодом Хэмминга

Зная места проверочных элементов, легко привести матрицу H(n,k)кода Хэмминга к канонической форме.
Для этого необходимо
столбцы с номерами 2i,
где![]() при упорядоченной записи столбцов
переместить на местаmпервых столбцов в порядке убывания
номеров. В общем виде такая перестановка
столбцов в матрицеH(n,k)приводит к эквивалентному (n,
k) – коду. В случае
же кодов Хэмминга естественной длины
код получается даже не эквивалентный,
а в точности совпадающий с исходным
кодом.
при упорядоченной записи столбцов
переместить на местаmпервых столбцов в порядке убывания
номеров. В общем виде такая перестановка
столбцов в матрицеH(n,k)приводит к эквивалентному (n,
k) – коду. В случае
же кодов Хэмминга естественной длины
код получается даже не эквивалентный,
а в точности совпадающий с исходным
кодом.
Пример 5.18.Преобразовать матрицу![]() к канонической форме.
к канонической форме.

Переставим столбцы: 4-ый на место 1-го, 1-ый на место 3-го, а 3-ий на место 4-го:
 .
.
Это и есть
каноническая форма матрицы
![]() .
Сравнение ее с исходной матрицей
.
Сравнение ее с исходной матрицей![]() показывает, что местам информационных
элементов в канонической форме
соответствуют столбцы с номерами 3, 5,
6, 7, а местам проверочных элементов -
столбцы 4, 2, 1.
показывает, что местам информационных
элементов в канонической форме
соответствуют столбцы с номерами 3, 5,
6, 7, а местам проверочных элементов -
столбцы 4, 2, 1.
При этом связи между информационными и избыточными элементами сохранились с учётом их перестановки:

Порождающую матрицуG(n, k) для кода Хэмминга можно получить из матрицыH(n,k), используя теорему 5.3:

Кодирующие и декодирующие устройства для этого класса кодов будут рассмотрены при изучении циклических кодов.
Оценим эффективность кодов Хэмминга.
а) Коды Хэмминга с dmin=3
Такие коды используются либо для исправления ошибки кратности t=1, либо для гарантийного обнаружения ошибок кратностиS=2. Соответственно, вероятность ошибки для этих случаев в канале с группированием ошибок равна:
![]() .
.
Выигрыш по достоверности по сравнению с простыми кодами той же длины составляет:
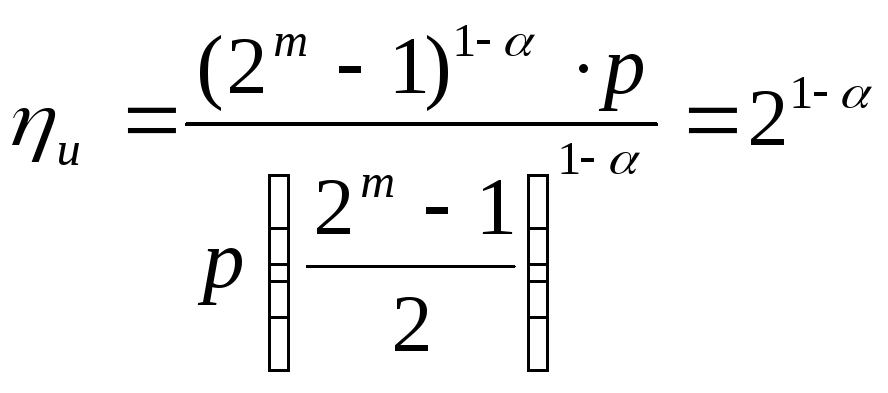

б) Коды Хэмминга с dmin=4.
Для таких кодов возможны два режима – исправление однократных ошибок и обнаружение ошибок и только обнаружение ошибок. Вероятность ошибки для этих режимов в случае группирования ошибок равна:
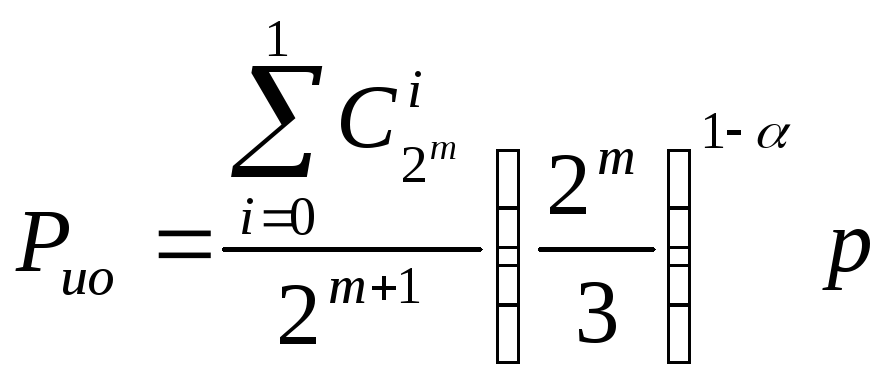
![]()
Выигрыш по достоверности по сравнению с простым кодом той же длины составляет:
![]() .
.
