
- •Предисловие
- •Благодарности
- •Как организована эта книга
- •Импульсные волны
- •Коррекционные волны
- •Базовые коррекционные формы
- •Составные коррекционные формы
- •Отношения Фибоначчи
- •Отклонения от математических пропорций
- •Подмена структур
- •Время
- •Импульсные волны
- •Первые волны
- •Третьи волны
- •Пятые волны
- •Растяжения
- •Принцип чередования
- •Каналы и линии тренда
- •Определение целей и задач
- •Иррегулярные коррекции
- •Горизонтальные треугольники
- •Зигзаги и двойные зигзаги
- •Диагональные треугольники
- •Подмена структур
- •Недостаток настойчивости и умственной честности
- •Неспособность проявить гибкость
- •Слишком выпуклое эго
- •Беспокойство
- •Скука
- •Нетерпеливость
- •Подготовка к созданию типичного плана трейдинга по Эллиотту
- •Часть 7. Пример реальной ситуации
- •Заключение

ЧастьII Важнейшие принципы |
Составные коррекционные формы |
Отношения Фибоначчи
1)Вот числа Фибоначчи: 1,1,2,3,5,8,13,21,34,55,89,144,233, 377, 610, и т.п.
2)Сумма любых двух соседних чисел равна следующему числу в последовательности. Пример: 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21; 13 + 21 = 34, и т.п.
3)Начиная с некоторого момента [After the first four digits - неясно, о каких digits говорит Балан - Mathematician], деление числа Фибоначчи на соседнее меньшее число дает отношение 1.618. Пример: 34/21=1.618. Далее, деление того же числа Фибоначчи на соседнее следующее дает нам отношение 0.618. Пример: 34/55 = 0.618.
4)Число, обратное отношению 1.618, равно 0.618. Аналогично, обратное числу 0.618 есть число 1.618. Пример: 1 /0.618 = 1.618, и 1 / 1.618 = 0.618.
5)Деление любого числа Фибоначчи на число, предшествующее ему на 2 позиции в последовательности, увеличивает отношение до 2.618. А деление того же числа на число, следующее за ним через 2 позиции в последовательности, приводит к отношению 0.382.
Пример: 55/144 = 0.382.
6)Число, обратное отношению 2.618, равно 0.382, а число, обратное пропорции 0.382, равно 2.618. Пример: 1 /2.618 = 0.382; 1 / 0.382 = 2.618.
7)Деление любого числа Фибоначчи на число, предшествующее ему на три позиции в последовательности, дает отношение 4.236. Пример: 144/34 = 4.236. А деление того же числа на число, следующее за ним через 3 позиции в последовательности, дает отношение 0.236. Пример: 144/610 = 0.236. 8) Число, обратное отношению 4.236, равно 0.236, а число, обратное пропорции 0.236, равно 4.236. Пример: 1 /4.236 = 0.236; 1 / 0.236 = 4.236.
9)Отношение, равное 1 (равенство), выражает отношение равенства между двумя первыми числами в последовательности Фибоначчи; таким образом, 1/1 = 1. Отношение
0.5выступает как соотноошение между вторым и третьим числами в последовательности; следовательно, 1/2 = 0.5.
10)Числа Фибоначчи как таковые не имеют ценности при предсказании «протяженности» рыночных движений в смысле абсолютных значений цены и времени. Ключевые элементы - отношения между числами в последовательности. Эллиотт считает, что эти пропорции являются «первичными детерминантами», определяющими «протяженность» цены и времени на любом рынке.
11)Чаще и надежнее всего отношения Фибоначчи обнаруживаются скорее между перемежающимися волнами, чем между соседними. К примеру, на длину волны 3 в пятиволновке влияет скорее длина волны 1, чем длина волны 2.
12)Целевые ориентиры [targets], вычисленные с помощью отношений Фибоначчи, обычно проявляются в качестве важных уровней поддержки и сопротивления - даже в том случае, если после этого происходит их пробой.
13)Важным дополнением к Волновому принципу Эллиотта оказывается понимание того, что пропорции Фибоначчи являются «первичными детерминантами», определяющими «протяженность» цены и времени на рынке. Волновой принцип Эллиотта предоставляет нам форму и структуру, а отношения Фибоначчи дают инструмент для измерения потенциала любого ценового движения, включая и границы [time windows, "временные окна" - Mathematician] вероятных сроков окончания этих движений. Это очень мощное сочетание.
31
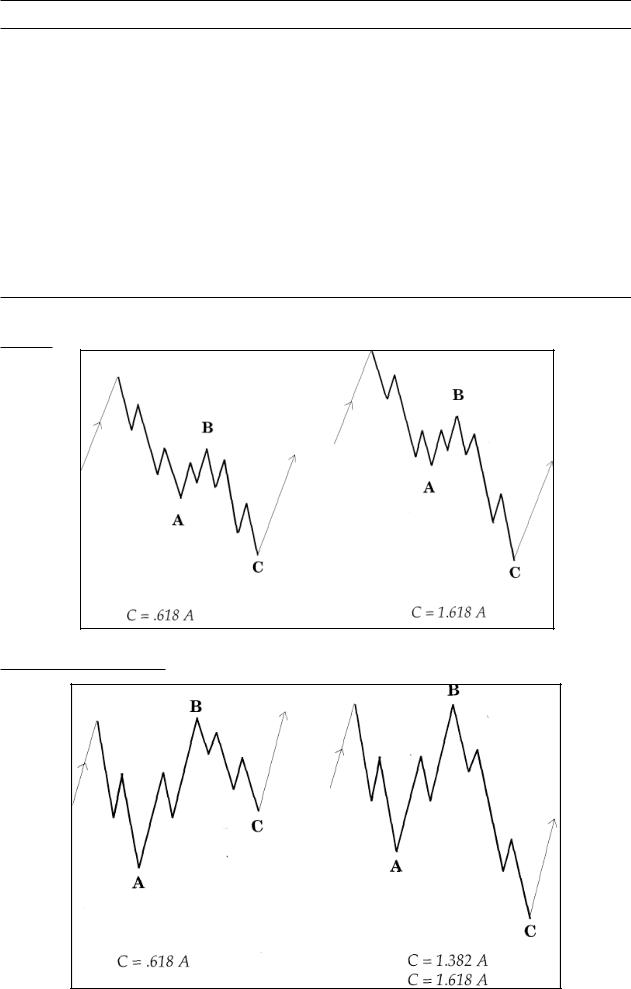
Часть III Отклонения
Отклонения от нормы в волновом анализе скорее представляются правилом, чем исключением. Трудность в этом смысле проистекает из двух причин:
1)Отклонение от математических отношений (пропорций) между частями структуры. Примеры отклонений такого типа можно видеть на стр. III-1 è III-2.
2)Подмена коррекционных структур простого типа одной или несколькими сложными. Читатель уже должен понять по предыдущим примерам, что трудность предсказания
момента окончания коррекционной структуры возрастает вместе с количеством базовых структур, объединяющихся вместе. Проблема еще больше усложняется из-за того, что любая из базовых «коррекционных» структур может включать в своей собственной коррекционной волне формы, состоящие из еще более сложных фигур, типа иррегулярной коррекции, плоской коррекции или треугольника. Следующие примеры иллюстрируют это утверждение:
Отклонения от математических пропорций
Зигзаг
Плоская коррекция
32
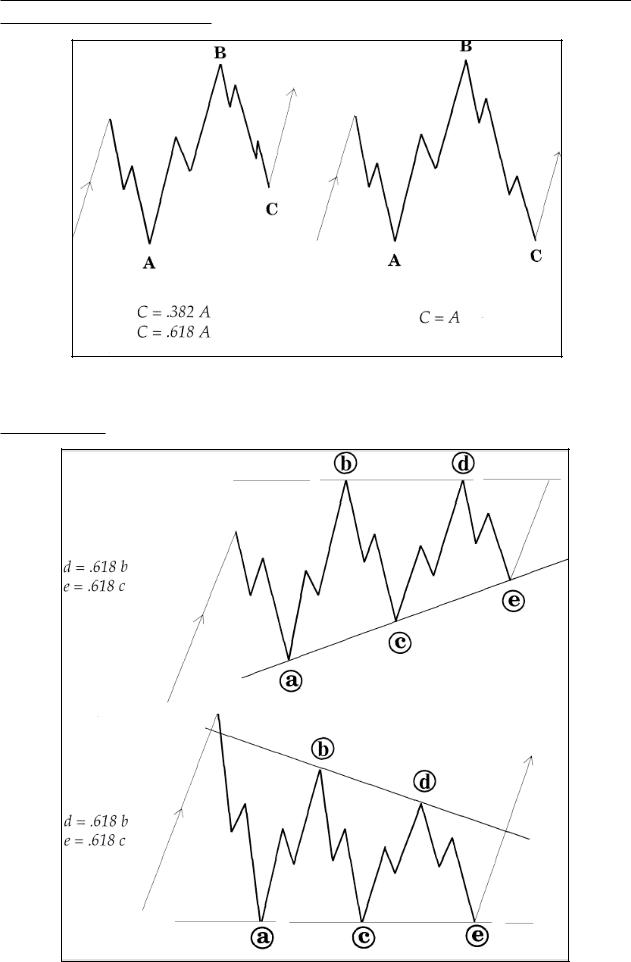
Часть III Отклонения |
Отклонения от математических пропорций |
Иррегулярная коррекция
[соотношения внизу не соответствуют нарисованным - Mathematician]
Треугольник
33
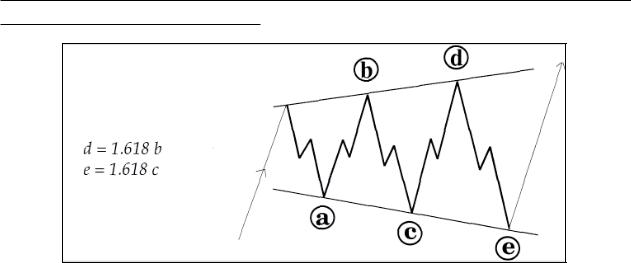
Часть III Отклонения |
Отклонения от математических пропорций |
Расширяющийся треугольник
34
