Случайные события 3

§3. СЛУЧАЙНЫЕ СОБЫТИЯ

При установке порядка появились имена. Поскольку возникли имена, нужно знать предел их употребления. Знание предела позволяет избавиться от опасности.

Лао Цзы

Пусть проводится некоторый опыт со случайным исходом.

Определение 3.1. Множество всех возможных взаимоисключающих исходов данного опыта (испытания, эксперимента) называется пространством элементарных событий, а сами исходы – элементарными событиями (исходами).

Определение 3.2. Случайным событием (или просто: событием) называется такой исход опыта (испытания, эксперимента, наблюдения), который может произойти или не произойти. События обозначаются, как правило, заглавными буквами латинского алфавита: А,В,С,D...

С точки зрения теории множеств, случайным событием является любое подмножество множества . Элементарные события, входящие в подмножество А пространства называются благоприятствующими событию А.

Определение 3.3. Событие называется достоверным, если оно обязательно наступит в результате данного опыта (очевидно, что – достоверное событие).

Событие называется невозможным, если оно заведомо не произойдет в результате проведения опыта; невозможное событие обозначается через ∅.

Пример 3.1. Задумчивый философ подбросил один раз игральную кость и посмотрел на число очков, выпавших на ее верхней грани. Пространство элементарных событий, описывающих этот эксперимент, можно представить как , где элементарный исход – выпадение i очков. Тогда событие А (число очков кратно трем) представимо как , событие В (число очков нечетно) имеет вид , событие С (число очков больше трех) есть . Событие D (число очков меньше семи) является достоверным, событие Е (число очков дробно) – невозможным.

Определение 3.4. Суммой событий А и В называется событие А+В, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А и В (т.е.или А, или В, или оба вместе).

Произведением событий А и В называется событие А∙В, которое происходит тогда и только тогда, когда происходят оба события А и В (т.е. и А и В вместе).

Разностью событий А и В называется событие А–В, которое происходит тогда и только тогда, когда происходит событие А, но не происходит В.

Событие А влечет событие В (или А является частным случаем В), если из того, что происходит событие А, следует наступление события В (обозначается АВ).

События А и В называются равными, если АВ и ВА (обозначается А=В).

Противоположным событию А называется событие , которое происходит тогда и только тогда, когда не происходит событие А.

Определение 3.5. Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте (А∙В=∅); в противном случае события называются совместными.

События A₁, A₂,…,A_n называются попарно-несовместными, если любые два них несовместны (A_i∙A_j=∅, ij, 1i,jn).

Определение 3.6. События A₁,A₂,…,A_n образуют полную группу, если в результате опыта непременно должно произойти хотя бы одно из них (A₁+A₂+…+A_n=).

Пример 3.2. Три студента независимо друг от друга решают одну и ту же задачу. Пусть событие А_i – i-ый студент решил задачу (i = 1, 2, 3). Представьте c помощью операций над событиями А_i и следующие события:

а) А – все студенты решили задачу;

б) В – задачу решил только первый студент;

в) С – задачу решил хотя бы один студент;

г) D – задачу решил только один студент.

Решение. а) Осуществление события А означает, что произошли события А₁, А₂ и А₃ одновременно, т.е. А = А₁∙А₂∙А₃.

б) В этом случае событие А₁ произошло, а события А₂ и А₃ не произошли, т.е. произошли события и . Следовательно, В = ∙∙.

в) Событие С означает, что произошло или событие А₁, или событие А₂, или событие А₃, или любые два из них, или все вместе, т.е. имеем сумму событий: С = А₁+А₂+А₃.

г) Задачу решит только первый студент ∙∙, или только второй студент ∙∙, или только третий студент ∙∙, т.е. имеем сумму событий D = ∙∙+∙∙+∙∙.

Пример 3.3. Штирлиц договорился с пастором Шлагом о встрече в кафе «Элефант» между 11 и 12 часами. Каждый приходит в случайный момент указанного промежутка времени и ждет другого до истечения часа, но не более 15 минут, после чего уходит. Наблюдаемый результат – пара чисел (x;y), где x – время прихода Штирлица, y – время прихода пастора Шлага. Постройте множество элементарных исходов и его подмножество А, соответствующее событию «встреча состоялась».

Решение. Множество элементарных исходов представляет собой пары чисел, каждое из которых принадлежит отрезку [0;60]: . Графически это множество можно представить как квадрат размером 6060 в первой четверти прямоугольной системы координат (см. рис.3.1,а). Чтобы встреча состоялась, разница во времени прихода Штирлица и пастора Шлага не должна составлять более 15 минут, причем не важно, кто из них пришел первым. Это соотношение между x и y можно описать неравенством , поэтому событие «встреча состоялась» можно представить как А=. Неравенство заменим двойным неравенством или системой неравенств 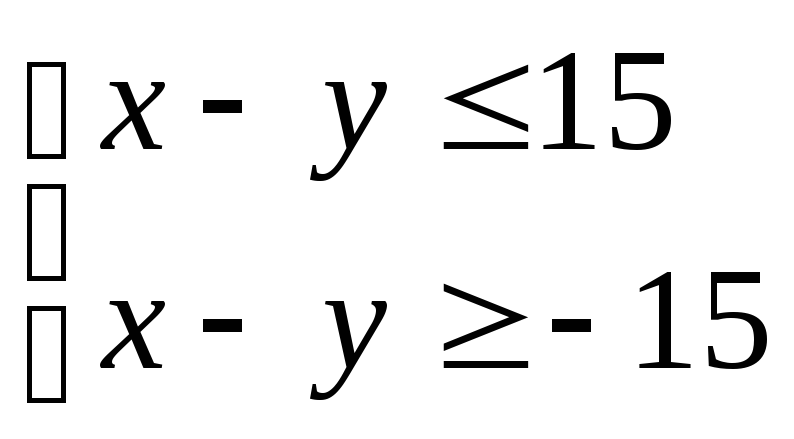, которая сводится к системе 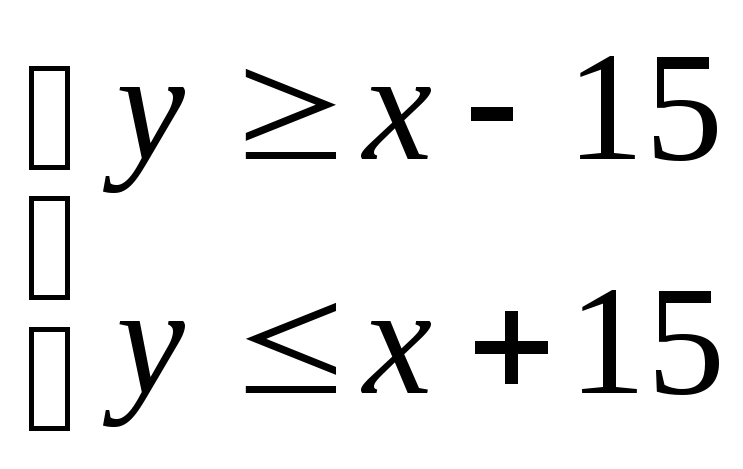. Множество решений полученной системы графически представляет собой полосу в системе координат. Т.о. состоявшуюся встречу можно графически изобразить так, как это сделано на рис.3.1(б).

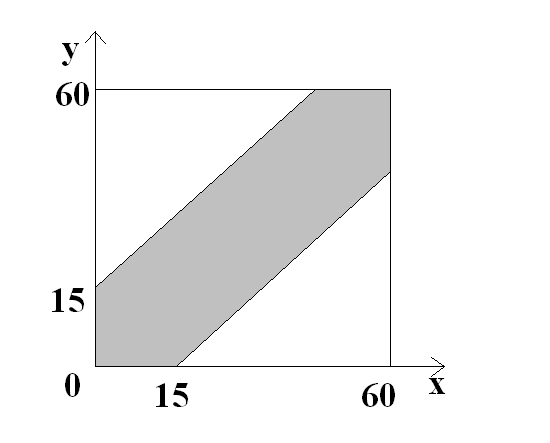
Рис.3.1(а) Рис.3.1(б)

Решите задачи:

1. Постройте пространство элементарных событий для следующих испытаний:

а) проводится одна игра в шахматы;

б) трижды подбрасывается монета;

в) подбрасывается три монеты: золотая, серебряная и бронзовая;

г) дважды подбрасывается игральная кость;

д) подбрасывается игральная кость, а затем монета.

2. В урне лежат четыре шара с номерами от 1 до 4. Из урны наудачу последовательно извлекают два шара (без возвращения). Составьте пространство элементарных событий для этого опыта, если его элементами служат:

а) двузначные числа, образованные номерами извлеченных шаров;

б) суммы номеров извлеченных шаров.

3. Образуют ли полную группу следующие группы событий:

а) Опыт – бросание монеты; события:

А₁ – появление герба; А₂ – появление цифры.

б) Опыт – бросание двух монет; события:

В₁ – появление двух гербов; В₂ – появление двух цифр.

в) Опыт – два выстрела по мишени; события:

А₀ – ни одного попадания;

А₁ – одно попадание;

А₂ – два попадания.

г) Опыт – два выстрела по мишени; события:

С₁ – хотя бы одно попадание; С₂ – хотя бы один промах.

д) Опыт – вынимание карты из колоды; события:

D₁ – появление карты червонной масти;

D₂ – появление карты бубновой масти;

D₃ – появление карты трефовой масти?

4. Являются ли несовместными следующие события:

а) Опыт – бросание монеты; события:

А₁ – появление герба; А₂ – появление цифры.

б) Опыт – бросание двух монет; события:

В₁ – появление герба на первой монете;

В₂ – появление цифры на второй монете.

в) Опыт – два выстрела по мишени; события:

С₀ – ни одного попадания;

С₁ – одно попадание;

С₂ – два попадания.

г) Опыт – два выстрела по мишени; события:

D₁ – хотя бы одно попадание; D₂ – хотя бы один промах.

д) Опыт – вынимание двух карт из колоды; события:

Е₁ – появление двух черных карт;

Е₂ – появление туза;

Е₃ – появление дамы?

5. Являются ли равновозможными следующие события:

а) Опыт – бросание «правильной» монеты; события:

А₁ – появление герба; А₂ – появление цифры.

б) Опыт – бросание «неправильной» (погнутой) монеты; события:

В₁ – появление герба; В₂ – появление цифры.

в) Опыт – выстрел по мишени; события:

С₁ – попадание; С₂ – промах.

г) Опыт – бросание двух монет; события:

D₁ – появление двух гербов;

D₂ – появление двух цифр;

D₃ – появление одного герба и одной цифры.

д) Опыт – вынимание одной карты из колоды; события:

Е₁ – появление карты червонной масти;

Е₂ – появление карты бубновой масти;

Е₃ – появление карты трефовой масти.

е) Опыт – бросание игральной кости; события:

F₁ – появление не менее трех очков;

F₂ – появление не более четырех очков?

6. Назовите противоположные события для следующих событий:

А – выпадение двух гербов при бросании двух монет;

В – появление белого шара из урны, в которой белые, черные и красные шары;

С – три попадания при трех выстрелах;

D – хотя бы одно попадание при пяти выстрелах;

Е – не более двух попаданий при пяти выстрелах;

F – выигрыш первого игрока при игре в шахматы;

G – покупка товара не произойдет ни в одном из трех магазинов;

H – в семейной паре муж старше жены.

7. Опыт состоит в бросании двух монет, золотой и серебряной. Рассматриваются следующие события:

А – появление герба на золотой монете;

В – появление цифры на золотой монете;

С – появление герба на серебряной монете;

D – появление цифры на серебряной монете;

Е – появление хотя бы одного герба;

F – появление хотя бы одной цифры;

G – появление одного герба и одной цифры;

H – непоявление ни одного герба;

К – появление двух гербов.

Определите, каким событиям этого списка равносильны следующие события: 1) A+C; 2) А∙С; 3) E∙F; 4) G+E; 5) G∙E; 6) B∙D; 7) Е+К.

8. По мишени производится три выстрела. Рассматриваются события А_i– попадание при i-м выстреле (i = 1, 2, 3). Представьте c помощью операций над событиями А_i и следующие события:

А – все три попадания;

В – все три промаха;

С – хотя бы одно попадание;

D – хотя бы один промах;

Е – не меньше двух попаданий;

F – не больше одного попадания;

G – попадание в мишень не раньше, чем при третьем выстреле.

9. Биолог наблюдает в микроскоп четыре однотипных клетки. Каждая из них за время наблюдения может разделиться или не разделиться. Рассматриваются события:

А – разделится ровно одна из четырех клеток;

В – разделится хотя бы одна клетка;

С – разделится не менее двух клеток;

D – разделится ровно две клетки;

Е – разделится ровно три клетки;

F – разделится все четыре клетки.

В чем состоят события:

1) А+В; 2) А∙В; 3) В+С; 4) В∙С; 5) D+E+F; 6) B∙F.

Совпадают ли события B∙F и C∙F? Совпадают ли события В∙С и D?

10. На рисунках 3.2(а–г) изображены электрические схемы. Выключатели изображены кружками, в которых указан номер выключателя. Запишите через события А_i – «выключатель с номером i включен» для каждой схемы события А – «ток идет» и — «ток не идет».

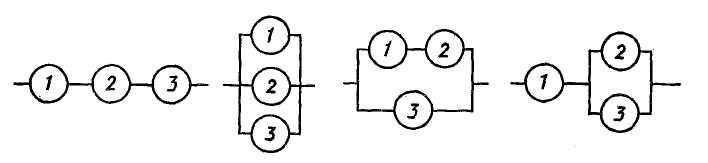
Рис.3.2(а) Рис.3.2(б) Рис.3.2(в) Рис.3.2(г)

11. Прибор состоит их двух блоков. Первый блок состоит из двух однотипных деталей и работает при исправности хотя бы одной из них. Второй блок состоит из трех однотипных деталей и работает при исправности хотя бы двух их них. Весь прибор работает, если работают оба блока. Рассматриваются следующие события:

А_i – работает i-ая деталь первого блока (i = 1, 2);

B_j – работает j-ая деталь первого блока (j = 1, 2, 3).

Представьте c помощью операций над событиями А_i, B_j и их отрицаниями следующие события:

С – работает первый блок;

D – работает второй блок;

Е – не работает первый блок;

F – не работает второй блок;

G – прибор работает;

H – прибор не работает;

I – прибор не работает, но чтобы его исправить, достаточно заменить одну деталь.

12. Производится стрельба по прямоугольной мишени: –2x2, –1y1. Результат – координаты точки попадания. Промахи исключены. Рассматриваются события:

А – ордината точки попадания положительна;

В – абсцисса точки попадания не меньше ее ординаты;

С – произведение координат точки попадания неотрицательно.

Задайте множество элементарных исходов и подмножества, соответствующие указанным событиям, аналитически и графически.

13. В примере 3.3 о встрече Штирлица и пастора Шлага опишите аналитически и графически следующие события:

В – Штирлиц ждал пастора Шлага все обусловленное время и не дождался;

С – пастору Шлагу не пришлось ждать Штирлица;

D – встреча состоялась после половины двенадцатого;

Е – пастор Шлаг опоздал на встречу;

F – встреча состоялась, когда до истечения часа оставалось меньше пяти минут.