3.3. Стационарные характеристики смо

На основе полученных значений вероятностей пребывания системы в состояниях определяем показатели эффективности стационарного режима:

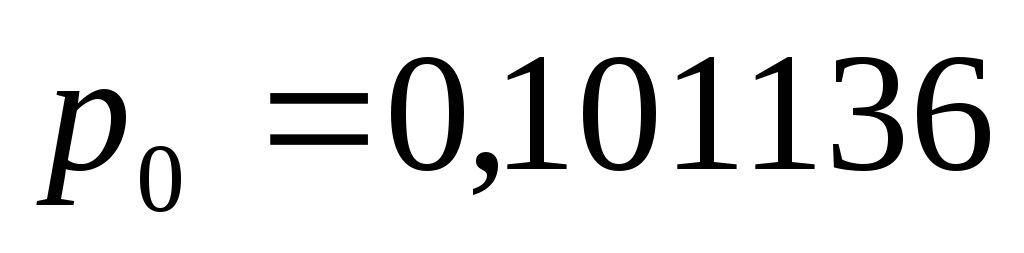• –вероятность того, что машина не работает;

• –вероятность того, что машина занята рубкой;

• –вероятность того, что машина занята рубкой и одно бревно ожидает в очереди;

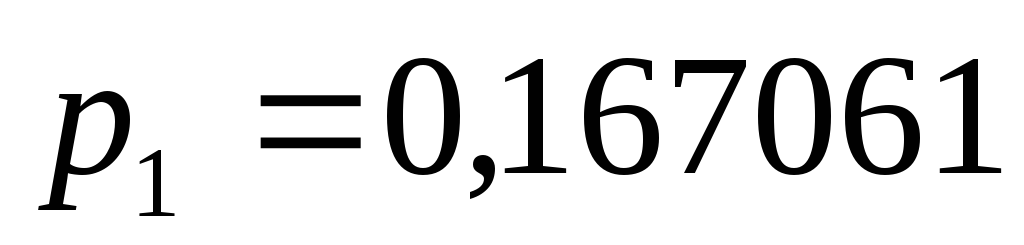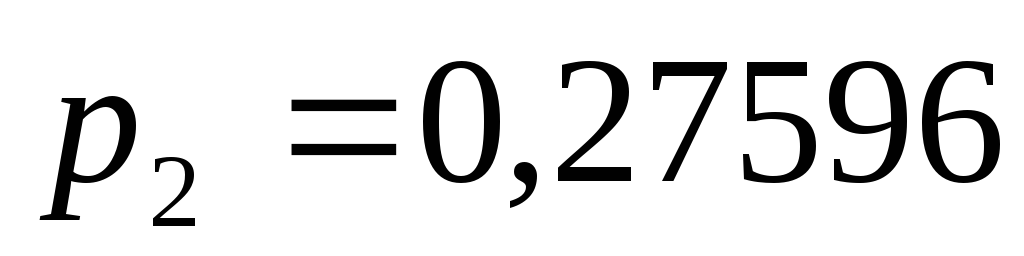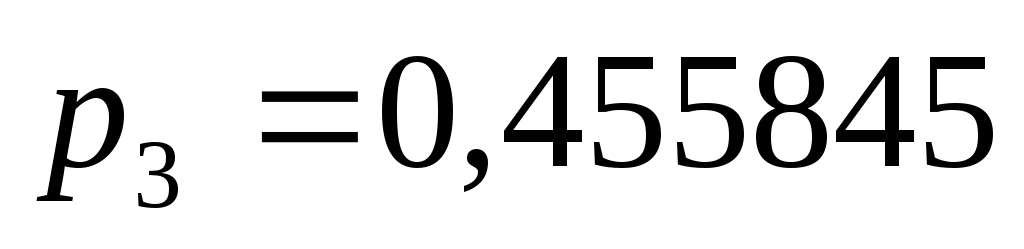• –вероятность того, что машина занята рубкой и два бревна ожидают в очереди.

Рассмотрим другие показатели эффективности работы системы массового обслуживания.

Пусть – число машин, занятых рубкой. Это есть случайная величина с возможными значениями: 0, 1. Вероятности этих значений соответственно равны

,

.

Тогда среднее число машин, занятых рубкой, есть математическое ожидание случайной величины , которое равно

.

Следовательно, среднее число работающих машин равно 0,90.

Пусть – число машин, свободных от рубки. Это есть случайная величина с возможными значениями: 0, 1. Вероятности этих значений соответственно равны

,

.

Тогда среднее число машин, свободных от рубки, есть математическое ожидание случайной величины , которое равно

.

Следовательно, среднее число простаивающих машин равно 0,10. Общее число занятых и свободных от рубки машин равно

.

Коэффициент загрузки машин равен отношению среднего числа загруженных машин к общему числу машин в цехе, т.е.

.

Тогда в процентах .

Коэффициент простоя машин равен отношению среднего числа машин, свободных от рубки, к общему числу машин в цехе, т.е.

.

Тогда в процентах .

Пусть – число бревен в очереди. Это есть случайная величина с возможными значениями: 0, 1,2. Вероятности этих значений соответственно равны

,

,

.

Тогда среднее бревен в очереди есть математическое ожидание случайной величины , которое равно

.

Таким образом, среднее число бревен, находящихся в очереди на рубку, равно 1,19, т.е. более одного бревна.

3.4.Математическая модель нестационарного режима

Обозначим через вероятность пребывания системы в момент временив состоянии,. Это – переходные вероятности, изменяющиеся со временем. Согласно правилу, нестационарный режим описывается следующей системой дифференциальных уравнений, составленной по графу состояний, изображенному на рис.4:

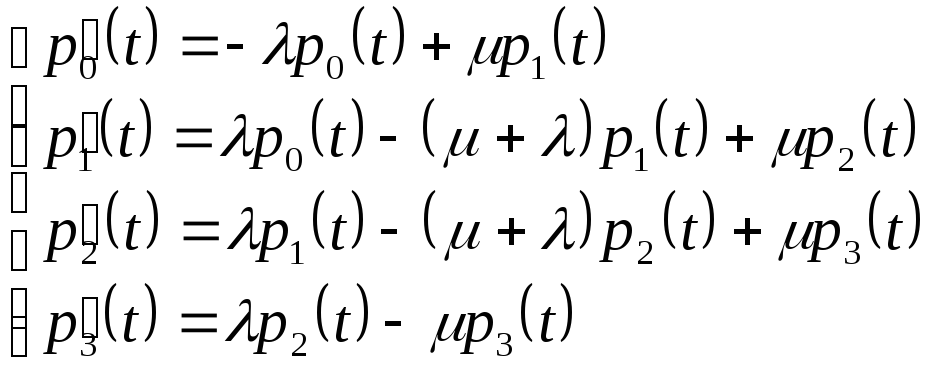. (14)

Решение этой системы должно удовлетворять начальному условию

, , (15)

означающему, что в момент времени система находится в состоянии: бревен в цехе нет, рубительные машины простаивают и очередь отсутствует. Контролем правильности решения системы является условие нормировки

, (16)

которое означает, что для любого момента времени сумма вероятностей постоянна и равна .

Решение задачи (14)-(15) получим в Excel на Листе 2 методом Эйлера, как показано в табл.6.

Таблица 6

	A	B	C	D	E		F		G	Н
1		4,46	Решение системы дифференциальных уравнений
2		2,7	t							
3	h	0,1	0	1	0	0		0		1
4			0,1	0,554	0,446	0		0		1
5			0,2	0,427336	0,373748	0,198916		0		1
6			0,3	0,337656104	0,350444	0,223183752		0,08871654		1
7			0,4	0,281681256	0,31038	0,243635499		0,16430302		1
8			0,5	0,239854075	0,279559	0,251983877		0,22860264		1
…			…	…	…	…		…		…
79			7,6	0,101135415	0,167061	0,275959559		0,45584431		1
80			7,7	0,101135415	0,167061	0,275959559		0,45584431		1

В ячейки B1 и B2 поместим значения интенсивностей и. В ячейкуB3 поместим значение шага интегрирования . Примем. Блок ячеекC3 : G3 зарезервируем для записи времени начала функционирования системы и начальных вероятностей, взятых из (15). В блоке ячеекC4 : G4 поместим формулы Эйлера, по которым рассчитываются вероятности для текущего момента времени по известным вероятностям для предыдущего момента времени. Эти формулы приведены в табл.7.

Таблица 7

C4	C3 + $B$3
D4	D3 + $B$3 * (-$B$1 * D3 + $B$2 * E3)
E4	E3 + $B$3 * ($B$1 * D3 – ($B$2 + $B$1) * E3 + $B$2 * F3)
F4	F3 + $B$3 * ($B$1 * E3 – ( $B$2 + $B$1) * F3 + $B$2 * G3)
G4	F3 + $B$3 * ($B$1 *F 3 – $B$2 *G 3)

Протягивая эти формулы вниз, получим решение системы уравнений.

В табл.6 колонка I служит для контроля правильности введенных соотношений, а также для контроля правильности выбора шага интегрирования. В клетку I3 запишем формулу

= СУММ( D3 : G3 ),

которую протянем вниз. Для принятого шага элементы этой колонки равны «единице». А это означает правильность решения системы дифференциальных уравнений (14).

Вероятности с ростом временистремятся к своим стационарным значениям, не зависящим от времени и полученным в п.3.2. Поэтому, таблицу вероятностей вычисляем, пока ни будут выполняться соотношения:

, ,,.

Как следует из табл.2, указанные соотношения выполняются с точностью до трех знаков после запятой уже для момента времени .

Графическая иллюстрация вероятностей из табл.6 приведена на рис.5.

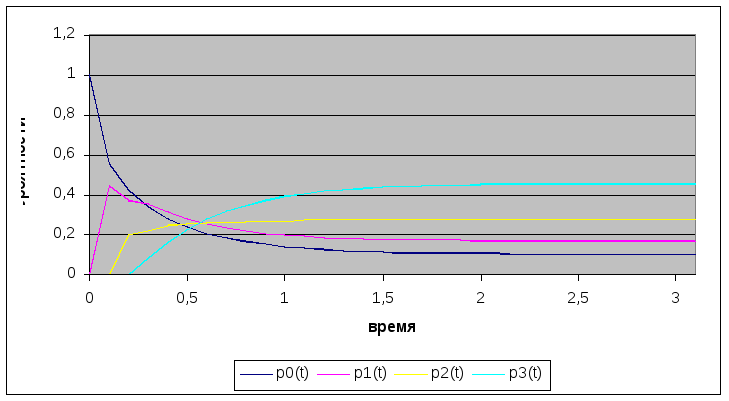
Рис.5. Вероятности состояний системы

Рис.5 свидетельствует о достаточно быстром вхождении процесса в стационарный режим, при котором вероятности практически не изменяются, а графики становятся параллельными оси времени.