3.Выполнения лабораторной работы

Исходные данные в табл.1.

Таблица 4

4,46	2,7	1	2

Согласно принятой выше кодировке рассматриваемая система относится к классу .

3.1. Граф состояний

Перечислим возможные состояния системы:

–в системе бревен нет, машина свободна от рубки;

–в системе 1 бревно, машина занята рубкой;

–в системе 2 бревна, машина занята рубкой, одно бревно находится в очереди;

–в системе 3 бревна, машина занята рубкой, два бревна находится в очереди.

Граф состояний приведен на рис.4. Переходы слева направо связаны с поступлением в систему очередного бревна, поэтому все интенсивности переходов одинаковы и равны . Переходы справа налево обусловлены окончанием рубки бревна. Во всех состояниях работает одна машина, поэтому интенсивность перехода из состояния в состояние одинаково и равно.

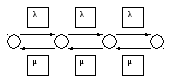
Рис.4. Граф состояний системы

Очевидно, что данный граф описывает процесс размножения и гибели. Поэтому для него справедливы все соотношения п.2.4

3.2. Математическая модель стационарного режима

Пусть – стационарная вероятность пребывания системы в состоянии,. Тогда имеет место следующая система алгебраических уравнений, описывающая стационарный режим:

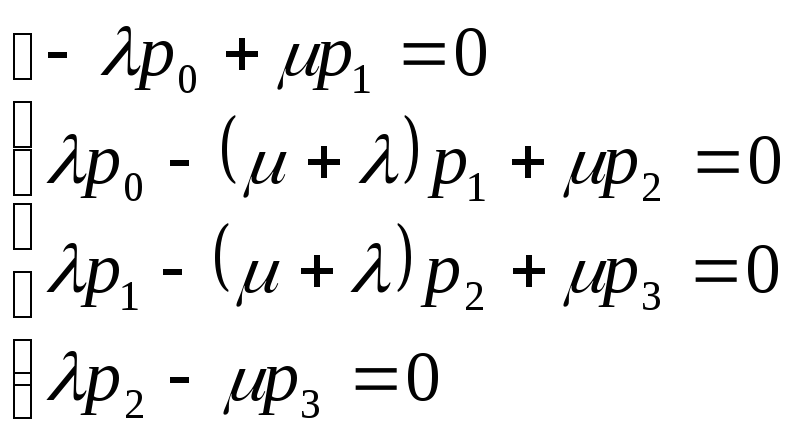(12)

Эту систему следует решать вместе с условием нормировки

. (13)

Воспользуемся для этой цели электронной таблицей Excel. На Листе 1, как показано в табл.5, в ячейки B1 и B2 поместим значения интенсивностей и. Блок ячеекD3 : G3 зарезервируем для записи значений искомых вероятностей (эти ячейки сначала пустые). В блоке ячеекD4 : G6 поместим коэффициенты при неизвестных системы (12), за исключением последнего уравнения. Последнее уравнение системы (12) заменим условием нормировки (13), тогда в блоке ячеек D7 : G7 будут располагаться «единицы».

Таблица 5

	4,46		Решение системы алгебраических уравнений
	2,7
			0,101136	0,167061	0,27596	0,455845
			-4,46	2,7	0	0	-4,1E-09	0
			4,46	-7,16	2,7	0	-4,3E-08	0
			0	4,46	-7,16	2,7	-7E-08	0
			1	1	1	1	1,000001

Блок ячеек I4 : I7 содержит формулы для записи левых частей системы уравнений (10) и (11), а именно, в клетку I4 поместим формулу

= СУММПРОИЗВ( $D$3 : $G$3 ; D4 : G4 ),

которую протянем на блок ячеек I5 : I7. В блоке ячеек J4 : J6 содержатся правые части системы (12), равные «нулям».

Обращение к процедуре «Поиск решения» позволит найти решение системы уравнений (12). Для этого в появившемся окне указываем:

• целевую ячейку, в данном случае I7, равную значению 1 (условие нормировки);

• изменяемые ячейки, в данном случае блок D3 : G3;

• ограничение, в данном случае I4 : I6 = J4 : J6.

Нажимаем «Выполнить» в блоке D3 : H3 получим решение системы уравнений. Таким образом, стационарные вероятности равны, , , .