2 курс Бакалавр экономики / Теория вероятностей и математическая статистика / Экз. вопросы по Теории вероятностей 2011-2012 год

Экзаменационные вопросы по дисциплине

«Теория вероятностей и математическая статистика» для студентов бакалавриата 2 курса, обучающихся по направлениям «Экономика» и «Менеджмент», на 2011-2012 год

1. Полная группа событий. Противоположные события. Соотношение между вероятностями событий, образующих полную группу; примеры противоположными событиями.

2. Формулы полной вероятности и Байеса (с выводом). Примеры.

3. Линейная парная регрессия. Система нормальных уравнений для определения параметров прямых регрессий. Выборочная ковариация. Формулы для расчета коэффициентов регрессии.

4. Оценка генеральной средней по собственно-случайной выборке. Несмещенность и состоятельность выборочной средней.

5. Оценка генеральной доли по собственно-случайной выборке. Несмещенность и состоятельность выборочной доли.

6. Формула доверительной вероятности при оценке доли признака. Средняя квадратическая ошибка повторной и бесповторной выборок при оценке генеральной доли признака.

7. Определение необходимого объема повторной и бесповторной выборок (при оценке генеральной средней и доли).

8. Математическое ожидание дискретной случайной величины и его свойства (одно из них доказать).

9. Математические операции над дискретными случайными величинами. Приведите пример построения закона распределения случайной величины Z=X+Y или Z=XY по заданным распределениям Х и Y.

10. Дисперсия дискретной случайной величины и ее свойства (одно из них доказать).

11. Статистическое определение вероятности события и условия его применимости. Пример.

12. Оценка генеральной дисперсии по собственно-случайной выборке. Смещенность и состоятельность выборочной дисперсии (без вывода). Исправленная выборочная дисперсия.

13. Функция распределения случайной величины, ее свойства и график.

14. Непрерывная случайная величина (НСВ). Вероятность отдельно взятого значения НСВ. Математическое ожидание и дисперсия НСВ.

15. Математическое ожидание и дисперсия числа m и частости m/n наступлений события в п повторных независимых испытаниях (с выводом).

16. Случайная величина, распределенная по биномиальному закону, ее математическое ожидание и дисперсия (привести пример). Закон распределения Пуассона.

17. Центральная предельная теорема. Понятие о теореме Ляпунова и ее значение. Пример.

18. Статистическая гипотеза и статистический критерий. Ошибка 1-го и 2-го рода. Уровень значимости и мощность критерия. Принцип практической уверенности.

19. Оценка тесноты связи. Выборочный коэффициент корреляции, его определение и свойства.

20. Понятие двумерной (n-мерной) случайной величины. Примеры. Таблица ее распределения. Условные распределения и их нахождение по таблице распределения.

21. Понятие о двумерном нормальном законе распределения. Условные математические ожидания и дисперсии.

22. Ковариация и коэффициент корреляции случайных величин. Связь между некоррелированностью и независимостью случайных величин.

23. Вариационный ряд, его разновидности. Средняя арифметическая и дисперсия ряда. Упрощенный способ их расчета.

24. Генеральная и выборочная совокупности. Принцип образования выборки. Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Основная задача выборочного метода.

25. Понятие об оценке параметров (характеристик) генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность.

26. Понятие об интервальном оценивании. Доверительная вероятность и доверительный интервал. Предельная ошибка выборки. Ошибки репрезентативности выборки (случайные и систематические).

27. Формула доверительной вероятности при оценке генеральной средней. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной средней.

28. Построение теоретического закона распределения по опытным данным. Понятие о критериях согласия.

29. Критерий согласия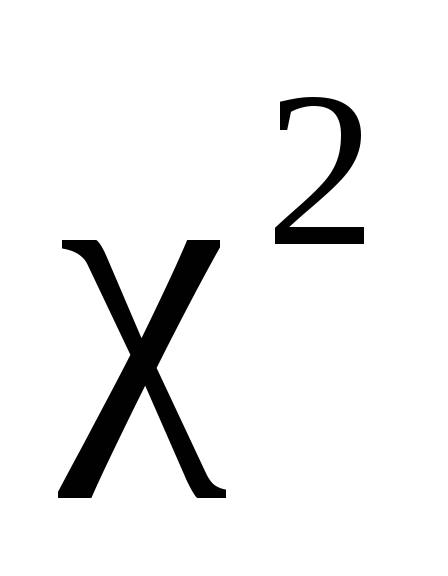- Пирсона и схема его применения.

30. Функциональная, статистическая и корреляционная зависимости. Различия между ними. Основные задачи теории корреляции.

31. Несовместные и совместные события. Сумма событий. Теорема сложения вероятностей (с доказательством). Привести пример на применение теоремы сложения вероятностей.

32. Зависимые и независимые события. Произведение событий. Условная вероятность. Теорема умножения вероятностей (с доказательством). Привести пример применения теоремы умножения вероятностей.

33. Лемма Чебышева (неравенство Маркова) (с доказательством для дискретной случайной величины). Привести примеры её применения.

34. Неравенство Чебышева (с выводом) и его частные случаи для случайной величины, распределенной по биномиальному закону, и для частости события.

35. Неравенство Чебышева для средней арифметической случайных величин. Теорема Чебышева (с доказательством) и ее значение. Пример.

36. Определение нормального закона распределения. Теоретико-вероятностный смысл его параметров: нормальная кривая и зависимость ее положения и формы от параметров.

37. Функция распределения нормально-распределенной случайной величины и ее выражение через функцию Лапласа Ф(х).

38. Формулы для определения вероятностей: а) попадания нормально распределенной случайной величины в заданный интервал; б) ее отклонения от математического ожидания. Правило трех сигм.

39. Повторные независимые испытания. Формула Бернулли (с выводом). Привести пример её применения.

40. Локальная теорема Муавра—Лапласа и условия ее применимости. Функция Гаусса f(x) и её свойства. Привести пример использования локальной теоремы Муавра – Лапласа.

41. Асимптотическая формула Пуассона и условия ее применимости. Привести пример использования формулы Пуассона.

42. Интегральная теорема Муавра—Лапласа и условия ее применимости. Функция Лапласа Ф(х) и ее свойства. Привести пример использования интегральной теоремы Муавра – Лапласа.

43. Плотность вероятности непрерывной случайной величины, ее определение и свойства. Кривая распределения. Связь между функцией распределения и плотностью вероятности непрерывной случайной величины. Математическое ожидание и дисперсия непрерывной случайной величины.

44. Следствия из интегральной теоремы Муавра—Лапласа (одно с выводом). Примеры.

45. Понятие случайной величины и ее описание. Дискретная случайная величина и ее закон (ряд) распределения. Независимые случайные величины. Привести примеры.

46. Закон больших чисел. Теорема Бернулли (с доказательством) и ее практическое значение.

47. Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события. Непосредственный подсчет вероятности. Привести примеры.

48. Разложение общей суммы квадратов 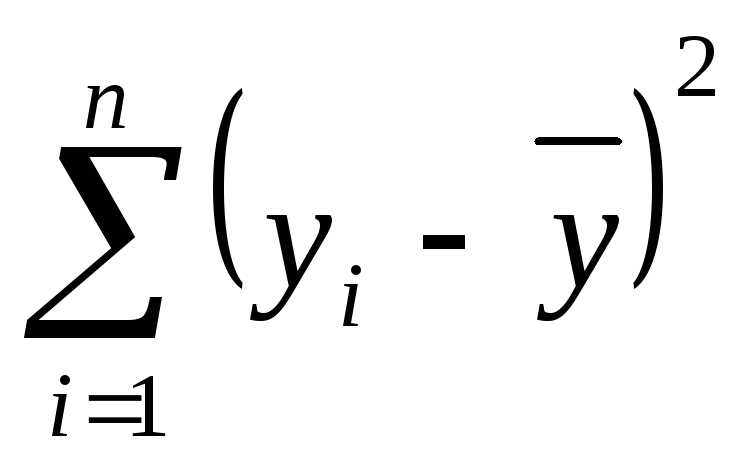на составляющие, обусловленные регрессией и неучтенными факторами. Коэффициент детерминации и корреляционное отношение.

49. Проверка значимости уравнения регрессии с помощью F-критерия Фишера-Снедекора.

50. Равномерный (прямоугольный) закон распределения и его числовые характеристики.

51. Понятие о функции распределения и плотности вероятности двумерной случайной величины.