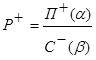решения задач

Вопрос №12. Обратные вычисления для реализации целевой установки

Целевая установка: у⁺ = f(x⁺⁽α), z⁺(β)).

Здесь и далее сумма КОВ всегда равна единице, т.е. α+β = 1.

Введем индивидуальные коэффициенты, с помощью которых определяются искомые приросты аргументов:

x+∆x=k1x,

z+∆z=k2z

Это позволяет записать задачу обратных вычислений в следующемвиде:

Поскольку y+∆y здесь уже рассматриваются в качестве аргумента, от которого зависят приросты ∆x и ∆z, следует определить диапазон исходных значений Ау, а и р , при которых задача имеет смысл.

Для этого следует решить систему неравенств вида:

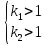
Пример. Известна зависимость прибыли П от выручки В и себестоимости продукции С, которую можно представить в виде П=В-С.

Целевая установка состоит в следующем: необходимо повысить прибыль за счет увеличения выручки и себестоимости, причем большая часть прироста прибыли должна произойти за счет увеличения выручки, а меньшая - за счет повышения себестоимости. Такая целевая установка представляется следующим образом:

П⁺ = В⁺(α) – С⁺(β), α 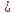β

Введем индивидуальные коэффициенты:

В+∆В=к₁В,

С+∆С=к₂С

Представим задачу обратных вычислений в виде системы уравнений:

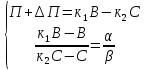
Решив ее относительно к₁ и к₂, получим:

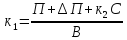
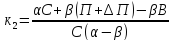
Вопрос 13. Обратные вычисления для реализации целевой установки

Y^f (x^(), z^()) на основе коэффициентов прироста аргументов

Введем индивидуальные коэффициенты:

Задача обратных вычислений:

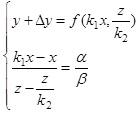
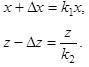
Пример.

Известна зависимость рентабельности (Р) от прибыли (П) и себестоимости продукции (С). Р=П/С Целевая установка следующая: повысить рентабельность за счет повышения прибыли и снижения себестоимости, причем большая часть прироста рентабельности должна произойти за счет повышения прибыли, а меньшая - за счет снижения себестоимости, что можно выразить следующим образом:

Р+ + П+ С -

Введем индивидуальные коэффициенты и составим систему уравнений:

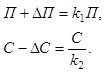
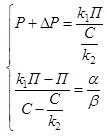
Решив ее, относительно К1и К2, получим: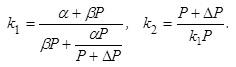

Проверка:

Вопрос 16. Целевая установка: у^- = f (x⁺(α),z⁺(β)).

Как и ранее, введем индивидуальные коэффициенты, с помощью которых определяются искомые приросты аргументов:

х + ∆х = k₁x

Z + ∆z =k₂Z

Это позволяет записать задачу обратных вычислений в следующем виде:

y-∆y = f(k₁x,k₂z),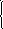

=

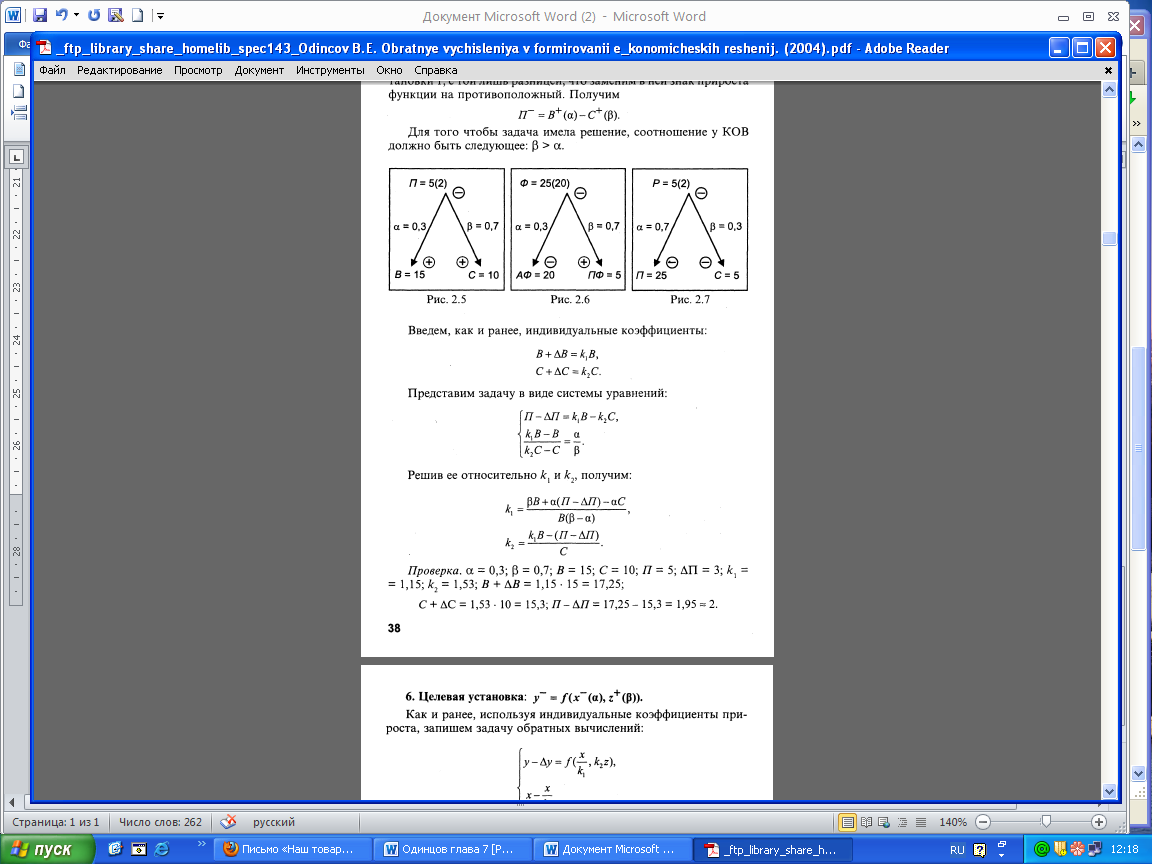
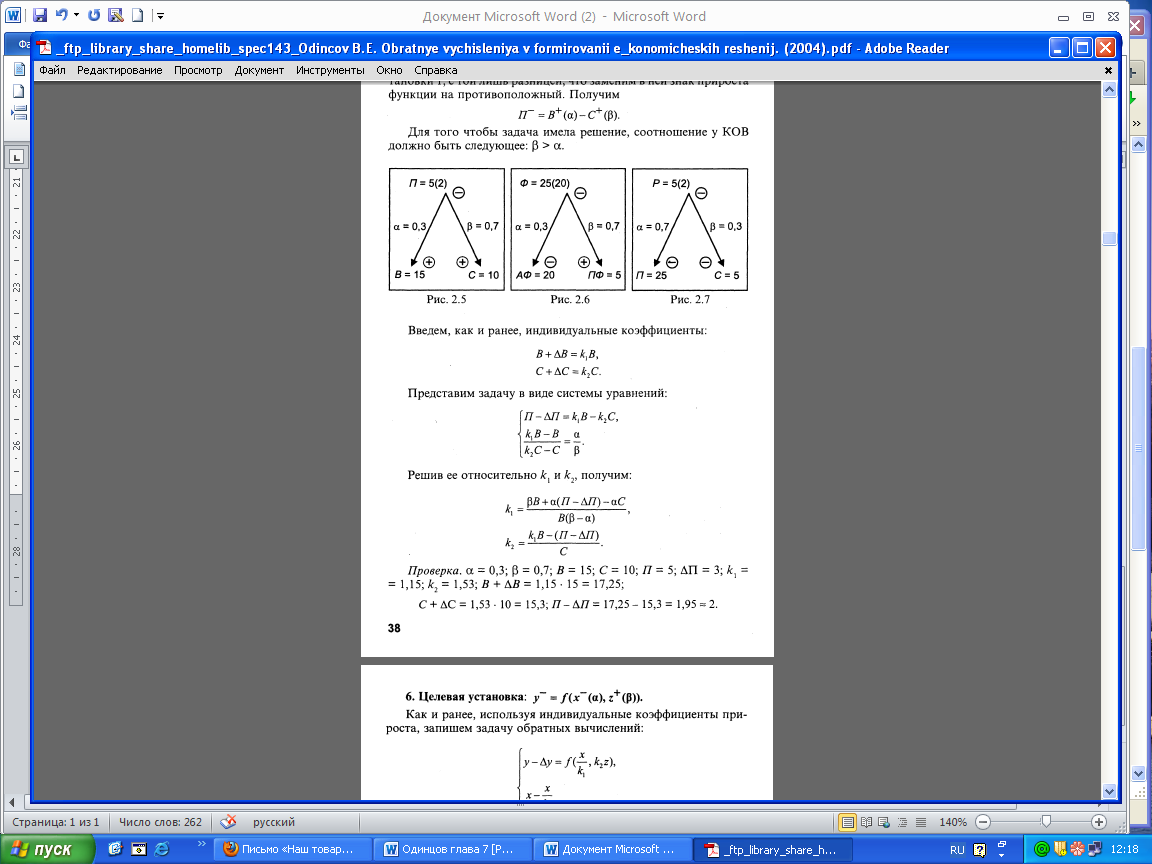
Пример (рис. 2.5). Воспользуемся примером из целевой установки 1, с той лишь разницей, что заменим в ней знак прироста функции на противоположный. Получим

П^- = B⁺(α)-C⁺(β)

Для того чтобы задача имела решение, соотношение у КОВ должно быть следующее: β > α.

Вопрос 18. Обратные вычисления для реализации целевой установки

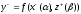на основе коэффициентов прироста аргументов

Запишем задачу обратных вычислений (два выражения под фигурной скобкой, числа это индексы):

У- Δу=f(x/k1, k2z)

(X-x/k1)/(k2z-z)= α /β

Воспользуемся исходными данными из целевой установки 3, однако изменим задачу в соответствии с целевой установкой 6. Будем считать, что объем производственных

фондов необходимо понизить за счет снижения А Ф, но одновременного повышения ПФ; изменения производить большей частью за счет ПФ. Согласно такой целевой установке получим:

Введем индивидуальные коэффициенты:

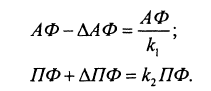
Составим систему уравнений:

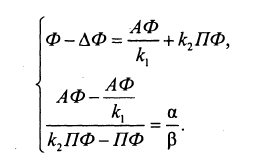
Решив её, получим:

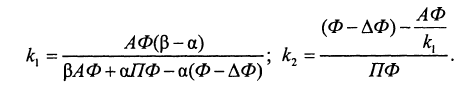
Вопрос 20. Обратные вычисления для реализации целевой установки

y+ = f (x+(a), z+(b )) на основе единого коэффициента прироста аргументов

Пусть, как и ранее, задана функция y=f(x, z). Введем величину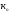 которая, будучи умноженной на КОВ каждого из аргументов, позволит получить желаемый для них прирост.

Целевая установка: у = f(x(a), z(ɮ)).

Введем единую величину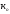 и получим искомые приросты следующим

образом:

∆х=a*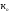 ∆z= ɮ *

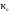
Задача обратных вычислений заключается в поиске величины 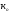из уравнения:

y+∆y=f(x+a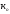, z+ ɮ)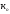

Пример (рис. 2.8). Умножением количества на цену получают выручку, приобретенную в результате реализации продукции. Формула расчета имеет вид:

P=К*Ц где Р - выручка; К - количество продукции; Ц - продажная цена.

Допустим, целевая установка следующая: нарастить выручку за счет увеличения количества продаваемой продукции и ее цены. При этом большая часть выручки должна быть получена за счет увеличения количества (а > ɮ ). Такая установка отразится следующим образом:

Р=К(а)*Ц( ɮ), а> ɮ.

Введем величину 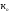и получим:

∆К=a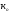;∆Ц= ɮ;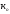

P+∆P= (K+a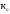)(Ц+ ɮ ) =

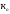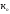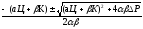
Вполне очевидным ограничением на исходные данные служит следующее неравенство:

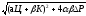> - (aЦ+ ɮК).

Проверка, а = 0,6; ɮ = 0,4; К = 12; Ц = 4; Р = 48; Р ∆= 12; к= 1,58; ∆К: = 0,6 • 1,58 = 0,95; ∆Ц = 0,4 • 1,58 = 0,63; К + ∆К = 12 + 0,95 = 12,95; Ц + ∆Ц = 4+ 0,63 = 4,63; Р + ∆Р = 12,95 • 4,63 = 59,958 = 60.

Вопрос 21. обратные вычисления для реализации целевой установки

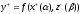на основе единого коэфициэнта прироста аргументов.

Это целевая установка прямой задачи. пример: Какова рентабельность пред - ия ?)

Следствие = f(причина)

Результат = f (затраты)

Достижение = f (средства)

сама функция, так и ее аргументы могут либо увеличиваться, либо уменьшаться. С помощью индивидуальных коэффициентов, если прирост положительный, то индивидуальный коэффициент должен умножаться на свой аргумент, если отрицательный, то - аргумент должен делиться на него.

Вводим индивидуальные коэффициенты:

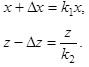
Обратные вычисление примет вид:

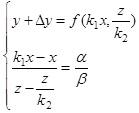
Пример:

Рентабельность зависит от П (прибыли) и С (себестоимости)

Целевая установка: повысить Р за счет повышения П и снижения С.

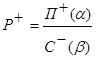 Вводим индивидуальные коэффициенты и составляем систему уравнений:

 

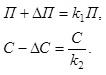
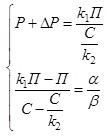
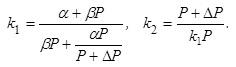
Проверка:

Вопрос 22. Обратные вычисления для реализации целевой установки

y+ = f (x-(a), z+(b )) на основе единого коэффициента прироста аргументов

Обратные вычисления — это получение точечных значений приростов аргументов прямой функции на основании ее задаваемого значения и дополнительной информации, поступающей от лица, формирующего решение. Точечными они называются потому, что отыскиваются новые значения аргументов лишь для указанных менеджером функций.

Дополнительная информация, используемая при этом, следующая:

целевая установка лица, формирующего решение, которая выражается с помощью знаков («плюс» — увеличение или «минус» — уменьшение) приростов каждого из аргументов прямой функции;

приоритетность в путях достижения целей, отражаемая с помощью коэффициентов (не обязательно).

Принцип выполнения обратных вычислений. Вид формул, обеспечивающих прямые вычисления, может быть сколь угодно разнообразным, поэтому методика выполнения обратных вычислений предполагает их приведение к стандартному виду.

Пример. Известна зависимость прибыли (П) от выручки (В) и себестоимости продукции (С), которую можно представить в виде формулы П = В-С.

Целевая установка состоит в следующем: необходимо повысить прибыль за счет повышения выручки и себестоимости, причем большая часть прироста прибыли должна произойти за счет повышения прибыли, а меньшая — за счет повышения себестоимости (рис 7.9):

П⁺ = В⁺(а) - С⁺(Р), а > р.

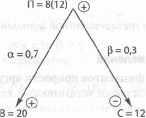
Рис. 7.9. Графическая иллюстрация целевой установки «Повысить прибыль»

Введем индивидуальные коэффициенты: В + ДВ = *,В, С + ДС = *₂С.

Представим обратную задачу в виде системы уравнений:

П + ДП = *,В-£₂С, < к_хВ-В ос к₂С-С~ р'

Решив ее относительно к_х и к₂, получим

П + ДП + к₂С В ' _ аС + Р(П + АП)~рВ ²~ С(а-Р)

Проверка: а = 0,7; р = 0,3; В = 20; С = 12; П = 8; ДП = 4; Л, = 1,35; к₂ = 1,25; В + ДВ = 1,35-20 = 27; С + ДС = 1,2512 = 15; П + ДП = 27 - 15 = 12.

Вопрос 24. Обратные вычисления для реализации целевой установка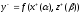без указания приоритетности целей.

Решение:

Y ^- = f (Х⁺; Z⁺ ), Y - ∆Y = f (Х*k; Z*k )

Пример. П = В – С (П- прибыль, В – выручка, С- рентабельность)

П ^-

α β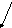

В⁺ С ⁺

П ^- =В⁺ - С ⁺

П - ∆П = В +∆В – (С+∆С)

В+∆В = В*k ; С+ ∆С = С*k

П - ∆П = В*k - С *k = k*(В - С)

k = (П - ∆П) / (В – С) = (П - ∆П) / П