
adambaev_avtomatty
.pdf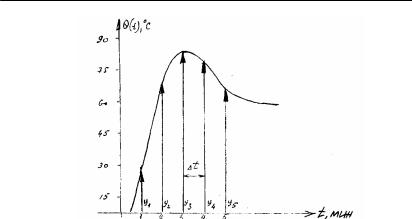
Автоматты басқару теориясы
2.4-сурет. Тербелiс екпiн ºисы¹ына ие екінші ретті объектінің теңдеуін анықтау
Екпiн ºисы¹ы тербелiс т¾рде болғандыºтан, iзделiп отыр¹ан те»деудi комплекстi т¾бiрлерге ие екiншi реттi те»деу деп алу¹а болады [13]:
d 2 Dq |
- (g |
|
+ g |
|
) × |
dq |
+ g |
|
×g |
|
× Dq = g |
|
×g |
|
× k ×u ; |
(2.49) |
|
dt 2 |
1 |
2 |
dt |
1 |
2 |
1 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
g 1 , g 2 , k т½раºтыларды есептеу ºажет. Б½л те»деу 2.2.2-
пункттегi те»деу сияºты. Тек ºана т½раºтыларды» белгiлеуi ¼згертiлген:
g1 |
= - |
1 |
,g 2 |
= - |
1 |
. |
|
|
|||||
|
|
T1 |
|
T2 |
||
Тербелiс ж¾йенi» те»деуi ¸детте мына т¾рде жазылады:
d 2 Dq |
+ 2 |
×e ×w0 |
× |
dDq |
+w |
2 |
× Dq = k ×w |
2 |
dt 2 |
dt |
0 |
0 |
|||||
|
|
|
|
|
|
|
×u; (2.50)
ì½íäàғы e - демпфинг (азайту) коэффициентi; w0 – æ¾éåíi» ¼çiíäiê æèiëiãi.
69

М.Д. Адамбаев, Т.С. Малдыбаева
(2.49) ж¸не (2.50) те»деулерден физикалыº e , w0
т½раºтыларымен g 1 , g 2 сандар арасында¹ы байланысты к¼ремiз.
g |
ìåí g |
2 |
есептеудi о»айлату ¾шiн енгiзiлген. |
||||
1 |
|
|
|
|
|
|
|
|
2.2.2 пункттегi н¸тиженi ºолданып, те»деудi» шешiмiн |
||||||
жазамыз: |
|
|
k × a ×g 2 |
|
k × a ×g1 |
|
|
|
|
|
Dq (t) = k ×a + |
×eg1×t + |
×eg 2 ×t . |
||
|
|
|
g1 -g 2 |
|
|||
|
|
|
|
|
g 2 -g1 |
||
Басºару объектiсi – тербелiс ºасиеттерге ие бол¹андыºтан, т½раºтыларды есептегенде наºты сан емес, комплекстi санды аламыз:
g 1 = a + jb ; |
g 2 = a - jb . |
(2.51) |
Эйлер формуласын ( e ± jj |
= cosj ± j sin j ) |
ºолданып, |
(2.51) шешiмдi келесi т¾рде жазамыз [13]:
Dq (t)
=k × a
=k × a
=k × a
= k × a ×[1 + |
a - jb |
× e(a + jb )×t + |
a + jb |
× e(a - jb )×t ] = |
|
|||||||||||||||||
|
|
|
|
|
|
|
2 jb |
|
|
|
|
|
|
- 2 jb |
|
|
|
|
|
|
||
|
ì |
|
at |
|
é ja + b |
|
|
|
|
|
|
|
|
|
|
|
ja - b |
ùü |
(2.52) |
|||
× |
í1 |
+ e |
|
× ê |
|
|
|
|
× (cos bt + |
j sin bt )+ |
|
|
× (cos bt - j sin bt )úý |
= |
||||||||
|
|
- 2b |
|
|
2b |
|||||||||||||||||
|
î |
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
ûþ |
|
|||
|
é |
+ eat |
|
æ |
|
|
|
|
|
|
|
a |
|
öù |
|
|
|
|
|
|
|
|
× |
1 |
× |
ç |
- cos bt + |
|
×sin bt ÷ |
= |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
ê |
|
|
|
ç |
|
|
|
|
|
|
|
b |
|
÷ú |
|
|
|
|
|
|
|
|
ë |
|
|
|
è |
|
|
|
|
|
|
|
|
øû |
|
|
|
|
|
|
|
|
|
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ù |
|
|
|
|
|
|
|
|
|
æ a |
ö |
2 |
|
|
æ |
|
|
b |
|
|
||||||
|
ê |
|
at |
|
|
|
|
|
|
|
|
öú |
|
|
||||||||
× |
+ e |
|
× |
|
1 + ç |
|
÷ ×sinç bt - arctg |
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
÷ . |
|
|
||||||||||||||
|
ê |
|
|
|
|
ç |
|
÷ |
|
|
|
è |
|
|
a øú |
|
|
|||||
|
|
|
|
|
|
è b |
ø |
|
|
|
|
|
|
|
||||||||
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
(2.52) те»деуi екi гармониканы» ºосындысына с¸йкес.
Åêïií |
ºèñû¹ûíàí |
áiðäåé |
Dt = 5мин |
аралыº |
|
ºàøûºòûºòà¹û àëòû |
ординатаны |
аламыз: |
Dq0 = 0,0 ; |
||
Dq1 = 29,3 ; |
Dq2 = 69,0 ; Dq3 |
= 84,3 ; Dq4 = 79,8 ; Dq5 = 71,1 . |
|||
Кубтыº (2.43) те»деудi» коэффициенттерiн табу ¾шiн те»деулер ж¾йесiн º½растырамыз:
0,0 × B3 + 29,3 × B2 + 69,0 × B1 + 84,3 = 0;
29,3 × B3 + 69,0 × B2 + 84,3 × B1 + 79,8 = 0;
69,0 × B3 + 84,3 × B2 + 79,8 × B1 + 71,1 = 0;
70

Автоматты басқару теориясы
Á½äàí: |
B = -1,654 ; B |
2 |
= -1,12 ; |
|
B = -0,366 |
ж¸не келесi |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
кубтыº те»деудi аламыз: |
|
|
|
|
|
|
|
|
|
|||||
|
|
l3 -1,654 × l2 |
|
+1,12 × l - 0,366 = 0. |
|
|||||||||
Оны» т¾бiрлерiн есептеймiз (бiр т¾бiрi алдын ала белгiлi |
||||||||||||||
l3 = 1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
= 0,327 + j × 0,509 ; |
|
l2 = 0,327 - j × 0,509 ; |
l3 = 1 . |
||||||||||
Комплекстiк |
l |
|
æ¸íå |
|
l |
2 |
т¾бiрлерiн к¼рсеткiштiк т¾рде |
|||||||
жазамыз: |
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
= e-0,5+ j×1,0 ; l |
2 |
= e -0,5- j×1,0 . |
|
|||||||
|
|
g |
1 |
g |
|
|
|
|
|
|
|
|
||
Содан кейiн |
1 |
, |
2 |
т½раºтыларды табамыз: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
g 1 = - 1
T1
g 2 = - 1
T2
=ln l1
Dt
=ln l2
Dt
= |
- 0,5 |
+ j ×1,0 |
= -0,1 + j × 0,2; |
ü |
|
||
|
|
|
|
ï |
|
||
|
|
5 |
|
(2.53) |
|||
|
|
|
|
|
ï |
||
|
|
- 0,5 - j ×1,0 |
|
ý |
|
||
= |
= -0,1 - j ×0,2ï |
|
|||||
|
|
||||||
|
|
|
5 |
|
|
ï |
|
|
|
|
|
|
þ |
|
|
(a = -0,1; b = 0,2) .
Ендi статикалыº k áåðiëiñ |
коэффициентiн есептеу |
ºажет. Оны, есептелген a ìåí b |
т½раºтыларын ж¸не екпiн |
ºисы¹ынан кез келген н¾ктенi» координаттарын алып диференциялды те»деудi» шешiмiне ºоя отырып, о»ай
есептеуге болады. Мысалы, |
t = Dt = 5мин , |
Dq (Dt) = Dq1 = 29,3 |
||||
координаттар¹а ие н¾ктенi аламыз: |
|
|
||||
|
é |
|
æ |
|
a |
öù |
Dq = k ×1× |
1 |
+ eat ×ç |
- cos bt + |
|
sin bt ÷ |
|
|
||||||
|
ê |
|
ç |
|
b |
÷ú |
|
ë |
|
è |
|
øû |
|
немесе: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29,3 = k ×1× |
é |
+ e |
-0,1×t |
æ |
|
|
|
- 0,1 |
|
öù |
. |
||||
1 |
|
|
×ç |
- cos 0,2 |
×5 |
+ |
|
|
×sin 0,2 |
×5÷ |
ú |
||||
|
|
|
|
||||||||||||
|
|
ê |
|
|
|
è |
|
|
|
0,2 |
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
øû |
|
|||
Á½äàí: k = 70 |
|
град |
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
м / са |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тербелiс объектiнi» iзделген сандыº те»деуi төмендегідей:
d 2 Dq |
+ 0,2 × |
dq |
+ 0,05 × Dq = 0,05 × 70 ×u |
(2.54) |
dt 2 |
dt |
|
71
М.Д. Адамбаев, Т.С. Малдыбаева
ì½íäà u = м / са ; Dq =0C;[t]= мин; . |
|
|||||||
Объектiнi» ¼зiндiк жиiлiгi: |
|
|
|
|||||
w0 = |
|
|
= 0,224 рад / мин; |
(2.55) |
||||
g 1 ×g 2 |
||||||||
Демпфингтеу коэффициентi: |
|
|||||||
e = |
- l1 - l2 |
|
= |
|
0,2 |
= 0,45 . |
(2.56) |
|
2 ×w0 |
|
× 0,234 |
||||||
|
2 |
|
|
|||||
Осы т¸сiлдi жо¹ары реттi ж¾йелер ¾шiн ºолдан¹ан кезде, ¸дiстi» жалпы схемасы ¼згермейдi.
2.2.4. Екпiн ºисы¹ы бойынша объектiнi» берiлiс функциясын аныºтау
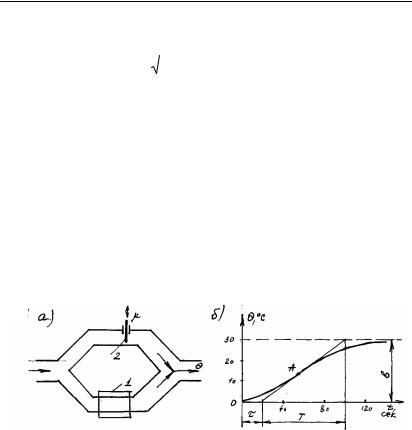
Б½л м¸селенi наºты объект ¾шiн ºарастырамыз. Мысалы, домна пешiне байытыл¹ан оттектi ¾рлеу (оттектi алдымен 1000-12000Ñ дейiн ºыздырады). ²ыздыруды» о»айлатыл¹ан с½лбасы 2.5à-суретте келтiрiлген.
2.5-сурет. а) пешке оттектi ºыздыру с½лбасы; ə) оттек ºыздыру кезiндегi екпiн ºисы¹ы
Ñóûº àóаны» а¹ыны екiге б¼лiнедi: бiр б¼лiгi ауа жылтºыштан (1) ¼тедi, екiншi б¼лiгi – реттегiштi» дросселi (2) арºылы ¼тедi. Содан соң екi б¼лiк, пешке берiлер алдында ºосылады, ал оларды» температуралары орта м¸нді. Á½ë q температураны т½раºтандыру ¾шiн, автоматты ж¾йенi» реттеушi б¼лiгiн дроссельдi (2) жылжытады. Сонымен, объектiнi» кiрiс шамасы дроссельдi» m жайы (к¾йi) болады,
ал шы¹ыс шамасы – ыстыº ауаның q температурасы болады. 2.5ə-суретте объектiнi» экспериментальäû åêïií ºèñû¹û
72

Автоматты басқару теориясы
êåëòiðiëãåí. Îë, êiðiñi Dm = 5% ¼згергенге с¸йкес. Объектiнi» сандыº берiлiс функциясын аныºтаймыз:
W (p )= q (p) .
m(p )
К¼п жа¹дайда т¸жiрибеде осындай екпiн ºисы¹ына ие объектiлердi кешiгуi бар инерциалы буынмен аппроксима- циялайды:
W (p )= |
q (p) |
|
= |
kоб |
|
×e |
-t × p . |
(2.57) |
m(p ) |
T × p +1 |
|
|
|||||
Егер д¸лдiктi ¹ана емес, сонымен ºатар ºарапайымдылыºты (о»айлыºты) ба¹аласаº, онда б½л аппроксимацияны е» ºолайлыларды» бiреуi деп есептеуге болады.
Åêïií ºèñû¹ûíû» å» ¾ëêåí èiëãåí æåðiíå (À н¾ктесi) жанама сызыº ж¾ргiзедi. Ол сызыº – уаºыт осi ж¸не асимптотамен ºиылысады (асимптота¹а екпiн ºисы¹ы
ба¹ыттал¹ан). Содан кейiн t , |
T æ¸íå kоб ¼лшейді (2.5ә- |
|||||||||||
сурет). |
Берiлген мысал |
¾øií |
t = 20 ñåê; |
T = 80 ñåê; |
||||||||
kоб = |
b |
= |
300 C |
= 6 0Ñ/%жүріс. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
Dm 5% жрi |
|
|
|
|
|
|
|||||
Берiлiс функция мына ò¾ðде болады: |
|
|
||||||||||
|
|
|
|
|
q (p) |
|
|
6 |
|
|
-20× p . |
(2.58) |
|
|
|
|
W (p )= m(p ) |
= 80 p +1 |
×e |
||||||
|
|
|
|
|
|
|||||||
ì½íäà [q ]=0 C ; [m]= %æүðiñ; [Т ]= сек .
Т½раºтыларды аныºтауды тездетіп, есептеу ж½мысыны» к¼лемiн азайтуға ºолданылатын т¾рлi графо-аналитикалыº ¸дiстер бар.
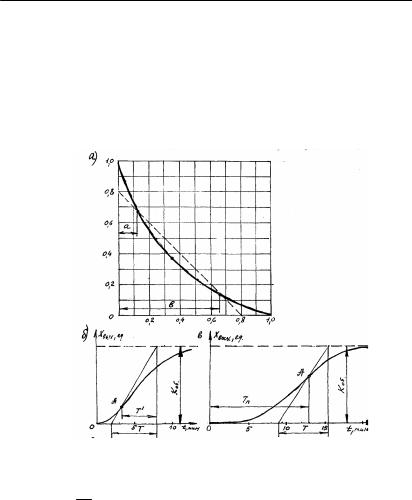
2.6à-суретте номограмма келтiрiлген. Б½л номограмма бойынша екi сыйымдылыºты объектiнi» екi уаºыт т½раºтыларын тез аныºтау¹а болады [14]. Îë ¾øií åêïií ºèñû¹ûíäà (2.6ə-сурет)
À н¾ктесi, содан соң T ' æ¸íå T алынады. Номограмманы» екi
осi бойымен T ' |
кесiндiсi ¼лшенедi. Ол кесiндiлердi» со»ы |
|
|
T |
|
òүзумен ºосылады. Түзудi» номограмма графигiмен ºиылысºан н¾ктелерiнi» координаттарын à æ¸íå á-деп белгiлеймiз. График симметриялы бол¹андыºтан, ºиылысу н¾ктелердi» ºайсысын
73
М.Д. Адамбаев, Т.С. Малдыбаева
àëñàºта б¸рiбiр. Содан соң iзделген уаºыт т½раºтыларын мына байланыстар арºылы табады:
T ' |
T1= a·T ; T2=в×T . |
(2.59) |
|
= 0,73 áîë¹àíäà, түзу сызыº номограмма |
ºèñû¹ûíà |
||
T |
|||
|
|
жанама ж¸не T1 = T2 = 0,365 ×T .
2.6-сурет. Номограмма бойынша екi сыйымдылыºты буынны» уаºыт т½раºтыларын аныºтау
Åãåð T ' á0,73 болса, онда т½зу сызыº номограмма
T
графигiмен ºиылыспайды. Б½л ж¾йе – бiрiншi реттi екi буынмен аппроксимацияланбайтынын бiлдiредi. Б½л
жа¹дайда, объектiнi T1 æ¸íå T2 уаºыт т½раºтылар¹а ие ж¸не t кешiгуi бар екi инерциалы буынмен аппроксимациялайды. Сонымен:
T1 = T2 = 0,365 ×T ; t = TП - 0,365 ×T . |
(2.60) |
74

Автоматты басқару теориясы
Ендi графоаналитикалыº ¸дiстi – объектiлердi» берiлiс функцияларын, оларды» екпiн ºисыºтары бойынша (2.6ə;2.6б-сурет), аныºтауға ºолдануды ºарастырайыº.
2.6 ə-суретi ¾шiн T = 6 ìèí, T ' = 4,8 ìèí, |
T ' |
= 0,8 -ãå òå». |
|
T |
|||
|
|
µзынды¹ы 0,8-ге те» кескiндi, номограмма осьтерi бойымен ¼лшеймiз (2.6а-сурет). Б½л кескiндердi» со»ын т¾зумен ºосамыз (штрих сызыº). ²иылысºан н¾ктелердi» координаттары a = 0,67 ;
b = 0,13. Аппроксимацияланып отыр¹ан буындарды» уаºыт т½раºтылары:T1 = T × a = 6 ×0,67 = 4,02 мин ; T2 = T ×в = 6 × 0,13 = 0,78 мин .
Объектiнi» берiлiс функциясы:
|
|
|
xшыг (р) |
|
|
коб |
|
|
|
|
|
|
|
|
коб |
||||||
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|
. |
||||||
|
|
|
х |
кiр |
(р ) |
(T × p +1)× (T × p +1) |
(4,02 × р +1)× (0,78 × р +1) |
||||||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Åêïií ºèñû¹ûíàí (2.6б-сурет) аламыз: T = 6,6 ìèí; TП =13 ìèí; |
|||||||||||||||||||
Т |
1 |
= T = 0,365×T = 0,365× 6,6 = 2,4 ìèí; t = T |
П |
- 0,365 ×T = 13 - 2,4 = 10,6 ìèí. |
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Объектiнi» берiлiс функциясы: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
шыг |
(р) |
к |
об |
×е- рt |
|
|
|
к |
об |
×е-10,6 р |
||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
, |
|
||||
|
|
|
|
|
|
хкiр (р ) |
(Т1 × р +1)× (Т 2 × р +1) |
(2,4 × р +1)2 |
|
||||||||||||
ì½íäà [t]= мин.
2.2.5. Екпiн ºисы¹ы бойынша объект те»деуiнi» ретiн аныºтау
Жо¹арыда ºарастырыл¹ан есептерде бiз, ж¾йенi» ба¹ытын суреттейтiн те»деудi» ретi белгiлi деп есептегенбiз. Ауыспалы функция бойынша те»деудi» ретiн д¸л аныºтау ¾шiн, келесi ереженi ескеремiз: егер ºисыºты» графигi n экспоненталарды» ºосындысы деп алынып, ол бiрдей ºашыºтыºты ординаталар¹а б¼лiнсе, онда оларды» ¸рºайсысы алдың¹û n ординаталардан т½ратын сызыºты комбинация болады. Басºаша айтºанда, ¸рбiр ордината алдың¹û n ординатадан т½раºты шкала¹а ие сызыºты рекуренттi ¼рнек бойынша алынады. М½ны» д¸лелдеуi – айырымдыº те»деу мен дифференциалдыº те»деудi эквиваленттеуден шы¹ады [7]. n -реттi объектiнi» екпiн ºисы¹ы
75

М.Д. Адамбаев, Т.С. Малдыбаева
n экспонента¹а ие. Б½л экспоненталарды бiлмей, олардың санын былай табу¹а болады. Екпiн ºисы¹ыны» графигiнен алдымен
т½раºтал¹ан º½растырушыны |
xc' т |
алып тастап, содан со» кез |
келген интервал аралыºпен |
x1 , |
x2 , … ординаталарды белгiлеу |
керек. Мысалы n ñàíû áåëãiëi болғанда:
хn+1 = xn+2 =
т.c.c.
A × x |
|
+ A × x |
|
+ ... + A × x , ü |
|
1 |
n |
2 |
n-1 |
n 1 ï |
(2.61) |
A1 × xn+1 + A2 × xn |
+ ... + An × xn ,ý |
||||
ï
þ
(2.61)-тi» кез келген n òå»äåói áåëãiсiз коэффициенттерге ие n сызыºты те»деулер ж¾йесiн º½райды. Б½л ж¾йенi» аныºтауышы н¼лге те» емес:
|
xn |
xn-1 |
... |
x1 |
|
|
|
|
|
|
Dn = |
xn+1 |
xn |
... |
x2 |
|
¹ 0 . |
|
(2.62) |
||
|
... |
... ... ... |
|
|
|
|
|
|||
|
x2n-1 |
x2n-2 |
... |
xn |
|
|
|
|
|
|
Åíäi òå»äåóäi» øûí ðåòi n -ãå òå» äåëiê те бiз ºателесiп, |
||||||||||
îíû ( n +1)-ге те» деп алайыº. |
|
|
|
|
|
|
|
|||
n +1 те»деудi» аныºтауышы: |
|
|
|
|
|
|
||||
|
|
xn+1 |
xn |
xn-1 |
|
... |
x1 |
|
|
|
|
|
|
|
|
||||||
Dn+1 = |
xn+2 |
xn+1 |
xn |
|
... |
x2 |
= 0 |
(2.63) |
||
... |
... |
... ... ... |
|
|||||||
|
|
|
||||||||
|
|
x2n+1 |
x2n |
x2n-1 ... |
xn+1 |
|
|
|||
н¼лге те», ¼йткенi оны» ба¹аналарыны» (тiк ºатарлар) арасында сызыºты байланыс бар: мысалы бiрiншi ба¹ана, (2.61) ¼рнек бойынша, басºаларды» сызыºты комбинациясы
арºылы алынады. ²ал¹ан Dn+2 , Dn+3 аныºтауыштарда, осы
себептен н¼лге те» болады. Алдың¹ы аныºтауыштар н¼лге те» болуы м¾мкiн емес.
Жо¹арыда айтыл¹андар, белгiзiз n санын аныºтау ¾шiн ºажеттi ереже (критерий) шы¹ады: екпiн ºисы¹ыны» бiрдей
76

Автоматты басқару теориясы
ºашыºтыºты ординаталары àðºûëû Di ( i = 1,2,3.... )
аныºтауыштар есептеледi. Е» бiрiншi болып, н¼лге те» болатын аныºтауыш n санын к¼рсетедi. n саны, аныºтауышты» ретiнен, бiр сан¹а аз болады.
2.3. Жиiлiктiк ¸дiстер бойынша объект те»деулерiн аныºтау
2.3.1. Объектiнi» берiлiс функциясын, оны» экспериментальды жиiлiктiк сипаттамаларынан табу
Экспериментальды жиiлiктiк сипаттамаларды, объектiнi» кiрiсiне гармоникалыº тербелiс X кiр (t ) = Aкiр ×sin wi t áåðó
арºылы алады. Гармоникалыº тербелiстер т¾рлi жиiлiктерде wi берiледi. Объектiнi» шы¹ысында, осы тербелiстерге жауап, т½раºтал¹ан тербелiстердi X шыг (t)= Aшыг ×sin(wi t +j) тiркейдi.
|
Эксперимент н¸тижесiнде |
объектiнi» амплитудалы |
||
A(wi |
)= |
Aшыг (wш ) |
ж¸не фазалы |
жиiлiктiк сипаттамаларын |
|
|
Aкiр (wi ) |
|
|
аныºтайды [15].
Жиiлiктiк сипаттамалар – реттеу ж¾йелерiнi» анализi мен синтезi ¾шiн ке» ºолданылып, олар объект те»деулерiн табу¹а да м¾мкiндiк бередi. Енді соларды» бiреуiн ºарастыралûº.
Технологиялыº аºпараттар тiзбегiнi» берiлiс функциясын аныºтау ¾шiн, эксперимент арºылы тiзбектi» амплитудалы A(wi ) ж¸не фазалы j(wi ) жиiлiктiк сипаттамаларын табамыз.
2.4-кесте
wi , ðàä/ñåê |
0,2 |
0,5 |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
ò.ñ.ñ. |
|
|
|
|
|
|
|
|
|
|
||
P(wi ) |
0,45 |
0,261 |
0,1 |
0,37 |
0,5 |
0,47 |
0,39 |
0,317 |
ò.ñ.ñ. |
|
0,5 |
0,5 |
0,0 |
1,6 |
0,0 |
0,7 |
0,2 |
0,5 |
|||
ºàòåëiê, % |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
Q(wi ) |
-0,136 |
-0,2 |
0,0 |
0,17 |
0,0 |
- |
-0,224 |
-0,256 |
|
|
|
|
|
|
|
0,15 |
|
|
ò.ñ.ñ. |
||
ºàòåëiê, % |
0,5 |
0,5 |
0,0 |
1,7 |
0,0 |
|
0,6 |
0,5 |
|
|
|
|
|
|
|
1,3 |
|
|
|
77

М.Д. Адамбаев, Т.С. Малдыбаева
Объектiнi» кiрiс шамасы - X 0 (t), ал шы¹ыс шамасы - X (t). Эксперименттi» н¸тижесi 2.4-кестеде келтiрiлген. Кестеде A(wi ), j(wi ) емес, ал формулалар бойынша есептелген наºты P(wi ) ж¸не жорамал Q(wi ) жиiлiктiк сипаттамалар
áåðiëãåí: |
|
|
|
|
|
P(wi |
) = A(wi |
)× cosj(wi |
); |
(2.64) |
|
Q(wi |
)= A(wi |
)×sin j(wi |
.) |
||
|
Осы берiлгендер бойынша, объектiнi» берiлiс функциясын есептеу керек. Зерттелiп отыр¹ан технологиялыº тiзбекті ¾шiншi реттi динамикалыº ж¾йе деп есептеймiз. Б½л жа¹дайда, ¾шiншi реттi ж¾йенi» берiлiс функциясы мынадай:
|
|
|
|
|
X (p) |
|
|
|
b1 × p 2 + b2 × p + b3 |
|
. |
(2.65) |
|||||||||
|
|
W (p )= X |
0 |
(p )= p3 + a × p 2 |
+ a |
2 |
× p + a |
3 |
|||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
Åñåï a1 , a2 , a3 , b1 , |
b2 , b3 |
коэффициентерiн аныºтауда |
|||||||||||||||||||
жатыр. p ® jw |
ауыстырып, W (p)-íû |
|
P(w) |
|
æ¸íå Q(w)-¹à |
||||||||||||||||
т¾рлендiремiз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W (jw )= |
- b ×w 2 |
+ jb ×w |
+ b |
|
= P(w )+ jQ(w ). |
(2.66) |
|||||||||||||||
|
1 |
|
|
|
2 |
|
|
3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
- jw |
3 - a |
×w 2 + ja |
2 |
×w + a |
3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Îäàí: |
|
|
= (- j ×w3 - a1 ×w2 + ja2 ×w + a3 )×[P(w )+ jQ(w)]. (2.67) |
||||||||||||||||||
- b1 ×w 2 + jb2 ×w + b3 |
|||||||||||||||||||||
Б½л те»дiктi екiге б¼луге болады: |
|
|
|
|
|
= Q(w)×w3 . |
|
||||||||||||||
-w2 ×b + b + P(w)×w |
2 × a + Q(w)×w ×a |
2 |
- P(w)× a |
3 |
(2.68) |
||||||||||||||||
1 |
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
w × b2 + Q(w)×w2 × a1 - P(w)×w × a2 - Q(w)× a3 |
= -P(w)×w3 . |
(2.69) |
|||||||||||||||||||
Б½л те»дiктер жиiлiктi» барлыº м¸ндерiне ¸дiлеттi |
|||||||||||||||||||||
болады. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4-кестеден |
|
||||
(2.69) òå»äiãiíå |
|
сандыº |
м¸ндердi |
|
ºîÿ |
||||||||||||||||
отырып, те»деулер ж¾йесiн аламыз (wi =1,0; 2,0; 3,0; 4,0;):
1,0 × b2 + 0,0 × a1 - 0,1×1,0 × a2 + 0,0 |
× a3 |
= -0,1×1,0 |
× |
|
ü |
. (2.70) |
||||||||||||||||||||
2,0 |
× |
b2 |
+ |
0,17 |
× |
4,0 |
× |
a1 |
- |
0,37 |
× |
2,0 |
× |
a2 |
- |
0,17 |
× |
a3 |
= - |
8,0 |
ï |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
0,37 |
|
ï |
|
|||||||||||
3,0 × b2 + 0,0 × a1 - 0,5 × 3,0 × a2 + 0,0 × a3 |
= -0,5 × 27,0 |
|
|
ý |
|
|||||||||||||||||||||
|
|
ï |
|
|||||||||||||||||||||||
4,0 |
×b |
- 0,15 ×16,0 × a |
|
- 0,47 |
× 4,0 |
× a |
2 |
+ 0,15 |
× a |
|
= -0,47 |
× 64,8ï |
|
|||||||||||||
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
þ |
|
|||
78
