
adambaev_avtomatty
.pdf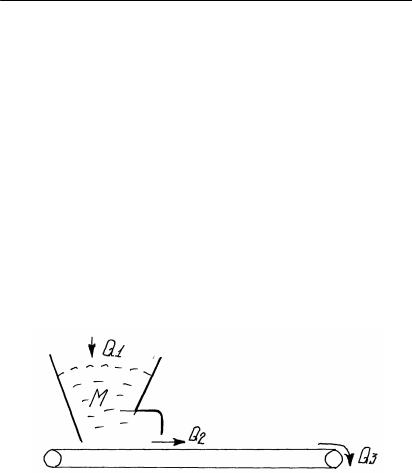
Автоматты басқару теориясы
dM1 (t ) |
|
= Q1 (t )- Q2' (t ); |
|
|
|
|
|
||
|
dt |
|
||
|
dM 2 (t ) |
= Q2' (t -t )- Q3 (t ). |
(1.5) |
|
|
|
|||
|
dt |
|
||
Мысал. Бункер-конвейер ж¾йесiнi» те»деуiн сандыº т¾рде º½ру (1.3-сурет). Егер бункердi» босатылуын ж¾зеге асыратын
конвейердi» |
½зынды¹ы |
l = 50 |
|
ì, ал лентаны» жылдамды¹ы |
|||||||
J = 1 ì/ñ = = 3600 ì/ñ๠|
болса, Q1 |
à¹ûí =100 ò/ñ๠= const . |
|||||||||
Øåøiìi. |
Бункер те»деуi: |
|
|
|
|
|
|||||
|
|
|
dM |
= 100 - Q2 (t ). |
|
|
|
||||
|
|
|
|
|
|
|
|||||
Конвейер те»деуi: |
|
dt |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
æ |
|
50 |
ö |
|
æ |
50 |
ö |
||
Q3 (t )= Q2 |
(t -t )= Q2 |
çt - |
|
|
÷ |
немесе |
Q2 (t )= Q3 çt + |
|
÷ . |
||
3600 |
3600 |
||||||||||
|
|
è |
|
ø |
|
è |
ø |
||||
1.3-сурет. Бункер-ковейер ж¾йесiнi» динамикасын аныºтау
Q2 аралыº шаманы шы¹арып тастап, iзделетiн те»деудi аламыз:
dM |
|
|
æ |
50 |
ö |
; |
|
|
=100 |
- Q |
çt + |
|
÷ |
||
dt |
3600 |
||||||
|
3 |
è |
ø |
|
ì½íäà¹û [M ]= m ; [Q]=т/сағ; [t]=сағ.
9

М.Д. Адамбаев, Т.С. Малдыбаева
Жо¹арыда ºарастырыл¹ан жа¹дайлар ºарапайым болғанымен, шын м¸нiнде барлы¹ы да к¾рделi болып келедi. Мысалы, жинаºты» ж½мыс процесi кезiнде (1.1-сурет) шамалар, ¼здерiнi» орташа м¸ндерiне, салыстырмалы аз ¼сiмше алады: DQ1 = Q1 - Qорт ; DQ2 = Q2 - Qорт ; DM = M - M орт ж¸не б½л кезде шы¹арылатын материалды» ¼сiмшелерi ерiксiз емес, олар ºор ¼сiмшесiне т¸уелдi:
DQ2 = к × DM ; |
(1.6) |
ì½íäà¹û ê - пропорционалдыº коэффициент. Басºа с¼збен
айтºанда, ºор ¼сiмшесi к¼п бол¹ан сайын, шы¹арылатын а¹ынны» жауапты ¼сiмшесi к¼п болады, я¹ни объект - сызыºтыº ¼зiн-¼зi т¾зеу эффектiсіне èå.
Кiрiс шамасы DQ1 , шы¹ыс шамасы DM болатын ж¸не кiрiс шамасы DQ1 , ал шы¹ыс шамасы DQ2 болатын жа¹дай
¾øií, æèíຠòå»äåóií º½ðàмыз. Åêi æà¹äàé ¾øií äå, óàºûò ò½ðàºòûëû¹û мен берiлiс коэффициентiн аныºтау керек.
Сызыºтыº ¼зiн-¼зi т¾зейтiн объектiлер ¾шiн ¼сiмшелер, шаманы» абсолюттi м¸нi сияºты, балланс те»деуiмен байланысты:
dDM = DQ1 - DQ2 . dt
Бiрiншi жа¹дайда, материалды баланс те»деуiнен DQ2 -íi
алып тастау керек. (1.6)-ны есепке ала отырып, мынаны аламыз:
dDM |
= DQ |
- к × DM |
немесе |
dDM |
+ к × M = DQ ; |
dt |
1 |
|
|
dt |
1 |
|
|
|
|
ì½íäàғы ê ñàíû - ¼зiн-¼зi т¾зеу коэффициентi деп аталады да,
те»деулер мына т¾рде жазылады:
1 |
× |
dDM |
+ DM = |
1 |
DQ ; |
(1.7) |
к dt |
к |
1 |
|
|||
|
|
|||||
10

Автоматты басқару теориясы
dDM |
туындысыны» |
алдында |
т½ратын |
1 |
= T |
|
|
к |
|||||
dt |
||||||
|
|
|
|
коэффициентi, уаºыт ¼лшемдiлiгiне ие ж¸не жинаºты» уаºыт т½раºтылы¹ы болаäû. Ñûçûºòûº æèíຠ¾øií DQ2 = к × DM ºатынасы, ¼сiмше ¾шiн ¹ана ¸дiл емес, сонымен ºатар: Q2 = к × M шамасыны» абсолюттi м¸нi ¾шiн де ¸дiл, осыдан:
T = |
1 |
|
M é |
т |
ù |
|
|
|
= |
|
ê |
|
= са ú . |
(1.8) |
|
к |
|
т / са |
|||||
|
|
Q2 ë |
û |
|
|||
Сызыºтыº жинаºты» уаºыт т½раºтылы¹ы, онда¹ы материал ºорыны» шы¹атын а¹ынына деген ºатынасына те».
Кiрiс шамасыны» DQ -ы» алдында т½ратын |
1 |
= кП |
|
к |
|||
|
|
коэффициентi, берiлiс коэффициентi болып табылады. Осы жа¹дай ¾шiн ол, Ò-¹а те» болып шыºты.
Балланс те»деуiне, екiншi жа¹дайы ¾шiн, |
DM шамасын |
||||||||||
алып тастау керек: |
|
|
dDQ2 |
|
|
|
|
|
|
|
|
|
1 |
× |
+ DQ |
2 |
= DQ ; |
|
(1.9) |
||||
|
|
|
|
||||||||
|
к dt |
|
|
1 |
|
|
|||||
|
|
|
|
M cp |
|
|
|||||
б½л жерде уаºыт т½раºтылы¹ы T = |
1 |
= |
òå», áiðຠáåðiëiñ |
||||||||
к |
Qcp |
||||||||||
|
|
|
|
|
|
|
|
|
|||
коэффициентi 1-ге те» екенiн к¼руге болады.
Енді қ½рамында айнымалыларды» сызыºтыº емес функциялары немесе уаºытаралыº туындылары бар сызыºтыº емес те»деулерге ие жинаºтар¹а келейiк.
Мысалы, кiрiсiн - Q1 à¹ûíû, øû¹ûñûí - Ì ºоры немесе
Q2 а¹ыны деп санап, а¹у резервуарыны» те»деуiн º½рамыз. Резервуар схемасы, жинаº схемасына (1.1-сурет) ½ºсас.
Материал балансы мынаны бередi: dM = Q1 - Q2 . ÁiðຠQ2 dt
т¸уелсiз айнымалы бола алмайды, ол Ì функциясы.
Гидромеханикадан |
белгiлi, са»ылаудан шыººан а¹ын |
||
Q2 = m ×w × |
|
|
за»дылы¹ына ба¹ынады, м½ндағы m - øû¹ûí |
2qH |
|||
11

М.Д. Адамбаев, Т.С. Малдыбаева
коэффициентi; w -салма ºимасыны» ауданы; g – еркiн º½лау ¾деуi; Í- резервуарда¹ы де»гей.
Резервуарда¹ы |
äå»ãåé |
ºîð¹à |
|
пропорционал: H = к12 × M |
|||||||||||||||||||
åêåíií åñêåрсек, |
Q2 |
= к1 × к2 |
|
|
, |
|
|
|
|
|
к2 = m ×w × |
|
|
. |
|||||||||
|
M |
|
|
ì½íäà |
|
2g |
|||||||||||||||||
Бастапºы те»деуге Q2 -нi ºойып, мынаны аламыз: |
|
|
|
||||||||||||||||||||
|
|
|
dM |
|
+ к |
× к |
|
|
|
|
|
|
= Q |
|
|
|
|
|
|||||
|
|
|
2 |
|
|
M |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
dt |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
резервуарды» сызыºтыº емес те»деуi. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
æ |
|
1 |
ö2 |
2 |
|
|
|
|
||||
Егер бастапºы |
те»деуге |
|
|
|
ç |
|
|
÷ |
ºîéñàº, |
îíäà |
|||||||||||||
|
|
|
|
|
|
|
|
M |
|
= ç к к |
÷ |
×Q2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
è |
|
1 |
2 ø |
|
|
|
|
|
||||
екiншi iзделетiн те»деу шы¹ады: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
æ |
|
|
1 |
|
ö2 |
|
|
|
|
dQ2 |
|
|
|
|
|
; |
|
|
|
|||
2 ×ç |
|
|
|
|
÷ ×Q × |
+ |
Q |
= Q |
|
|
|
||||||||||||
|
|
× к |
|
|
|
|
|
|
|||||||||||||||
|
ç к |
2 |
÷ |
2 |
|
|
dt |
|
|
2 |
1 |
|
|
|
|||||||||
|
è |
|
1 |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
á½ë äà ñûçûºòûº åìåñ òå»äåó.
Егер салманы» формасы (мысалы, цилиндрлiк), оны» ауданы (w = 1 ñì2) ж¸не резервуар ºимасыны» ауданы ( S =1 ì2 ) белгiлi болса, онда а¹ын резервуарыны» те»деуiн сандыº т¾рде алу¹а болады. Шешiмi, ê1 æ¸íå ê2 константаларыны» сандыº м¸нiн аныºтау¹а келтiрiледi. Цилиндрлiк салма арºылы суды» а¹уы кезiнде шы¹ын коэффициентi m = 0,82. Сондыºтан:
|
ê2=0,82·1ñì2· |
|
2 ×981см / с 2 »35,5 ñì2,5/ñ |
||||||||
æ¸íå [Н ] |
= ñì, |
îíäà |
[Q]=ñì3/ñ. Осыдан, Í= k 2 |
× M æ¸íå |
|||||||
Ì=S·H=1·104 ñì2·Í |
|
|
|
1 |
|
||||||
мынаны аламыз: |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к = |
|
1 |
|
= |
|
1 |
=0,01 ñì-1; |
|
|
|
|
1 |
|
S |
1×104 |
|
|
|
|||
|
[M ]= ñì3. |
|
|
|
|
||||||
ì½íäà¹û |
|
|
|
|
|
|
|
|
|
||
12
Автоматты басқару теориясы
Резервуарды» жалпы те»деуiне ê1 æ¸íå ê2 сандыº м¸ндерiн ºойып, берiлген жеке резервуар ¾шiн мынаны табамыз:
dM |
|
|
|
æ |
1 |
ö2 |
|
dQ |
|
= Q . |
|
+ 0,357 M = Q ; |
×Q × |
+ Q |
|||||||||
|
2 ×ç |
|
÷ |
2 |
|||||||
|
|
|
|||||||||
dt |
1 |
è 0,357 |
ø |
2 |
dt |
2 |
1 |
||||
|
|
|
|
|
|
||||||
Егер резервуардан с½йыºты итеретiн ауыртпалыº күшiне ºосымша герметикалыº резервуарда¹ы Ð сыртºы ºысымды
есепке алса не ¼згередi? |
|
|
|
|||
Б½л жа¹дайда Q2 = m ×w × |
|
орнына, бастапºы ºатынас |
||||
2gH |
||||||
|
|
|
|
|
|
|
Q2 (t )= m ×w × 2gH + |
2Pg |
áîëады, |
ì½íäàғы r - ñ½éûºòûºòû» |
|||
r |
||||||
|
|
|
||||
òû¹ûçäû¹û.
Радикал астынан сыртºы P ºысымының негiзделген жа»а мүшеci пайда болады. Герметикалыº резервуар ¾шiн есептеу, жо¹арыда ºарастырыл¹ан ашыº резервуар ¾шiн жасал¹ан есептеуге ½ºсас болады.
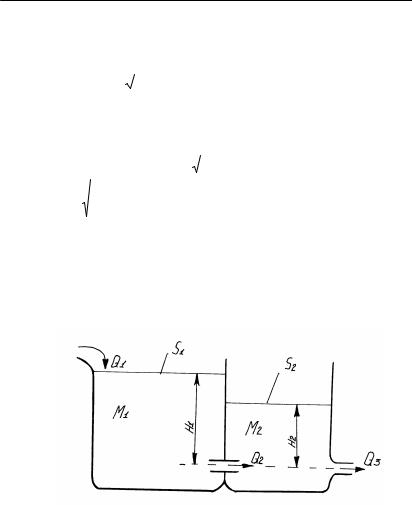
Төменде екi резервуардан º½рал¹ан каскадты» те»деуiн жазамыз (1.4-сурет).
1.4-сурет. Резервуарларды» каскады
Б½л жа¹дайда баланстыº ºатынастармен ºатар:
dM1 |
= Q - Q ; |
(1.10) |
|
dt |
1 |
2 |
|
|
|
|
|
13
М.Д. Адамбаев, Т.С. Малдыбаева
dM |
2 |
= Q |
2 |
- Q . |
(1.11) |
dt |
|
|
3 |
|
|
|
|
|
|
|
Мұнда келесi ºосымша т¸уелдiктер де орын алады:
Q3 = m1 ×w1 2gH 2 = k1 × |
H 2 ; |
(1.12) |
||||
Q2 = m2 ×w2 |
|
= k1' × |
|
; |
(1.13) |
|
2g(H1 - H 2 ) |
H1 - H 2 |
|||||
M 1 |
= r × S1 × H1 ; |
|
|
(1.14) |
||
M 2 |
= r × S2 × H 2 . |
|
|
(1.15) |
||
ì½íäàғы Ì1 æ¸íå Ì2 - ºорлар; Q1, Q2, Q3 - а¹ындар; S1 æ¸íå S2 – резервуар ºимасыны» ауданы; w1 , w2 - а¹ын са»ылаулары ºимасыны» ауданы; m 1, m 2 - шы¹ын коэффициенттерi; Í1, Í2 - материал де»гейлерi; r - материал ты¹ызды¹ы.
Шын м¸нiнде, жазыл¹ан те»дiктер каскадты» жиынтыº те»деулерi болып табылады. Бiраº кей жа¹дайда, кез келген айнымалылар арасында¹ы т¸уелдiлiктi табу ºажеттiлiгi туатындықтан, басºа айнымалыларды шы¹ару ºажет. Q3 øû¹ûñ æ¸íå Q1 кiрiс арасында¹ы т¸уелдiлiктi табу ºажет делiк. Ол ¾шiн Q2, Ì1, Ì2, Í1, Í2 айнымалыларын алып тастап, жиынтыº те»деулерде Q1 æ¸íå Q3 ºалдыру керек.
(1.12) ж¸не (1.15) те»деулерiнен мынаны аламыз:
|
|
|
|
|
æ |
|
ö2 |
|
|
|
|
||||
|
|
|
|
|
ç |
Q3 |
÷ |
; |
|
|
|
(1.16) |
|||
|
M 2 = r × S2 ×ç |
k |
÷ |
|
|
|
|
|
|||||||
|
|
|
|
|
è |
1 |
ø |
|
|
|
|
|
|||
онда (1.13) ж¸не (1.15), (1.16) те»деулерiнен: |
|
||||||||||||||
|
|
é |
|
|
ö |
2 |
|
æ Q |
ö |
2 |
ù |
|
|||
|
|
æ Q |
2 |
|
|
|
ú . |
(1.17) |
|||||||
M1 |
= r × S1 × |
êç |
|
÷ |
|
+ |
ç |
|
3 |
÷ |
|
||||
|
|
|
|
|
|
||||||||||
ç |
|
' ÷ |
|
ç |
|
k1 |
÷ |
|
ú |
|
|||||
|
|
êè |
k1 |
ø |
|
|
è |
|
ø |
|
|
||||
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
û |
|
14
Автоматты басқару теориясы
Ал (1.16) есепке ала отырып, (1.11) те»деуiнен:
é |
|
æ Q |
ö2 ù |
|
|
|
||
d êr × S |
2 × |
ç |
3 |
÷ |
ú |
|
|
|
ç |
k1 |
÷ |
|
|
|
|||
ê |
|
è |
ø |
ú |
|
|
|
|
ë |
|
|
|
|
û |
= Q |
2 |
- Q |
|
|
|
|
|
|
|||
|
dt |
|
|
|
|
3 |
||
|
|
|
|
|
|
|
||
немесе Q |
|
= Q |
|
+ |
r × S2 |
× 2Q |
|
dQ3 |
. (1.18) |
|
2 |
|
3 |
|
k12 |
|
3 dt |
||
(1.10) те»деуге (1.17) ж¸не (1.18) те»деулерiндегi Ì1 æ¸íå Q2 ì¸íäåðií ºояìûç:
d |
ì |
|
|
é |
1 |
æ |
|
|
ï |
|
|
|
|
|
|||
|
í |
r × S |
1 |
× ê |
|
çQ |
3 |
+ |
|
'2 |
|||||||
|
|
|
ç |
|
||||
dt ï |
|
|
êk1 |
è |
|
|
||
|
î |
|
|
ë |
|
|
|
|
r × S 2 |
|
|
dQ3 |
ö |
2 |
1 |
|
|
ùü |
|
|
|
|
|
2 |
ï |
|
||||
|
× 2Q |
3 |
|
÷ |
+ |
|
×Q |
|
úý |
+ |
2 |
|
2 |
|
|||||||
k1 |
|
|
dt |
ø |
|
k1 |
|
|
úï |
|
|
|
|
|
|
|
|
|
|
ûþ |
|
r × S 2 × 2 ×Q3 dQ3 + Q3 = Q1 . k12 dt
Á½ë åêiíøi ðåòòi ñûçûºòûº åìåñ òå»äåó, Q1 æ¸íå Q2 – уаºыт функциялары; ºал¹андары – константалар. Те»деу ретi - каскадта¹ы жинаºтар санына те».
1.1.2. Материалды а¹ындарды араластыру динамикасы
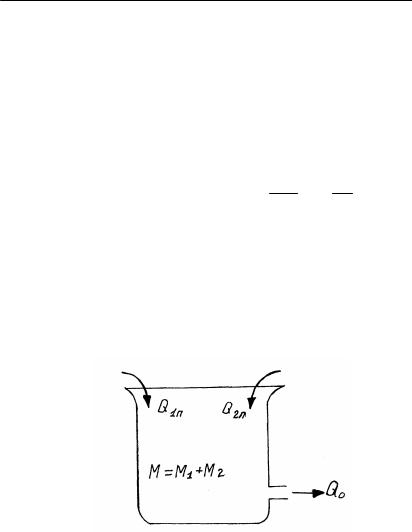
Төменде деалдыи араластыратын араластыр¹ышты» те»деуiн º½рамыз (1.5-сурет).
1.5-сурет. Араластыру динамикасы
Араластыр¹ышºа ¸р т¾рлi материалдарды» екi а¹ыны келiп түседi. Келтiрiлетiн материалдарды» шы¹ыны Q1Ï æ¸íå Q2Ï. Òîëûº êåëòiðiëåòií à¹ûí ò½ðàºòû:
QП = Q1П + Q2 П = const .
15

М.Д. Адамбаев, Т.С. Малдыбаева
Араластыр¹ышта¹ы материал ºорда т½раºты: M = M1 + M 2 . Æèíàºòàí ¸êåòiëåòií à¹ûí ìûíà¹àí òå»: Q0 = Q10 + Q10 . Êiðiñ
шамасы деп - Q1Ï , ал шы¹ыс шамасы деп - ¸кетiлетiн а¹ымда¹ы бiрiншi материалды» c1 концентрациясын санаймыз.
Берiлген мысалды екi ¸дiспен шешуге болады.
Áiðiíøi ¸äiñ. Идеалды аластыру кезiнде жинаººа келтiрiлетiн материал, жинаºта¹ы бар материалмен тез арада араласады. Сондыºтан, араластыр¹ыш к¼лемiнiнi» кез келген б¼лiгiнде ºарастырыл¹ан уаºытта, кез келген материалды» концентрациясы бiр болады. Бiрiншi материал ¾шiн материалдарды»
концентрациясын с1' (t ) деп белгiлейiк. °кетiлетiн а¹ында¹ы материал концентрациясы да сондай м¸нге ие екендiгiн к¼руге
болады, я¹ни c (t ) = c' |
(t ). |
|
|
||
1 |
1 |
|
|
|
|
Бiрiншi материал бойынша материалды балланс: |
|||||
|
|
|
dM1 |
= Q |
- Q . |
|
|
|
|
||
|
|
|
dt |
1П |
10 |
|
|
|
|
|
|
Îñû òå»äiêòi ìûíà ò¾ðгå ê¼øiðåìiç:
|
|
|
|
|
|
|
|
|
|
æ |
M |
1 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
M |
|
|
d ç |
|
|
÷ |
|
|
Q1П |
|
Q10 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
× |
è |
|
ø |
= |
- |
; |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
Q |
|
Q |
|
|
|
|||||||
орташа ал¹анда |
QП = Q0 |
|
= Q = const деп аламыз. |
|
|||||||||||||||||||||||
|
M |
1 |
= c' |
(t )= c (t ) |
æ¸íå |
|
|
|
Q1 |
= c |
(t ) |
áîë¹àíäûºòàí, |
|||||||||||||||
|
|
|
|
0 |
|||||||||||||||||||||||
|
M |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Q |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
M |
= |
dc1 (t ) |
+ c |
(t )= |
Q1П |
|
= c |
|
(t ), |
(1.19) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Q |
dt |
|
|
|
1 |
|
|
|
Q |
|
|
1П |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ì½íäàғы ñ1Ï – êåëòiðiëåòií QÏ а¹ында¹ы бiрiншi компоненттi» концентрациясы. (1.19) те»деу, iзделетiн те»деу болып табылады.
T = M шамасы араластыр¹ышты» уаºыт т½раºтылы¹ы, ал
Q
k = 1 - араластыр¹ышты» берiлiс коэффициентi. Егер кiрiс
Q
шамасы ñ1Ï äåï àëñàº, îíäà ê=1.
16

Автоматты басқару теориясы
Åêiíøi ¸äiñ. Б½л ¸дiс ыºтималдылыº теориясын ºолданумен негiзделедi [6]. m шары бар урнадан n шарды
(ºайтарумен) ал¹аннан кейiн, урнаны» iшiнде бiраз шар ºалу ыºтималдылы¹ы:
|
|
|
æ |
|
m |
ön |
|
|||||
|
|
P = ç |
|
|
|
|
|
÷ . |
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
n |
è m +1 |
ø |
|
|
||||||
Dt уаºыт интервалы кезiнде араластыр¹ышºа келiп |
||||||||||||
ò¾ñåòií |
áiðiíøi |
материалды» |
|
|
|
|
ñàíû ìûíà¹àí |
òå»: |
||||
DM = DQ |
× Dt , ì½íäà DQ1n– а¹ынны» сатылы ¼згерiсi. |
|
||||||||||
1П |
|
|
|
|
|
|
|
|
t |
|
|
|
t óàºûòûí Dt интервалымен n = |
|
á¼ëåìiç. ̽íäà Ì - m |
||||||||||
|
|
|
||||||||||
|
|
теңестіріледі, |
|
|
t × D |
DÌ |
||||||
шарыны» |
санымен |
áið |
|
шарды» алымûíà |
||||||||
¼ñiìøåñi, àë n - àëымыны» санына |
|
|
t |
|
|
шамасы с¸йкес келедi. |
||||||
|
|
|
|
|
|
|||||||
Dt
Осыны есепке ала отырып, мынаны аламыз:
Dt ® 0 æ¸íå DM
dM = Q áîë¹àíäûºòàí: dt
æ |
M |
ö |
t |
|
Dt |
; |
|||
р = ç |
|
÷ |
|
|
|
||||
è M + DM ø |
|
|||
® 0 шектеуде, - ln р = |
dM |
× |
t |
, àë |
|
|
|||
|
dt |
M |
||
|
Q |
×t немесе р = y = e- |
t |
||
- ln р = |
T |
; |
|||
M |
|||||
|
|
|
|
||
ì½íäàғы ó - араластыр¹ышта болу уаºыты t -дан асатын материал ¾лесi; ал t уаºытта араластыр¹ыш арºылы ¼тетiн
- |
t |
|
M |
|
|
|
|
||||
материалды» ¾лесi мына¹ан те»: 1 - e T . T = |
шамасы, |
||||
Q |
|||||
|
|
|
|
||
б¼лшектi» араластыр¹ышта болуыны» орташа уаºытына те». Осылайша, Q1P а¹ынны» сатылы ¼згеруi, бiрiншi ретi
дифференциалды те»деуге с¸йкес келетiн араластыр¹ышта¹ы б¼лiкшелер санын, экспоненциалды за» бойынша ¼згеруiн тудырады.
17

М.Д. Адамбаев, Т.С. Малдыбаева
Екi идеалды араластыр¹ыштан º½рал¹ан каскад те»деуiн º½райыº, егер кiрiс шамасы деп - каскадºа келтiрiлетiн а¹ында¹ы реагенттi» Ñ1 концентрациясын, ал шы¹ыс шамасы деп - каскадтан ¸кетiлетiн а¹ында¹ы Ñ3 концентрациясын алсаº, аралыº а¹ында¹ы концентрация –Ñ2.
Àëäûң¹ы мысалды» шешiмiне с¸йкес, бiрiншi араластыр¹ыш ¾шiн мына те»деудi жазу¹а болады:
|
|
|
|
|
T1 |
dС |
|
|
+ С2 |
= С1 ; |
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
dt |
|
|
|||||||||||||
екiншi араластыр¹ыш ¾шiн: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
T |
dC3 |
+ C |
|
= C |
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 dt |
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
||
|
|
Бiрiншi араластыр¹ышты» шы¹ыс шамасы екiшiсiне - кiрiс |
|||||||||||||||||||
øàìà áîëàтындықтан, |
dC2 |
|
|
|
|
d 2 C3 |
|
|
dC3 |
|
|
òå»äåóiíåí Ñ2 æ¸íå |
|||||||||
dt |
|
= T2 |
|
dt 2 + |
dt |
|
|
||||||||||||||
|
dС2 |
|
|
|
|
|
|
|
|||||||||||||
|
- ны алып тастап, мынаны аламыз: |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2C |
|
|
|
|
dC |
|
|
|
|
|
|||||||
|
|
T ×T |
|
|
3 |
+ (T + T ) |
|
|
3 |
|
+ C = C . |
(1.20) |
|||||||||
|
|
|
|
|
dt |
|
|||||||||||||||
1 2 |
dt 2 |
1 |
2 |
|
|
|
|
|
|
3 1 |
|
||||||||||
Араласуы жоº (ы¹ыстыру араластыр¹ышы) жинаºты» |
|||||||||||||||||||||
òå»äåóií º½рамыз. Сапалы материалды», мысалы |
кез келген |
||||||||||||||||||||
компоненттi» концентрациясы C1 (t ) òå» Q1 à¹ûíû, C2 (t ) сапасына ие жинаºта¹ы материал¹а тиiп, жинаº арºылы ¾стiнен астына ¼тедi. С2 (t ) сапасына ие Q2 = Q1 à¹ûí ¸êåòiëåäi. Кiрiс шамасы äåï - C1 (t ), шы¹ыс шамасы äåï - С2 (t)
алу керек. Жинаº Ì ºорымен сипатталады (1.6-сурет).
Б½л жа¹дайда С2 (t ) ¼çãåðiñi C1 (t) ¼çãåðiñiíå ºàðà¹àíäà
t = M уаºтына кешiгедi, сонда iзделiп отыр¹ан те»деу мына
Q
ò¾ðãå èå:
|
(t )= C |
(t -t ) = C |
æ |
M |
ö |
|
С |
çt - |
÷ . |
||||
|
||||||
2 |
1 |
1 |
ç |
Q |
÷ |
|
|
|
|
è |
ø |
18
