
adambaev_avtomatty
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Автоматты басқару теориясы |
|
|
|||
Бұл |
|
формулалар |
|
|
|
|
|
Фурье |
коэффициенттерін |
есептеген |
|||||||||
формулаларға ұқсас, |
бірақ бұл жерде sin пен cos функциялары l0 , |
|
|||||||||||||||||
l1 , … -мен ауыстырылған. Бұл дегеніміз – sin |
пен cos функциялары, |
|
|||||||||||||||||
ln - функциялары сияқты, толық ортогональді функциялар жүйесін |
|
||||||||||||||||||
құрайтындығына байланысты [12]. |
|
C |
|
|
|
|
|||||||||||||
2.10-кестеде бірінші алты C , |
C |
, C , …, |
коэффициенттерінің |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
5 |
|
|
|
|
жуық есептеулері келтірілген. Ол |
үшін 3,4,5,6 |
және 8 |
бағандарда, |
|
|||||||||||||||
сәйкес келетін Dti ; |
уақыт моменттері үшін, Лаггер функцияларының |
|
|||||||||||||||||
кестелік мәндері жазылған. Мысалы, l4 (7) = 0,392 -ге тең. Қалған алты |
|
||||||||||||||||||
бағанда x(t |
)×l |
(t ); |
x(t |
)×l |
|
(t ) және олардың қосындысы есептелген: |
|
||||||||||||
i |
0 |
i |
|
i |
1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
0 |
» |
24 |
x(t |
i |
)×l |
0 |
t( |
×)1 = 2,705; |
ü |
|
|
|
|
|||
|
|
|
|
å |
|
|
|
|
i |
|
|
ï |
|
|
|
|
|||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
24 |
|
|
|
)×l1 |
t(i |
×)1 =1,146; |
ï |
|
|
|
|
||||
|
|
» å x(t1 |
ï |
|
(2.102) |
|
|
||||||||||||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
» å24 |
x(ti |
)×l2 |
t(i |
×)1 =1,855; |
ï |
|
|
|
|
|||||||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
» å24 |
x(ti |
)×l3 |
t(i |
|
|
ý |
|
|
|
|
|||||
|
|
C3 |
×)1 = -7,513;ï |
|
|
|
|
||||||||||||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
C4 |
» |
24 |
|
( |
|
)× |
l4 |
( |
×) |
= - |
ï |
|
|
|
|
||
|
|
|
å x ti |
|
ti |
1 |
5,475;ï |
|
|
|
|
||||||||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
24 |
x(t |
|
)× l |
|
t( |
|
|
|
|
|
|
|||
|
|
C |
5 |
» |
i |
5 |
×)1 = -9,489.ï |
|
|
|
|
||||||||
|
|
|
|
å |
|
|
|
|
i |
|
|
þ |
|
|
|
|
|||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сонымен, талданып отырған сигналдың жуықтауы, Лаггердің |
|
||||||||||||||||||
еселі функцияларының қосындысы ретінде алынды: |
|
|
|
||||||||||||||||
|
x(t )» 2,705 ×l0 (t )+1,146 ×l1 (t )+1,855 ×l2 (t )- |
(2.103) |
|
|
|||||||||||||||
- 7,513 ×l3 (t )- 5,475 ×l4 (t )- 9,489 ×l5 (t )
x(t) сигналы мен оның спектральды тығыздығы арасындағы
байланыс бар екені белгілі [18, 414 бет]: |
|
|
|
|
|
|
|
||||||
S(w )= lim |
1 |
|
òT |
x(t )× e- jwt × dt |
|
2 |
» |
1 |
|
|
Tò x(t )×e- jwt × dt |
|
2 . (2.104) |
|
|
|
|
||||||||||
|
|
|
T |
||||||||||
T ®¥ T |
|
0 |
|
|
|
|
|
0 |
|
|
|||
Бұл байланыста бастапқы сигналдың Фурье түрлендіруі бар. Сонымен қатар, Лаггер функциясы үшін Фурье турлендіруі мына
түрге ие болатыны дәлелденген:
|
- w |
|
n |
|
|||
T |
(1 - jw) |
|
, (n = 0,1,2,3,4,5). (2.105) |
||||
Ln (jw )= òln |
(t )× e j t × dt = |
2 |
× |
|
|
|
|
(1 + |
n |
+1 |
|||||
0 |
|
|
|
jw) |
|
|
|
97
М.Д. Адамбаев, Т.С. Малдыбаева
Соңдықтан, X(t) сигналы Лаггердің еселі функцияларының қосындысы екенін ескеруге болады:
S (w )» 1 2,705 × L0 (jw )+1,146 × L1 ( jw )+1,855 × L2 (jw )-
T
-7,513× L3 ( jw)- 5,475 × L4 (jw)- 9,489 × L5 (jw)2 =
=1 × 2,705 × 
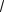 2 ×(1 - jw )0 + 1,146 ×
2 ×(1 - jw )0 + 1,146 × 
 2 ×(1 - jw) + 1,855 ×
2 ×(1 - jw) + 1,855 × 
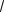 2 × (1 - jw)2 -
2 × (1 - jw)2 -
25 (1 + jw ) (1 + jw)2 (1 + jw)3
- |
7,513 × |
|
|
×(1 - jw)3 |
- |
|
5,475 × |
|
|
|
× (1 - jw )4 |
|
|
9,489 × |
|
|
|
× (1 - jw )5 |
|
2 |
|
|
|
(2.106) |
||||||||||||||||||||||||||||||||
|
2 |
|
|
2 |
- |
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(1 + jw )4 |
|
|
|
|
(1 + jw)5 |
|
|
|
|
|
(1 + jw)6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
мұнда Т= 25 мин ( 2.10-кестеден). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Егер (2.103) қатардың алты емес, |
|
|
екі мүшесін ғана алсақ, |
|
онда |
|||||||||||||||||||||||||||||||||||||||||||||||||
ізделген спектральдық тығыздық, өрескел болса да, келесі өрнекпен |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
бағаналады: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,62 × (1 - jw ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S (w )» |
1 |
|
3,82 |
+ |
|
2 . |
|
|
|
|
|
|
|
|
|
|
(2.107) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
1 + jw |
|
|
(1 + jw)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Бұл өрнекті, көрнекілік үшін төменде қолданамыз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
(2.107) түрлендіру өте қарапайым және күрделі(2.106) өрнегін |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
түрлендіруді түсінуге мүмкіндік береді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Одан арғы есептеулер, S(ω)-ны ыңғайлы түрде жазу үшін қажетті |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
тепе-теңдік түрлендірулерді жүргізуге негізделген. Бұл |
|
кезде біз |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
жорамал сандардан толық босатыламыз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
(2.107) |
|
|
өрнектегі w |
|
бойынша |
|
|
комплексті |
|
|
функция |
модулінің |
||||||||||||||||||||||||||||||||||||||||||
квадратын табу қажет. Бөлшектің |
|
|
|
бөліміндегі |
жорамал |
|
саннан |
|||||||||||||||||||||||||||||||||||||||||||||||||
босатылып, нақты және жорамал бөліктерге бөліп, модульді анықтап, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
оны квадрат дәрежеге шығарамыз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(w )» |
1 |
|
|
3,82 ×(1 - jw) |
+ |
1,62 ×(1 - jw) |
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + w2 |
|
|
|
(1 + w2 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
0,04 |
|
|
|
|
|
|
- jw)×(1 + w |
2 |
)+1,62 ×(1 |
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
× |
3,82 ×(1 |
|
- jw) |
|
|
= |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
(1 +w 2 )4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
0,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
|
× |
|
3,82 × (1 + w2 )- 3,82 × jw × (1 + w2 )+1,62 × |
|
1 - 3 jw - 3w2 - jw3 |
|
2 |
= |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
(1 + w2 )4 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
|
|
0,04 |
|
× |
|
(5,44 -1,04 ×w2 )- j 8(,68 ×w + 5,44 ×w3 ) |
|
2 |
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
(1 + w2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
0,04 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
= |
|
×[(5,44 -1,04 ×w 2 ) + 8(,68 ×w + 5,44w3 ) ]. |
|
|
|
(2.108) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
(1 +w 2 )4 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
98

Автоматты басқару теориясы
2.10-кесте
ti, мин |
x(ti), åä |
l0(ti) |
l1(ti) |
l2 (ti) |
l3(ti) |
l4(ti) |
l5(ti) |
x(ti) |
x(ti) l1(ti) |
x(ti) l2 (ti) |
x(ti) l3(ti) |
x(ti) |
x(ti) l5(ti) |
|
|
|
|
|
|
|
l0(ti) |
|
|
|
l4(ti) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
1,20 |
1,414 |
-1,414 |
1,414 |
-1,414 |
1,414 |
-1,414 |
1,700 |
-1,700 |
1,700 |
-1,700 |
1,700 |
-1,700 |
1 |
0,20 |
0,520 |
-0,520 |
0,520 |
-0,173 |
0,173 |
-0,381 |
0,104 |
-0,104 |
-0,104 |
0,035 |
0,035 |
0,076 |
2 |
4,00 |
0,191 |
0,574 |
0,191 |
-0,447 |
0,191 |
0,166 |
0,764 |
2,296 |
0,764 |
-1,788 |
0,764 |
0,664 |
3 |
2,80 |
0,070 |
0,352 |
0,493 |
-0,070 |
-0,352 |
0,267 |
0,196 |
0,982 |
1,380 |
-0,070 |
-0,920 |
0,748 |
4 |
-1,80 |
0,026 |
0,181 |
0,443 |
0,319 |
-0,250 |
-0,205 |
-0,047 |
-0,326 |
-0,796 |
-0,575 |
0,450 |
0,370 |
5 |
-1,60 |
0,009 |
0,086 |
0,295 |
0,435 |
0,105 |
-0,327 |
-0,014 |
-0,138 |
-0,472 |
-0,696 |
-0,168 |
0,524 |
6 |
1,50 |
0,003 |
0,039 |
0,172 |
0,375 |
0,340 |
-0,086 |
0,005 |
0,059 |
0,258 |
0,563 |
0,510 |
-0,129 |
7 |
-3,20 |
0,001 |
0,017 |
0,092 |
0,263 |
0,392 |
0,182 |
-0,003 |
-0,055 |
-0,294 |
-0,843 |
-1,250 |
-0,583 |
8 |
-5,70 |
0,000 |
0,007 |
0,046 |
0,168 |
0,334 |
0,347 |
0,000 |
-0,040 |
-0,262 |
-0,600 |
-1,900 |
-1,973 |
9 |
-7,90 |
|
0,003 |
0,022 |
0,094 |
0,242 |
0,360 |
|
-0,024 |
-0,174 |
-0,743 |
-1,910 |
-2,840 |
10 |
-12,00 |
|
0,001 |
0,010 |
0,051 |
0,158 |
0,310 |
|
-0,012 |
-0,120 |
-0,612 |
-1,894 |
-3,722 |
11 |
-4,002 |
|
0,000 |
0,010 |
0,026 |
0,095 |
0,226 |
|
0,000 |
-0,020 |
-0,104 |
-0,380 |
-0,904 |
12 |
-2,50 |
|
|
0,005 |
0,013 |
0,054 |
0,152 |
x(ti )× |
|
-0,005 |
-0,032 |
-0,135 |
-0,380 |
13 |
0,40 |
|
|
0,002 |
0,006 |
0,030 |
0,095 |
|
0,000 |
0,002 |
0,012 |
0,038 |
|
14 |
-0,50 |
|
|
0,001 |
0,003 |
0,016 |
0,057 |
l0 (ti )= 0 |
x(ti )× l1 (t1 )= |
|
-0,002 |
-0,008 |
-0,029 |
15 |
3,60 |
|
|
0,000 |
0,001 |
0,008 |
0,032 |
|
0,004 |
0,029 |
0,115 |
||
|
|
|
|
||||||||||
16 |
8,20 |
|
|
|
0,001 |
0,004 |
0,018 |
|
= 0 |
|
0,008 |
0,033 |
0,147 |
17 |
6,50 |
l0(ti)=0 |
|
|
0,000 |
0,002 |
0,009 |
|
|
x(ti )×l2 (t2 )= |
0,000 |
0,013 |
0,059 |
18 |
5,60 |
|
l1(ti) =0 |
|
|
0,001 |
0,005 |
|
|
|
0,006 |
0,028 |
|
19 |
2,90 |
|
|
|
0,000 |
0,002 |
|
|
= 0 |
|
0,000 |
0,006 |
|
20 |
-2,90 |
|
|
|
|
|
0,001 |
|
|
|
|
-0,003 |
|
|
|
|
|
|
|
|
|
x(ti )×l3 (t3 )= |
|
||||
21 |
-0,50 |
|
|
l2 (ti)=0 |
|
|
0,001 |
|
|
|
|
-0,001 |
|
22 |
3,50 |
|
|
|
l2 (ti)=0 |
|
0,000 |
|
|
|
= 0 |
|
0,000 |
23 |
7,00 |
|
|
|
|
|
0,000 |
|
|
|
|
|
|
24 |
11,00 |
|
|
|
|
l4 (ti)=0 |
0,000 |
|
|
|
|
|
|
|
|
|
|
|
|
å |
|
2,705 |
1,146 |
1,855 |
-7,513 |
-5,475 |
-9,489 |
99

М.Д. Адамбаев, Т.С. Малдыбаева
Мұнда белгілі қатынас қолданылған:
A(w)+ jB(w )2 = [
 A2 (w)+ B2 (w)]2 = A2 (w )+ B 2 (w).
A2 (w)+ B2 (w)]2 = A2 (w )+ B 2 (w).
Табылған спектрлік тығыздық w бойынша жұп функция, оның графигі - ординат осі бойынша симметриялы. Кездейсоқ сигналдардың спектрлік тығыздықтары, корреляциялық функциялар сияқты информация беріп, объектінің динамикалық қасиеттерін бағалау үшін қолдануы мүмкін. Мысалы:
|
W ( jw |
|
)= |
S2 |
(w) |
. |
(2.109) |
|
|
||||||
|
|
|
|
S1 |
(w ) |
|
|
|
|
|
|||||
Бұл формула объектінің комплексті беріліс коэффициентінің модулін, шығыс S2(ω) мен кіріс S1(ω) спектрлік тығыздықтар арқылы бағалайды.
Біз қарастырып отырған статистикалық динамика әдістерінде есептеу процедуралары күрделі, өйткені Винер-Хопфтың интегралды теңдеулерін есептеу керек. Ал бұл өз кезегінде импульсті өтпелі
функцияны h(t) береді. Содан соң, h(t)-дан объектінің беріліс функциясын анықтайды. Осы процедураларды, h(t)-ны есептемей, қарапайым етуге бола ма? деген сұрақ туады.
Теңдеуі мына түрдегі объект үшін:
a0 x2(n ) + a1 x2(n-1) + ... + an-1 x2(1) + x2 = в0 х1 +в1 х1(1) + ... + вm x1(m )
келесі теңдік дұрыс:
a0 × R21(n)(t i |
)+ a1 × R21(n-1)(ti )+ ... + an × R21(t i )= |
|||||||||
= â |
× R |
(t |
i |
)+ â |
× R (1 )(t |
i |
)+ ... + â |
× R(m )(t |
i |
) |
0 |
1 |
|
1 |
1 |
m |
1 |
|
|||
немесе:
a0 × R2(n)(ti )+ a1 × R2(n-1)(ti )+ ... + an × R2 (ti )= = â0 × R12 (ti )+ â1 × R12(1 )(ti )+ ...+ âm × R12(m )(ti )
(соңғы жолда сигнал кері бағытта жүреді).
100
|
|
|
|
|
|
Автоматты басқару теориясы |
|
||||
Бұл |
теңдіктер |
мынадай |
ереже бер: едігер корреляциялық |
||||||||
функция оның кірісі болса, |
өзара корреляциялық функция – сызықты |
||||||||||
теңдеудің шығысы болады. Оларды, объект теңдеуінің ізделетін |
|||||||||||
коэффициенттерін |
|
анықтау |
үшін |
қолдануға |
болады. Ол |
үшін |
|||||
эксперимент арқылы R2(τ) мен R12(τ)-ды (немесе R1 мен R21-ні) табады, |
|||||||||||
содан соң R1 мен R12 мәндерін түрлі ti |
кезінде, теңдіктердің біреуіне |
||||||||||
қояды. Осы операцияны белгісіз коэффициенттер неше болса, сонша |
|||||||||||
рет қайталайды. Бұл ai , вi |
коэффициенттерін анықтайтын, |
сызықты |
|||||||||
алгебралық теңдеулер жүйесін береді. |
|
|
|
|
теңt |
||||||
Теңдіктерде, |
белгісіз |
коэффициенттердің |
санына , |
||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
нүктелерін алу керек. Дәлдікті жоғарылату үшін, ең кіші квадраттар |
|||||||||||
әдісін қолданып, |
ti |
санын көбірек |
алуға |
болады. Әрі |
дискретті |
||||||
нүктелерді |
емес, |
τmin<τ<τmax |
|
интервалында |
|
корреляциялық |
|||||
функциялардың үздіксіз кесінділерін қолдануға болады. Бұл кезде ең |
|||||||||||
кіші квадраттар әдісіндегі қосындылау операциясын– интегралдау |
|||||||||||
операциясымен ауыстырады. |
|
|
|
|
|
|
|
||||
2.4.5 Спектральдық тығыздықтарды қолданып, объектінің |
|||||||||||
|
комплексті (беріліс) функциясын есептеу |
|
|
|
|||||||
Объектінің стационарлы жұмыс режимінде біршама уақыт |
|||||||||||
аралығында, кіріс x1(t ) |
және |
шығысx2 (t ) сигналдарының орта |
|||||||||
мәннен ауытқулары тіркелген. Ал кіріс сигналының спектральдық |
|||||||||||
тығыздығы S1(ω) (ω бойынша жұп нақты функция) мен кіріс пен |
|||||||||||
шығыс |
сигналдарының |
арасындағы |
|
өзара |
|
спектральд |
|||||
тығыздық |
S21(jω) |
(ω |
бойынша |
комплексті |
функция) есептелген: |
||||||
S21(jw ) = K (w )+ jM (w ).
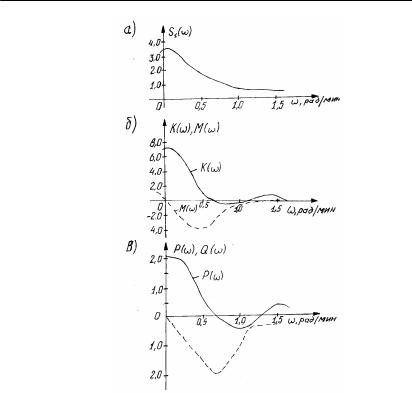
S1(ω), K(ω), M(ω) графиктері 2.9а,ә -суреттерінде көрсетілген. Берілген графиктер бойынша объектінің комплексті күшейту
коэффициентін W(jω) (беріліс функциясын) есептеу қажет. S1(ω)-ны есептеуді 2.4.2-ден қара.
Комплексті күшейту коэффициентін нақты және жорамал жиіліктік сипаттамалар арқылы көрсетеміз [13]:
W(jω) =P(ω)+jQ(ω).
101
Адамбаев, Т.С. Малдыбаева
2.9-сурет. Статистикалық әдістер бойынша жиіліктік сипаттамаларды есептеу үшін
Есептеулерді төмендегі формулалар бойынша жүргізуге болады:
P(w )= |
K (w) |
; |
Q(w )= |
M (w) |
. |
(2.110) |
|
|
S (w ) |
|
S |
(w ) |
|
||
1 |
|
1 |
|
|
|
||

Автоматты басқару теориясы
3

Автоматты басқару теориясы
2.11-кесте
wi , рад/мин |
0,00 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
K(ωi) |
7,3 |
7,1 |
6,2 |
4,3 |
2,5 |
1,0 |
0,2 |
-0,1 |
-0,2 |
-0,25 |
-0,3 |
-0,2 |
-0,0 |
0,1 |
0,2 |
|||
M(ωi) |
0,0 |
- |
- |
-3,3 |
-3,8 |
-3,8 |
-3,3 |
-2,3 |
-1,4 |
-0,8 |
-0,3 |
-0,26 |
-0,24 |
-0,22 |
-0,2 |
|||
|
|
|
|
|
1,1 |
2,3 |
|
|
|
|
|
|
|
|
|
|
|
|
S1(ωi) |
3,5 |
3,7 |
3,0 |
2,6 |
2,2 |
1,8 |
1,5 |
1,25 |
1,0 |
0,8 |
0,65 |
0,6 |
0,56 |
0,53 |
0,5 |
|||
P(w )= K (w) |
2,08 |
2,07 |
2,06 |
1,65 |
1,14 |
0,556 |
0,13 |
-0,08 |
-0,20 |
-0,34 |
-0,46 |
-0,33 |
0,0 |
0,05 |
0,4 |
|||
|
S1 (w |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(w )= |
M (w ) |
|
0,0 |
-0,298 |
-0,77 |
-1,27 |
-1,73 |
-2,11 |
-2,2 |
-1,84 |
-1,4 |
-1,0 |
-0,46 |
-0,44 |
-0,42 |
-0,41 |
-0,4 |
|
|
S (w ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
