разложение определителя по элементам некоторого ряда. При решении задач АЗ-1.2 и АЗ-1.3 рекомендуется воспользоваться правилами проведения операции над матрицами и формулой вычисления обратной матрицы к заданной.

Пример1. Вычислить определители: а)

(м-д Саррюса)

Пример 2. Вычислить определитель методом разложения .

Решение.Разложим этот определитель по элементам первой строки:

Пример 3.Найти произведение матриц А и В: С=АВ, где,.

Матрица А имеет 3 столбца, а матрица В - 3 строки, значит произведение АВ существует. Из вышеизложенного ясно, что матрица С будет содержать две строки и четыре столбца. Вычислим все ее элементы: с₁₁=2·3 + 1·5 + 3·(-1)=8; с₁₂=2·2 + 1·0 + 3·2=10;с₁₃=2·4 + 1·2 + 3·5=25; с₁₄=2·1 + 1·3 + 3·4=17; с₂₁=4·3 + (-2)·5 + 5(-1)=-3; с₂₂=4·2 + (-2)·0 + 5·2=18; с₂₃=4·4+(-2)·2+5·5=37; с₂₄=4·1+(-2)·3+5·4=18. Следовательно,

Пример 4. Дана матрица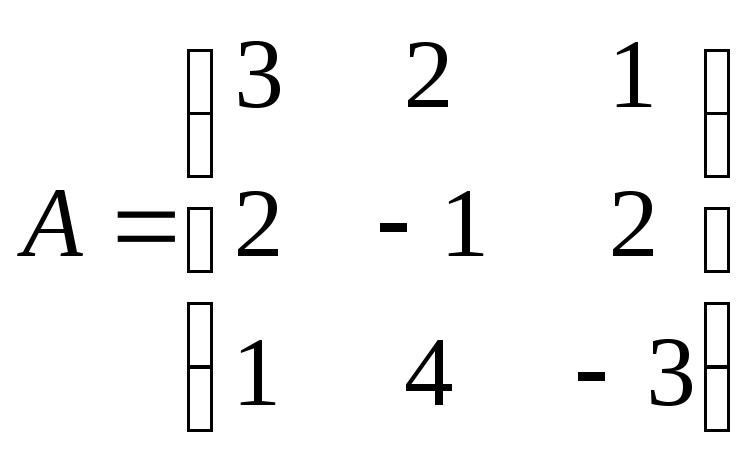. Вычислить обратную матрицу А^-1.

Решение.1). Вычислим

Матрица А невырожденная, значит обратная матрица существует.

2). Вычислим алгебраические дополнения всех элементов матрицы А: А_ij=(-1)^i+j M_ij

=-5 , ,,

, ,,

, ,

3). Запишем А^-1:

4). Проверка правильности вычисления.

Пример 6.Вычислить ранг матрицы.

Вычислим все миноры 3-го порядка. Их всего четыре.

;

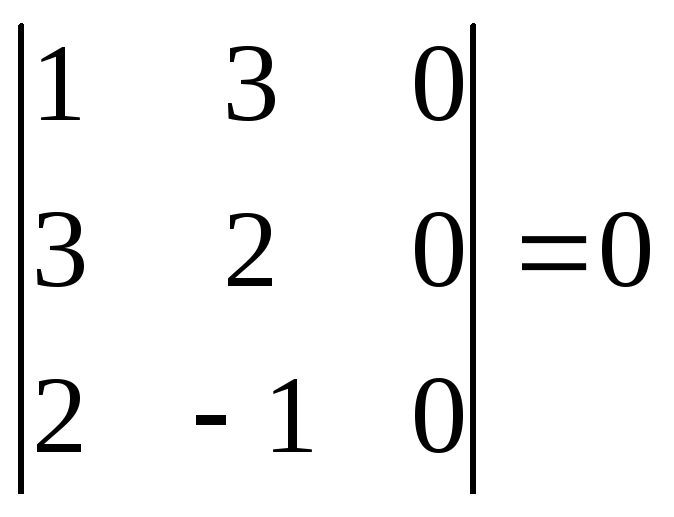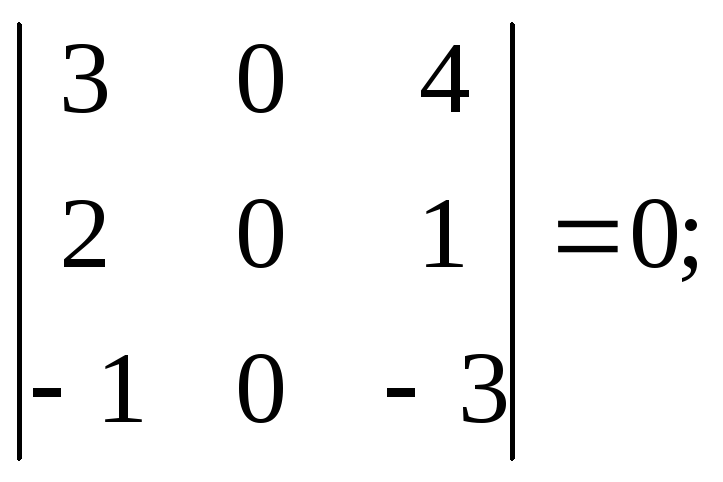
Теперь вычислим минор 2-го порядка Так как существует ненулевой минор второго порядка, то r (A) = 2.

Системы линейных алгебраических уравнений.

Задания. АЗ-1.4: [14] , часть1, №№1-3, 5.

Методические рекомендации. Прежде чем решать систему линейных алгебраических уравнений (СЛАУ) нужно исследовать ее на совместность. Если для системы ито можно использовать формулы Крамера или матричный метод. Если жеито целесообразно пользоваться алгоритмом метода Гаусса.

Пример 3: Исследовать и решить систему уравнений методом Гаусса.

Решение: Преобразуем расширенную матрицу

~

rangA=rangB=2, следовательно, система совместна(теорема Кронекера-Капелли).

r=2; n=4; r<n, значит система имеет бесконечное множество решений.

На самом деле, последняя матрица соответствует системе

Определитель из коэффициентов при переменных х₁ и х₂не равен нулю, след-но, эти переменные можно взять в качестве базисных. Переменные х₃и х₄ являются свободными. Из последнего уравнения находим: х₂=2-0,4х₃+х₄, подставив его в первое уравнение имеем х₁=9+0,2х₃-х₄.

Итак, решение системы: х₁=9+0,2х₃-х_4, х₂=2-0,4х₃+х₄.

Придавая х₃и х₄различные значения, получим бесконечное множество решений.

Замечание: в качестве базисных можно выбрать и другие пары переменных, например, х₁ и х_3.

Осн. лит. 12,[9-59],14, [27-33]

Доп.лит. 29, [189-192].

Контрольные вопросы:

1. Какие свойства определителей используются при их вычислении? Укажите основные правила вычисления определителей.

2. Приведите основные операции над матрицами. Как умножить матрицу на число? Как перемножаются матрицы?

3. Какими методами вычисляется ранг матрицы? Какой цели служит ранг матрицы?

4. В каких случаях для решения системы линейных уравнений можно применить метод Крамера и матричный?

Практическое занятие №2.

Векторная алгебра. Скалярное, векторное и смешанное произведение векторов. Плоскость. Уравнения прямой на плоскости. Прямая в пространстве. Угол между прямыми. Прямая и плоскость.

Задания. АЗ-2.1: [14], часть 1, №№1-8, АЗ-2.2 [14] ,часть 1, №№1-7, АЗ-2.3 [14], №№1-7.

Методические рекомендации. При решении задач рекомендуется использовать правила вычисления координат векторов их длин, а также линейные операции над векторами. Для вычисления скалярного произведения использовать его определение или формулу вычисления через координаты перемножаемых векторов. При нахождении векторного произведения необходимо учитывать условия, которым должны удовлетворять данные вектор и формулу вычисления векторного произведения через их координаты. При вычислении смешанного произведения трех векторов необходимо использовать правила вычисление определителя третьего порядка.

Пример 1. Вычислить скалярное произведение векторов, если.

Решение. По определению скалярного произведения получим .

Пример 2. Пусть найти.

Решение.

Пример 3. Даны точкиинайти смешанное произведение векторови.

Решение. и,.

Плоскость и прямая в пространстве.

Задания. АЗ-3.1: [14] , часть 1, №№. 1-4, АЗ-3.2: [14], №№. 1-3.

Методические рекомендации. Уравнение плоскости в пространстве составляется в зависимости от способа ее задания. При составлении уравнения прямой в пространстве учитываются координаты направляющего вектора. Взаимное расположение прямых и плоскостей в пространстве определяется расположением их направляющих и нормальных векторов. А углы между прямыми и плоскостями определяются через углы между этими векторами.

АЗ: [11], №2.141,2.143,2.145,2.147,2.153,.2.180,2.198.

Пример.Дана плоскость. Привести следующие уравнения плоскости: а) уравнения в отрезок на осях; б) нормальное уравнение плоскости; в) уравнение плоскости с угловыми коэффициентами; г) параметрические уравнения плоскости; д) векторное уравнение плоскости.

Решение:

а) разделим общее уравнение плоскости на свободный член: ,получаемуравнение в отрезках на осях.б) вычислим длину нормального вектораплоскости;длина ===

Разделим общее уравнение плоскости на :

;

получаем - нормальное уравнение плоскости

в) выразим черези: ; ; .

получаем: уравнение с угловым коэффициентом.

г) Запишем следующие уравненияполучаем параметрыи

тогда перепишем уравнение

получаем: , где,- действительные параметры

параметрические уравнения плоскости.

д) запишем параметрические уравнения в векторном виде.

получаем: векторное уравнение плоскости.

ДЗ: [11] №2.142, 2.144, 2.146, 2.148, 2.154, 2.156, 2.199, 2.181.

Осн. лит. 14 , часть 1, [59-69].

Контрольные вопросы:

1. Привести формулу вычисления угла между двумя векторами через скалярное произведение этих векторов.

2. Какие свойства скалярного и векторного произведения используются при их вычислении?

3. Как вычисляются направляющие косинусы заданного вектора?

4. Какие условия должны выполняться для коллинеарности векторов?

5. Какой вид уравнения прямой определяет отрезки отсекаемые на осях координат?

6. Как определить угол между двумя плоскостями?

7. Привести условие параллельности и условие перпендикулярности плоскостей.

8. Как определить угол между прямой и плоскостью?

Практическое занятие №3.

Введение в анализ. Функция. Вычисление пределов. Непрерывность.

Задания. АЗ – 5.1: [14], часть1, №№ 1-3., АЗ 5.2: [14], часть 1, №№ 1-5, АЗ 5.3: [14], часть 1, №№ 1-4, АЗ 5.4: [14] , часть 1, №№ 5-7.

Методические рекомендации. При решении практических задач данной темы знать основные понятия функции – область определения, множество значений, четность и нечетность, периодичность и т.д. При нахождении предела функции используются методы непосредственного вычисления и устранения неопределенностей путем преобразования данного выражения, предельных переходов, использования замечательных пределов и их следствий. Непрерывность функции в точке устанавливается согласно определению. Для анализа возможных точек разрыва вычисляются односторонние пределы. При нахождении производной функции необходимо применять правила дифференцирования и таблицу производных. Производнаяn-го порядка определяется дифференцированием производнойn-1 го порядка. Согласно определению дифференциала можно найти дифференциала любого порядка.

Пример.Сравнить бесконечно малые:с бесконечно малой.

Решение. . Следовательно, иодного порядка.

Пример. Найти следующий предел: .

Решение.Числители и знаменатели дробей будем заменять эквивалентными бесконечно малыми.

~,~тогда.

Производная и дифференциал

Задания АЗ 6.1: [14], часть 1, №№ 1,2, АЗ 6.2: [14], часть 1, №№ 1-3, АЗ 6.3: [14], часть 1, №№ 1-3 АЗ 6.4: [14] ,часть 1, №№ 1-3.

Пример. Найтиесли

Решение. Вычислим:

Тогда

Пример. Найтиесли

Решение. НаходимТогда

Пример. Найти .

Решение.

2.2 Найти если

Решение.

Осн.лит.: 14, часть 1, [156-165].

Контрольные вопросы:

1. Как найти производную функции заданной параметрически?

2. В чем заключается геометрический и механический смысл производной первого порядка?

3. Сформулируйте алгоритм метода логарифмического дифференцирования.

Практическое занятие № 4. Неопределенный интеграл. Определенный интеграл.

А3 – 8.1 [14], часть 1, № 1-8, А3 – 8.2 [14], часть 1, № 1-8, А3 – 8.4 [14], часть 1, № 1-4. А3 – 8.5 [14], часть 1, № 1-3. Задания: А3 – 8.6 [14], часть2, № 1-5, А3 – 8.7 [14], часть2, № 1-4, А3 – 8.8 [14], часть2, № 1-5.

Методические рекомендации. При нахождении неопределенных интегралов используются их свойства и таблица интегралов. Для приведения заданного интеграла к табличному применяется методы подведения под знак дифференциала и метод подстановки. При использовании метода интегрирования по частям нужно правильно представить подынтегральное выражение в виде произведения двух сомножителейи.

Пример.1Найти

Пример2: Найти. Здесь выгодно продифференцироватьlnx, т.к. тогда получится степенная функция, которая проще логарифмической, а второй множительx²dxинтегрируем.,, , , +С, для удобства С=0, т.к. нас устроит любая первообразная.

При интегрировании дробно-рациональную функцию можно представить в виде суммы многочлена и простейших дробей. При разложении дроби на простейшие дроби удобно использовать метод неопределенных коэффициентов. Для избавления от иррациональностей нужно выбрать правильную подстановку, которая позволит привести заданный интеграл к табличному.

Пример3:

=

=

Если знаменатель не имеет действительных корней, то в нем выделяют полный квадрат и производят замену переменной.

Пример 4:

При интегрировании неправильной рациональной дроби необходимо выделить целую часть и только потом интегрировать многочлен и правильную дробь.

Рассмотрим интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.В частных случаях один из показателей (mилиn) может равняться нулю. Пустьmиn– целые неотрицательные числа. Рассмотрим случай, когда хотя бы один из показателейmиnесть числонечетное. В этом случае интеграл вычисляетсяметодом замены переменной: отделяем от нечетной степени один множитель и полагаем кофункцию этого множителя равной новой переменнойt.

Пример5:

В случае, когда оба показателя mиn– числачетные, используютсяформулы понижения степени:

Пример6:

Определенный интеграл.

Задания: А3 – 9.1 [14], часть 2, № 1-8, А3 – 9.2 [14], часть 2, № 6-10, А3 – 9.3 [14], часть 2, № 1-4, А3 – 9.4 [14], часть 2, № 4-6.

Методические рекомендации. При вычислении определенного интеграла с известной первообразной нужно использовать формулу Ньютона-Лейбница.

Пример. Найти интеграл отв пределах от 1 до 3.

Решение.

Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к прежней переменной.

Осн. лит.:14 , часть 2, [15-34]; часть 2б [137-205]; 14, часть 2, [35-48].

Доп. лит.:26, [148-164].

Контрольные вопросы:

1. Как внести множитель под знак дифференциала?

2. Как выделить целую часть у неправильной дроби подынтегральной функции?

3. Какая подстановка является универсальной для интегрирования тригонометрических функции?

4. Приведите формулу Ньютона – Лейбница.

Практическое занятие №5. Функция нескольких переменных.

АЗ: 26, [1850,1858,1899,1907,1926,2017,2030].

Пример .Дана функция f( x,y ) = x² - 2x + 3y² и точка М₀ ( 3,1 ). Требуется: а) найти линию уровня функции z = f( x, y ), проходящую через точку М₀ ; б) найти grad z( M₀ ) и построить его; в) вычислить в точке М₀ производную функции z = f( x,y ) по направлению grad z( M₀ ); г) вычислить в точке М₀ производную функции z = f( x,y ) по направлению вектора M₀ N, где N( 2,2 ); д) найти и построить линию уровня функции z = f( x,y ), проходящую через точку М₁, где = grad z( M₀ ); указать какое свойство градиента здесь иллюстрируется.

Решение:а) Линия уровня данной функции, проходящая через точку М₀ ( 3,1 ), имеет уравнение f( x,y ) = f( 3,1 ). Отсюда, x² - 2x +3y² = 6 - уравнение искомой линии уровня. Выделив полный квадрат, приведем уравнение к виду ( x-1)² + 3y² = 7 или ( x-1)² /7 + y² /( 7/3 ) = 1 Это каноническое уравнение эллипса с центром в точке ( 1,0 ) и полуосями a = . График изображен на рисунке 1

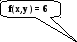У M₁

N(2,2)

M₀(3,1)

0 X

Рис.1

б) grad z( M₀ ) = ( ) , grad z( M₀ ) = = ( 4,6 ); в) Обозначив =. По свойствам градиента; ; г) Обозначимпо условию N( 2,2 ), поэтому.Итак,= ( -1,1 ); тогда орт этого вектораПо свойствам градиента Тогда, . Причем,.Это естественно, так как в точке М₀ производная по направлению градиента имеет наибольшее значение, равное grad z( M₀ ). д) Найдем сначала координаты точки М₁. Так как вектор = (4,6) и М₀ ( 3,1 ), то точка М₁ (7;7). Линия уровня, проходящая через точку М₁( 7,7 ) имеет уравнение f( x,y ) = f( 7,7 ) =182. Отсюда, x² - 2x +3y² = 182 или ( x-1)² +3y² = 183 или . Это эллипс с центром в точке О( 1,0 ) и полуосями а =183 13.53, b= 61 7.81. Дуга этого эллипса, лежащая в первой четверти изображена на рис.1. Итак, при переходе от точки М₀ ( 3,1) к точке М₁( 7,7) по направлению градиента функции z = f( x,y ) значение этой функции возрастает от 6 до 182. Это иллюстрирует свойство градиента, состоящее в том, что направление градиента является направлением наискорейшего возрастания функции.

Осн.лит. 14, часть 2, [208-222]; Доп.лит. 26, [191-210].

Контрольные вопросы:

1. Дайте определение линии и поверхности уровня функции нескольких переменных.

2. Приведите формулу производной функции нескольких переменных по направлению.

3. Перечислите свойства градиента функции нескольких переменных.

Практическое занятие № 6. Дифференциальные уравнения первого порядка

Задания. АЗ-11.1 [14] часть 2, №№1-7, АЗ-11.2 [14], №№1-7.

Методические рекомендации. При нахождении решения линейного уравнения, можно пользоваться формулой.

Пример 1. Решить уравнения с разделяющимися переменными 1). Разделяем переменные;;;;

2) ;;;;;;.

Пример 2 . . Справа стоит однородная функция нулевого измерения, следовательно, это однородное уравнение. Делаем замену. Тогда;;;;.

Разделяя переменные, получим ;.

Отсюда, интегрируя находим

;;.

Подставляя , получим общий интеграл исходного уравнения.

Пример 3. .

Переходить к виду, разрешенному относительно производной, не обязательно. ,,. Подставляем эти значения в уравнение.,. Разделяя переменные, получим

,,,. Подставляя вместо, получим,,- общее решение.

Пример 4.Решить уравнение

;;;;;

;;;;;;;

;;.

Осн. лит. 14, часть 2, [243-259]. Доп. лит. 29, [315-320], [321-330].

Контрольные вопросы:

1. Общее решение дифференциального уравнения

2. Дифференциальные уравнения с разделяющимися переменными

3. Линейные дифференциальные уравнения первого порядка