10546

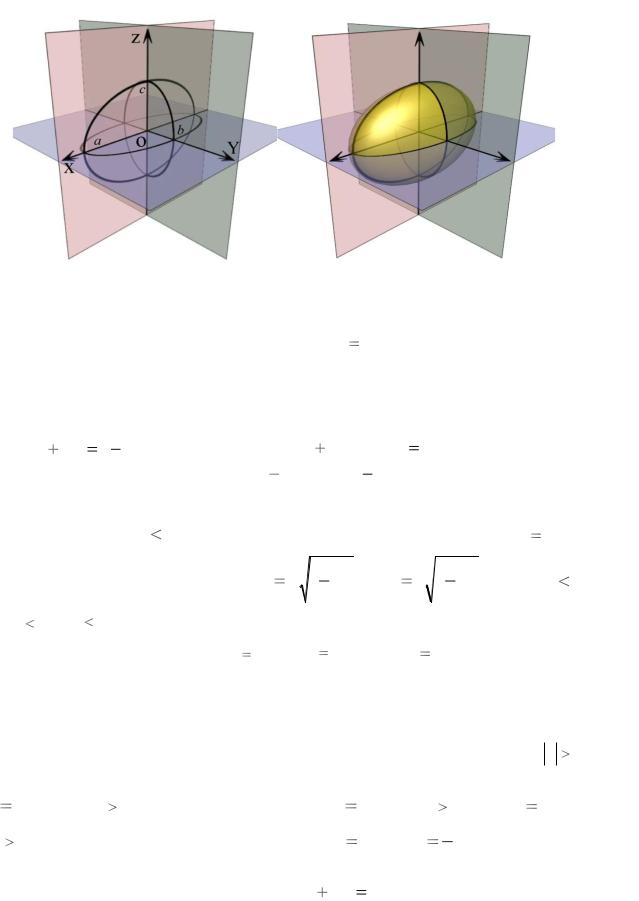
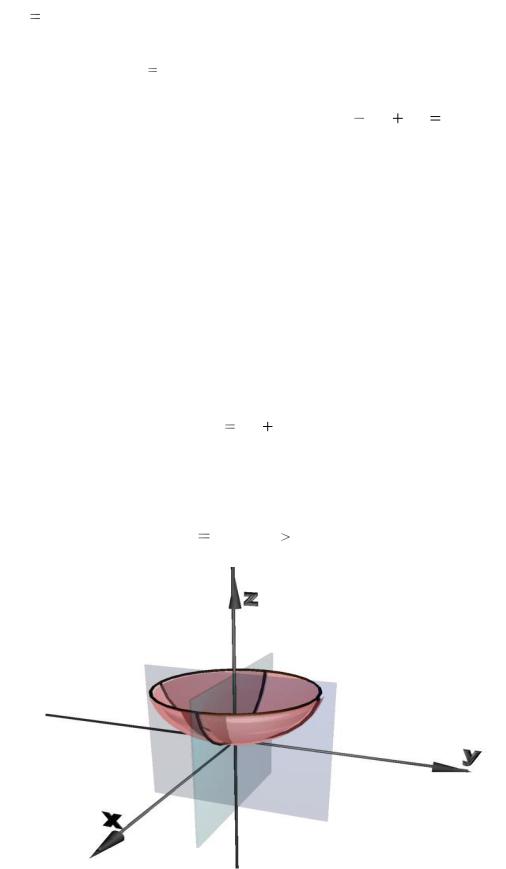
Рис. 28.2

Рассмотрим произвольную плоскость z h (где h – любое число), параллельную xOy . Сечение исходной поверхности (28.1) этой плоскостью

задаѐтся уравнением

«самый крупный» эллипс образуется в сечении координатной плоскостью xOy . Аналогичная картина получается в сечениях поверхности (28.1)

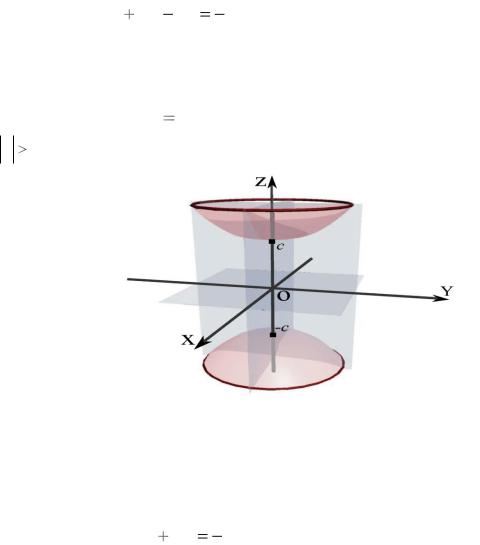
плоскостями, параллельными координатным плоскостям xOz и yOz . Отметим, что на плоскости нет точек, отвечающих условию z c .

Т.е. у поверхности, которую мы строим, нет пересечения с плоскостями

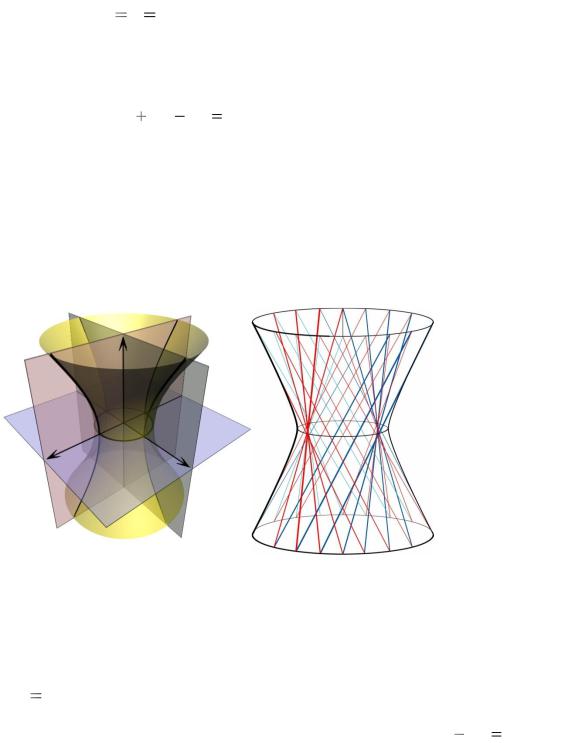
Если a b , то конус становится поверхностью вращения (в этом случае он называется круговым конусом) и может быть получен вращением

Особенностью конуса является то, что любое его сечение плоскостью, не проходящей через вершину, есть эллипс, гипербола или парабола (в зависимости от наклона секущей плоскости). Поэтому эти классические линии со времѐн Древней Греции называют коническими сечениями. Часто встречаясь в явлениях природы и деятельности человека, эти линии приобрели особое значение после открытия, сделанного из наблюдений И.Кеплером в 1609 году и теоретически обоснованного И.Ньютоном в 1687 году: планеты и кометы Солнечной системы движутся по коническим сечениям, в одном из фокусов которого находится Солнце.

28.4. Параболоиды. Рассмотрим уравнение эллиптического пара-

болоида

где параметры p и q положительны. В сечениях координатными плоскостями xOz и yOz поверхности, определяемой этим уравнением, получаются параболы, а в сечениях z h при h 0 –эллипсы (рис. 28.6).

Рис. 28.6

206

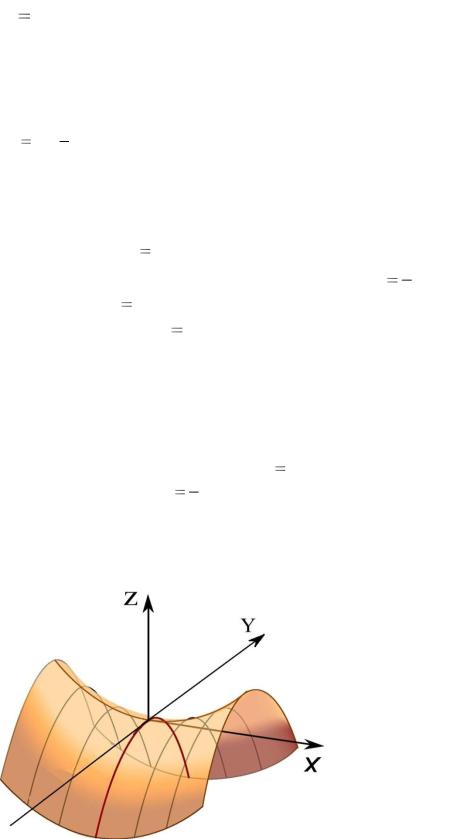
Эллиптический параболоид обладает двумя плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями xOz и yOz ). При p q параболоид становится поверхностью вращения

(в этом случае он называется параболоидом вращения) и может быть получен вращением параболы вокруг своей оси.

Рассмотрим уравнение гиперболического параболоида

где параметры p и q положительны. В сечении координатной плоскостью xOz поверхности, определяемой этим уравнением, получается «вос-

дящей» параболе, а каждая плоскость x h – по «нисходящей» параболе. В сечениях, параллельных координатной плоскости xOy , получаются ги-

перболы. Гиперболический параболоид обладает двумя плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями xOz и yOz ) и имеет вид «седла» (рис. 28.7).

Поверхность гиперболического параболоида можно также получить

скользящая парабола и образует гиперболический параболоид.

Рис. 28.7

207

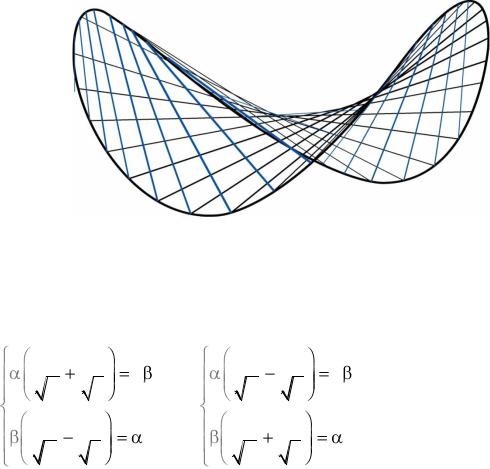
Интересно, что гиперболический параболоид, как и однополостный гиперболоид, является линейчатой поверхностью – его можно сформировать из прямых (рис. 28.8).

Рис. 28.8

Гиперболический параболоид с уравнением (28.6) имеет две системы прямолинейных образующих, определяемых уравнениями

208

Раздел 6. Математический анализ. Интегральное исчисление

Лекция 29. Неопределенный интеграл

Наряду с задачей дифференцирования функции, в которой для заданной функции f (x) требуется найти ее производную f ′(x), часто приходится решать обратную задачу, называемую интегрированием функции: для заданной функции f (x) найти такую функцию F(x), производная которой совпадает с функцией f (x) , т.е. F′(x) = f (x) . Например, предполагая, что известно уравнение движения S = S(t) , т.е. закон изменения пути с течением времени, можно найти скорость v(t) = S′(t). Если, напротив, задана скорость как функция времени v = v(t), то возникает задача об определении пройденного путиS в зависимости от времени, т.е. по функции v = v(t) «восстановить» функциюS(t), для которой v = v(t) является производной S′(t) = v(t). В данной лекции рассмотрим решение этой обратной задачи. Происхождение термина интегрирование связано с именем Я. Бернулли (1654-1705). Вероятно, он произвёл термин от латинского integro – приводить в прежнее состояние, восстанавливать.

29.1. Первообразная функция и неопределённый интеграл. Функция F(x) называется первообразной функции f (x) на промежутке (a,b), если для любого x (a,b) выполняется равенство

dF(x) = f (x). dx

К сожалению, это определение не даёт способа нахождения первообразной F(x)данной функции f (x) . Однако для основных элементарных функций эта задача разрешима, поскольку известны их производные. Например, легко видеть, чтопервообразнойфункции f (x) = cos xбудет функция F(x) = sin x ,так как (sinx)' = cosx. Но для функции f (x) = cos x есть и другие первообразные.Например, F(x) = sin x +1, F(x) = sin x + 2 и, вообще,F(x) = sin x + C , где C– любое число.

Из этого примера следует, что одна и та же функция имеет множество первообразных. Возникает вопрос – как найти всё это множество? Покажем, что множество функций F(x) + C , где F(x)– некоторая

209

первообразная функции f (x) , а C– произвольная постоянная, исчерпывает все первообразныефункции f (x) .

Теорема.Если F1(x) и F2 (x) – двепервообразные функции f (x) ,то F1(x) = F2 (x) + C, где C–некоторая постоянная.

Доказательство. Рассмотрим функциюϕ(x) = F1 (x) − F2 (x) . Так как для любого x имеем

ϕ′(x) = F1′(x) − F2′(x) = f (x) − f (x) = 0,

то по формуле Лагранжа конечных приращений получаем, что ϕ(x) ≡ C , и,

следовательно,F1 (x) − F2 (x) = C .

Таким образом, достаточно найти одну первообразную F(x) данной функции f (x) , чтобы знать всё множество её первообразных {F(x) + C} . Для обозначения рассматриваемой операции – нахождения функции F(x) из равенства

dF(x) = f (x)dx,

был введён символ ∫ , применение которого к указанному равенству восстанавливает множество всех первообразных данной функции f (x) (по-

добно тому, как знак обозначает операцию нахождения квадратного корня). Для краткости совокупность всех первообразных функции f (x) называется её неопределенным интегралом и обозначается так

∫ f (x)dx = F(x) + C,

где C –некоторая постоянная. Операция нахождения неопределенного интеграла называется интегрированием.При этом функция f (x)

называетсяподынтегральной функцией, f (x)dx –подынтегральным выражением,а знак ∫ – знаком интеграла.

Поставим вопрос: для всякой ли функции f (x) существует первообразная, а, следовательно, и неопределенный интеграл? Сформулируем без доказательства достаточное условие интегрируемости: если функция f (x) непрерывна на интервале(a,b),то на этом множестве у функции f (x) существует первообразная, а, значит, и неопределённый интеграл. Ниже будем говорить об интегралах непрерывных функций, которые заведомо существуют.

210