
10546
.pdf
частного двух функций равен сумме, разности, произведению, частному их пределов (в случае частного предел знаменателя должен быть отличен от нуля). Эти свойства используются для раскрытия неопределенностей при нахождении предела функции аналогично тому, как это делалось при нахождении пределов последовательностей.
17.2. Первый замечательный предел. Продемонстрируем в качестве примера нахождение так называемого первого замечательного предела
|
|
lim |
sin x |
=1.(17.1) |
|
|
|
|
|
||||
|
|
x→0 x |
||||
В данном случае мы имеем неопределенность вида |
0 |
. Поскольку |
||||
|
||||||
|
|
0 |
|
|||
функция |
f (x) = sin x |
– чётная и нас интересует её поведение при x → 0, |
||||
|
x |
|
|
|
|
|
то значение аргумента x, измеряемое в радианах, будем считать положительным и малым. Рассмотрим часть дуги окружности AFC единичного радиуса.
OA = OC = 1 |
A |
B |
AD = sin x |
|
|
DC = 1− cos x |
|
F |
|
|
|
x
O D C
Рис. 17.2
Площадь сегмента AFC меньше площади прямоугольника ABCD ,поэтому для них имеем неравенство:
0 < SAFC < SABCD .(17.2)
Площадь сегмента найдём как разность площадей сектора OAFC и треугольника OAC
1 1
SAFC = 2 x − 2sin x > 0.
121
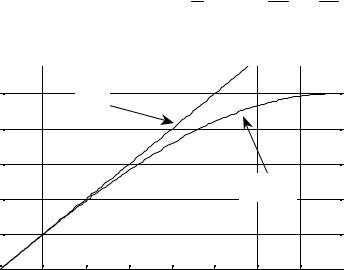
Отсюда следует неравенство sin x < x ( x > 0). Полезно представить его графическую иллюстрацию (см. рис. 17.3). Применим это неравенство для оценки площади прямоугольника ABCD
S |
ABCD |
= sin x(1− cos x) = 2sin2 x sin x < 2 x2 |
x = x3 |
||||||
|
|
|
|
|
2 |
4 |
|
2 |
|
|
|
|
|
|
|
|
|||
|
1 |
|
y=x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
y=sinx |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
Рис. 17.3
Тогда неравенство (17.2) примет вид
0 < |
1 |
x − |
1 |
sin x < |
x3 |
или |
0 < 1− |
sin x |
< x2 . |
||
|
|
|
|
|
|
||||||
2 |
|
2 |
2 |
|
|
x |
|||||
Когда x → 0, то 1− |
sin x |
|
|
→ 0, а это и означает (17.1). |
|||||||
|
|
|
|||||||||
x
Второй замечательный предел, когда аргумент принимает вещественные значения, имеет вид
|
|
1 x |
||
lim 1 |
+ |
|
|
= e. |
|
||||
x→+∞ |
|
x |
|
|
17.3. Непрерывность функции. Понятие предела функции позволяет сформулировать такое важное свойство функции как ее непрерывность в данной точке. Интуитивно ясно, что непрерывной зависимости соответствует ситуация, когда «малое» изменение аргумента вызывает «малое» изменение значения функции. Геометрически это означает, что график этой функции рисуется, не отрывая карандаша от бумаги, т.е. непрерывно. Математически это понятие определяется следующим образом.
122
Функция f (x) непрерывна в точке x0 , если эта точка вместе с некоторой ее окрестностью входит в область определения функции и
lim f (x) = f (x0 ). |
(17.3) |
x→x0 |
|
Фактически условие (17.3) означает, что |
|
lim f (x) = f (limx), |
|
x→x0 |
x→x0 |
т.е. при нахождении предела непрерывной функции знак предела и знак функции можно менять местами. Пример использования этого свойства непрерывной функции рассмотрим в связи с отысканием следующего предела
|
|
2 |
3n |
|
|
|
(−2) |
− |
n |
−6 |
|
|
|
(−2) |
− |
n |
−6 |
|
|
|||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
−6 |
|||||||||||
lim 1 |
− |
|
|
|
= lim 1 |
+ |
|
|
|
|
|
= lim 1 |
+ |
|
|
|
|
|
= e |
|
||
|
|
|
|
|
|
|
|
|
||||||||||||||
n→∞ |
|
n |
|
n→∞ |
|
n |
|
|
|
n→∞ |
|
n |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь мы поменяли местами порядок взятия предела и вычисления функции и применили второй замечательный предел.
Условие (17.3) также может быть записано в эквивалентном виде
lim [ f (x) − f (x0 )] = 0,
x−x0 →0
означающее, что приращение непрерывной функции f = f (x) − f (x0 )
стремится к нулю, когда приращение аргумента x = x − x0 стремится к нулю, т.е.
lim f = 0 .
x→0
Из определения следует, что для непрерывной в точке функции предел слева равен пределу справа и равен значению функции в этой точке
lim f (x) = lim f (x) = f (x0 ).(17.4)
x→x0 −0 x→x0 +0
Если нарушается хотя бы одно из этих равенств и оба односторонних предела существуют и конечны, то говорят, что в данной точке функция имеет разрыв первого рода. В остальных случаях нарушения условий непрерывности, т.е. когда хотя бы один из односторонних пределов не существует или равен бесконечности, у функции в этой точке разрыв второго
123
рода. Например, функция y = |
x |
|
непрерывна во всех точках области оп- |
| x |
|
||
|
| |
||
ределения, а в точке x0 = 0«терпит» разрыв первого рода.
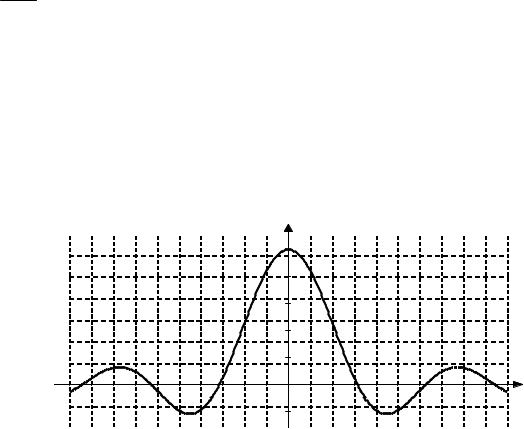
Отметим так называемый устранимый разрыв, когда односторонние пределы в точке конечны и равны, а в самой точке функция или не определена или ее значение не совпадает с односторонними пределами. В этом случае можно или доопределить или изменить значение функции в этой точке так, чтобы ее значение было равно односторонним пределам (17.4), тем самым получив непрерывную функцию. Например, функция
y = sin x не определена в точке x = 0. Учитывая первый замечательный |
|
x |
0 |
|
|
предел, доопределим её до непрерывной функции следующим образом:
sin x |
x ≠ 0 |
||
|
|
, |
|
|
|||
y = |
x |
|
|
|
1, |
|
x = 0 |
|
|
||
Это непрерывная в точке x |
= 0функция (см. рис. 17.4). |
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0.75 |
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0.25 |
|
|
|
|
|
|
|
|
|
X |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
|
|
|
-0.25 |
|
|
|
|
|
|
Рис. 17.4 |
|
|
|
17.4. Свойства непрерывных функций. Функция называется непрерывной в данном интервале, если она непрерывна во всех точках этого интервала. Все элементарные функции непрерывны в областях их определения. Соответствующие свойства предела функции позволяют утверждать, что сумма, произведение, частное (когда знаменатель не равен нулю) непрерывных функций есть непрерывная функция.
Покажем, что сложная функция, представляющая собой суперпозицию непрерывных функций, является непрерывной. Пусть y = f (u) и u = ϕ(x) – непрерывные функции своих аргументов. Тогда
124

lim f (ϕ(x)) = f (lim ϕ(x)) = f (ϕ(x0 )), |
|
x→x0 |
x→x0 |
т.е. сложная функция f (ϕ(x))– непрерывна.
Очевидно также, что обратная к непрерывной функции тоже непрерывна (напомним, что графики взаимно обратных функций симметричны относительно биссектрисы первого координатного угла).
Если непрерывная функция на концах замкнутого промежутка принимает значения разных знаков, то внутри этого промежутка найдется, по крайней мере, одна точка, в которой функция обращается в ноль (см. рис.17.5).
|
|
|
y = f (x) |
f (b) > 0 |
|
|
|
|
|
a |
|
|
|
|
x1 |
x |
2 |
x3 |
b |
f (a) < 0 |
|
|
||
|
|
|
|
|
|
Рис.17.5 |
|
|
|
Это свойство применяется для поиска решения уравнения f (x) = 0 в заданном промежутке. Обычно задают допустимую погрешность ε , с которой этот корень нужно вычислить. Это значит, что нужно найти такой промежуток [a,b], содержащий корень ξ ( f (ξ) = 0 ), что его длина b − a < ε.Предполагается, что вычисление значений функции f (x) проблемы не составляет. Рассмотрим метод поиска корня на примере уравнения
f (x) = x3 − 3x2 + 3 = 0.
Функция f (x) всюду непрерывна. То, что это уравнение имеет, по крайней мере, один корень, видно из следующего представления этой функции
f (x) = x3(1− |
3 |
+ |
3 |
) . |
|
|
|
|
|||
|
x x2 |
|
|||
При больших по абсолютной величине значениях x |
знак функции f (x) |
||||
определяется первым из множителей. Поэтому при |
x → −∞, f (x) < 0, а |
||||
при x → +∞ , f (x) < 0. Значит, график непрерывной функции, по крайней мере, один раз пересечёт ось абсцисс. Сделаем попытку графического решения уравнения, представив его следующим образом: x3 = 3(x2 −1) .
125
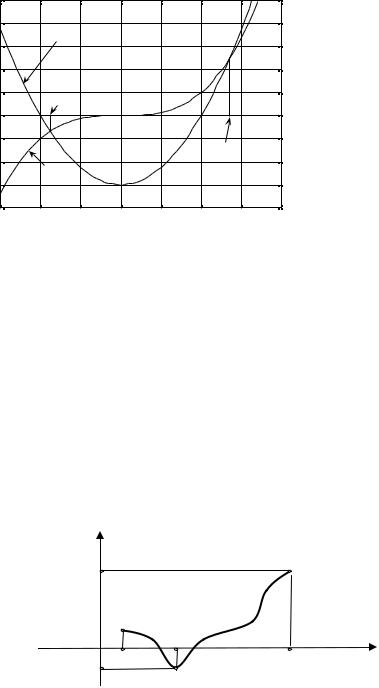
Видно, что в пределах чертежа обнаружились два корня, являющиеся |
|||||||
абсциссами точек пересечения графиков функций y = 3(x2 −1) и y = x3 (см. |
|||||||
рис.17.6). Так как y = x3 |
при |
|
x > 0 растет быстрее, чем y = 3(x2 −1) , то |
||||
графики этих функций пересекутся еще раз. Действительно, вычислив зна- |
|||||||
чения f (2) = −1< 0 |
и |
f (3) = 3> 0, убеждаемся, что этот корень нахо- |
|||||
дится в промежутке |
2 < x < 3. |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
4 |
y=3(x2-1) |
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
-1<x<0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
1<x<1.5 |
|
|
-2 |
|
|
|
|
|
|
|
|
y=x3 |
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
|
|
|
|
Рис.17.6 |
|
|
|
Вычислим с точностью до0,1корень уравнения из промежутка[1;1,5].Воспользуемся так называемым методом деления пополам. Под-
считаем значения функции в «средней» |
точке этого промежутка |
f (1,3) = 0,127 > 0и на одном из его концов |
f (1,5) = −0,375< 0. Следова- |
тельно, корень находится в промежутке1,3< x <1,5.Снова находя значение функции в средней точке f (1,4) = −0,136 < 0, убеждаемся, что корень находится в промежутке 1,3< x <1,4. Таким образом, поставленная задача решена. В дальнейшем мы познакомимся с более совершенными методами вычисления корней, где для достижения цели не требуется столь частого вычисления значений функции.
y
M
x1 x2
m a |
b |
Рис. 17.7
126
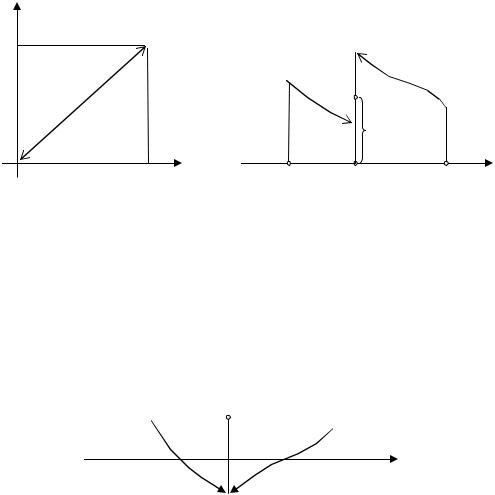
Непрерывная функция ограничена на замкнутом промежутке и принимает свои наименьшее и наибольшее значения в этом промежуткеm = f (x1) ≤ f (x) ≤ f (x2 ) = M .
Если функция определена на открытом промежутке, то она может быть неограниченной в этом промежутке. Например, функция f (x) =1/ x не ограничена в промежутке (0,1). В открытом промежутке функция, бу-
дучи даже ограниченной, может не иметь ни наименьшего, ни наибольшего значений. Например, функция f (x) = x в промежутке (0,1) (см. рис.
17.8a).
Если промежуток замкнут, но функция имеет разрыв в некоторой точке x0 , то функция может быть как неограниченной (в случае разрыва второго рода), так и может не иметь ни наименьшего, ни наибольшего значений в заданном замкнутом промежутке (см. рис. 17.8b).
y
1 |
|
|
|
|
|
|
f (x) = x |
|
|
|
|
a) |
|
|
b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x0 ) |
O |
1 |
x |
a |
x0 |
b |
|
|
|
Рис. 17.8 |
|
|
Если непрерывная функция положительна (отрицательна) в некоторой точке, то существует окрестность этой точки, в которой функция сохраняет знак.
На рис. 17.7 в точке x1 функция отрицательна и существует некоторая окрестность этой точки, в которой знак функции сохраняется. Для разрывной функции, как это видно из следующего рисунка, это не так.
x0 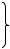 f (x0 )
f (x0 )
Рис. 17.9
Значение функции в точке x0 положительно, но в любой малой окрестности этой точки функция принимает только отрицательные значения.
127

Лекция 18. Производная
18.1. Физический, геометрический и математический смысл производной. Одним из основных понятий математического анализа является понятие производной функции. Прежде чем привести его математическое определение, рассмотрим несколько задач, приводящих к этому понятию.
Первая задача связана с определением мгновенной скорости движущейся точки. Пусть известен закон движения точки x(t), движущейся по прямой Ox. Если точка движется равномерно, т.е. за равные промежутки времени она проходит одинаковые расстояния, то ее скорость равна
v(t) = x(t) − x(0) = const . t
Если точка движется неравномерно, то что мы будем понимать под скоростью точки?
За |
промежуток времени |
[t,t + t]точка проходит расстояние |
x = x(t + |
t) − x(t) . Если величина |
t достаточно мала, то можно считать, |
что в этом промежутке точка движется равномерно и тогда приближенно ее скорость равна
v(t) ≈ x . t
Величинаv(t) тем ближе к скорости в момент времени t , чем меньше
t .Скоростью точки в момент времени t назовем предел этого отношения, когда длина интервала времени t стремится к нулю, т.е.
v(t) = lim |
x(t + |
t) − x(t) |
. |
|
|
||
t→0 |
t |
||
Вторая задача связана с понятием плотности массы тонкого неоднородного стержня. Пусть поперечное сечение стержня мало по сравнению с его длиной. Тогда плотность массыρ(x) этого стержня в точке с координатой xопределим как предел отношения массы m = m(x + x) − m(x) части стержня [x,x + x] к ее длине x, т.е.
ρ(x) = lim |
m(x + |
x)− m(x) |
. |
|
|
||
x→0 |
x |
||
128 |
|
|
|
Третья задача связана с проведением касательной прямой к заданной кривой.
|
y= f(x) |
|
|
|
M(x, y) |
|
|
|
y |
|
|
|
M0 |
|
|
|
x |
|
|
α0 |
α( x) |
|
|
|
Рис. 18.1 |
|
|
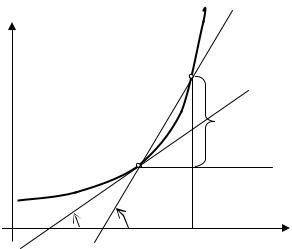
Под касательной к графику функции y = f (x)в точке |
M0 будем |
||
понимать предельное положение секущей M0M , когда точка |
M движет- |
||
ся вдоль кривой к точке M0 или, другими словами, |
x → 0(если это пре- |
||
дельное положение существует). Нормалью назовем |
прямую, проходя- |
||
щую через данную точку перпендикулярно касательной. Пусть касательная образует с положительным направлением оси Ox угол α0 , а секущая – α( x) . Тогда по определению
lim tgα( |
x) = lim |
y = tgα |
0 |
, |
x→0 |
x→0 |
x |
|
|
|
|
т.е. тангенс угла наклона касательной равен пределу отношения приращения функции к приращению аргумента.
Отвлечемся теперь от конкретных задач и для произвольной функции y = f (x)дадим аргументу x приращение x. Тогда функция получит приращение y = f (x + x) − f (x). Рассмотрим предел отношения приращения функции y к приращению аргумента x, когда приращение аргумента стремится к нулю, т.е.
lim y .
x→0 x
Если этот предел существует, то он называется производной функции f (x) в точке x и обозначается f ′(x).Поскольку производная в точке x является функцией x, то, чтобы подчеркнуть этот факт, пользуются терми-
129
ном производная функция ( f ′(x)– производная функция функции f (x) , кратко: f ′(x)– производная f (x) ).
Согласно этому определению скорость движения точки есть производная пути по времени v(t) = x′(t), плотность массы стержня – производная массы по координате ρ(x) = m′(x) , а тангенс угла α0 между положительным направлением оси Ox и касательной к графику функции в данной точке равен значению производной функции в этой точке f ′(x0 ) = tgα0 .
18.2. Вычисление производных. Операция нахождения производной функции называется дифференцированием. Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Пример недифференцируемой в точке x = 0 функции y =| x| приведен на рис. 18.2
|
|
|
|
y |
|
|
|
|
|
|
|
y = x |
|
|
y = −x |
|
|
|
||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Рис. 18.2 |
|
|
|
Действительно, для этой функции имеем |
|
|
||||
|
lim |
y =1 , |
lim |
y = −1 , |
|
|
|
x→+0 |
x |
x→−0 |
x |
|
|
а, значит, предел этого отношения не существует когда |
x → 0 произ- |
|||||
вольным образом.
Если производная в данной точке существует и конечна, т. е. отношения y к x стремится к конечной величине, когда x → 0, то отсюда следует, что y → 0. Таким образом, дифференцируемая в данной точке функция будет непрерывной в этой точке. Обратное утверждение не верно, как показывает приведенный выше пример (см. рис. 18.2). В точке x = 0 функция y =| x| непрерывна, но недифференцируема.
Итак, непрерывность функции в данной точке – необходимое условие её дифференцируемости. Другими словами, если функция дифференцируема в данной точке, то она непрерывна в этой точке. Ввиду важности этого утверждения приведём его формальное доказательство.
130
