9698

Таким образом, условия (39.2) выражают необходимые условия условного экстремума. Образовав функцию Лагранжа

F ( x, y, λ) = f ( x, y) + λ g ( x, y) ,

убеждаемся, что условия (39.2) совпадают с необходимыми условиями экстремума этой функции.

Пример. Найти экстремумы функции f (x, y) = x2 + y2 при условии,

что её аргументы связаны соотношением 5x2 − 6xy + 5 y2 − 32 = 0 . Образуем функцию Лагранжа

F (x, y,λ) = x2 + y2 + λ( 5x2 − 6xy + 5y2 − 32) .

Приравнивая к нулю её частные производные, получаем следующую систему для нахождения координат стационарных точек

Исключаем из первых двух уравнений параметр λ , разделив одно из них на другое

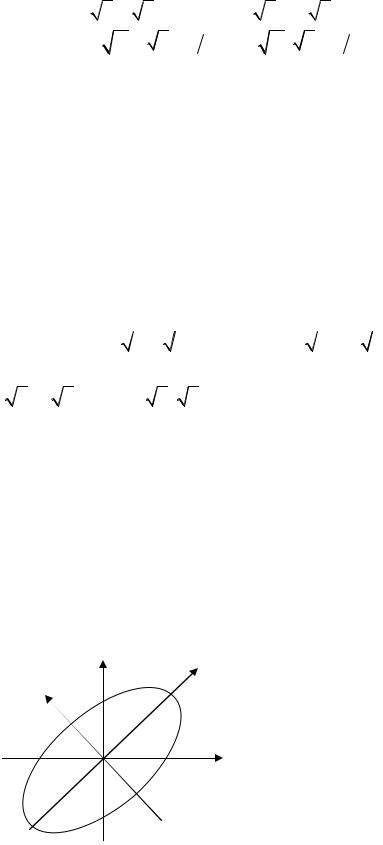
Откуда k = ±1 или y0 = ± x0 . Третье уравнение системы даёт возможность найти конкретные значения координат стационарных точек.

общем случае. Его исследование завело бы нас слишком далеко. Как и в случае безусловного экстремума, в практических приложениях обыкновенно заранее известно, что экстремум существует и каков его характер. Так, например, если на нашу задачу посмотреть с геометрической точки зрения (см. рис. 39.3), то мы находим на эллипсе

5x2 − 6xy + 5 y2 − 32 = 0

точки, наиболее удалённые от начала координат и наиболее близкие к нему, т.к. функция

f (x, y) = x2 + y2

Решая задачу на условный экстремум, мы «попутно» привели

Рис. 39.3

271