9698

называется общим уравнением линии (кривой) второго порядка. В нём

относится к классу уравнений второго порядка и получается из общего вида (25.1) при конкретном значении коэффициентов.

Простейшим примером кривой, задаваемой уравнением (25.1), является окружность. Окружность определяется как множество точек плоскости, равноудалённых от заданной точки (центра). Вводим на плоскости прямоугольную декартову систему координат, совместив её начало с центром окружности. Координаты произвольной точки M , лежащей на окружности, обозначим x и y . Эти координаты связаны

между собой равенством x2 + y2 = R2 , которое и представляет собой уравнение окружности. Ему удовлетворяют координаты каждой точки окружности и не удовлетворяют координаты любой другой точки плоскости, не лежащей на ней. Видим, что это уравнение является уравнением второго порядка.

К другим линиям, задаваемым уравнением (25.1), относятся эллипс, гипербола и парабола. В некоторых случаях получаются пара пересекающихся или параллельных прямых, одна прямая или точка. Изучение этих классических линий мы, как и для окружности, будем начинать с их определения. Дальше будем ставить задачу вывести уравнение, которому удовлетворяют координаты точек в том и только том случае, когда точки лежат на рассматриваемой линии. Для получения уравнения будем вводить систему координат, располагая её по отношению к линии так, чтобы уравнение в этой системе имело простейший вид,

называемый каноническим уравнением линии.

25.1. Эллипс. Эллипсом называется множество всех точек M плоскости, сумма расстояний каждой из которых до двух данных точек F1 и F2 есть величина постоянная (её принято обозначать 2a ). В этих обозначениях можно коротко записать определение эллипса в виде равенства MF1 + MF2 = 2a . Точки F1 и F2 называются фокусами эллипса. Расстояние F1F2 между фокусами обозначают 2c .

Из определения непосредственно вытекает способ построения: если концы нерастяжимой нити длины 2a закрепить в точкахF1 и F2 , затем натянуть нить остриём карандаша, то при движении острия оно будет вычерчивать выпуклую замкнутую линию (овал). Сумма расстояний от произвольной точки M до двух фиксированных точек F1 и F2 не может быть меньше расстояния между точками F1 и F2 : MF1 + MF2 ³ F1F2 . Будем предполагать, что это неравенство строгое, т.е. 2a > 2c или a > c .

170

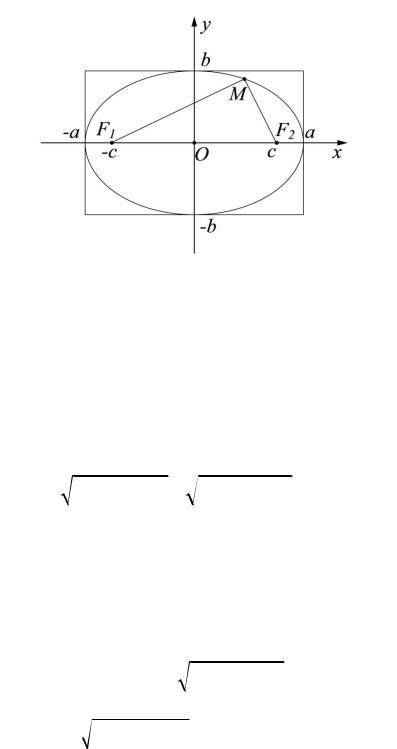
Выведем теперь уравнение эллипса. Для этого введём прямоугольную декартову систему координат. В качестве оси абсцисс мы возьмём прямую, проходящую через F1 и F2 , считая её направленной от F1 к F2 , начало системы координат поместим в середине отрезка F1F2 (рис. 25.1).

Рис. 25.1

В этой системе координат для произвольной точки M координаты обозначим через x и y . Фокусы, оказавшись теперь на оси Ox

симметрично относительно начала, будут иметь координаты F1 (−c;0) и

F2 (c;0) . Расстояния MF1 и MF2 между точками заменим их выражениями через координаты. Получим

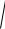( x + c )2 + y2 + 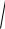( x − c )2 + y2 = 2a .

По существу, это соотношение представляет собой уравнение эллипса. Ему удовлетворяют координаты точек в том и только том случае, когда точки лежат на эллипсе. Проведём алгебраические преобразования, упрощающие эту запись. Для этого уединим в уравнении первый радикал, возведём в квадрат обе части полученного равенства

( x + c )2 + y2 = 4a2 − 4a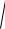( x − c )2 + y2 + ( x − c )2 + y2

и приведём его к виду a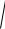( x − c )2 + y2 = a2 − cx . Возведя в квадрат обе части последнего равенства, найдём

(a2 − c2 ) x2 + a2 y2 = a2 (a2 − c2 ) .

171

Мы отмечали, что a > c , значит a2 − c2 > 0 , и можно ввести в рассмотрение

новую величину b = 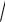a2 − c2 (при этом b < a ). Тогда уравнению можно придать вид b2 x2 + a2 y2 = a2b2 или

чётных степенях, поэтому если точка ( x, y ) принадлежит эллипсу, то ему принадлежат и точки ( x;− y ), (−x; y ), (− x, − y ). Отсюда следует, что эллипс симметричен относительно осей Ox и Oy , также относительно начала координат. Оси симметрии эллипса называются его осями, а точка пересечения осей – центром эллипса. Точки, в которых эллипс пересекает свои оси, называются его вершинами. Положив y = 0 в уравнении (25.2),

уравнения, можно теперь непосредственно построить в первой четверти

относительно осей координат, получить овальную замкнутую кривую, изображённую на рисунке 25.1. Отметим, что при этом все точки эллипса лежат внутри прямоугольника, образованного прямыми x = a , x = −a ,

эксцентриситет определяется соотношением осей эллипса. В случае ε = 0 (если a = b ) эллипс превращается в окружность с уравнением x2 + y2 = a2 .

172

Чем ближе эксцентриситет к единице, тем меньше отношение b и тем a

больше эллипс вытянут.

25.2. Гипербола. Множество всех точек M плоскости, разность расстояний которых до двух данных точек F1 и F2 есть величина постоянная, называется гиперболой. Указанная разность берётся по абсолютному значению и обозначается 2a . Точки F1 и F2 называются

находится ближе к фокусу F1 , то MF2 − MF1 = 2a . Из рассмотрения суммы

соответственно: F1 (−c;0), F2 (c;0) . Заменив расстояние MF1 и MF2 между точками их выражениями через координаты, получим

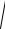( x + c )2 + y 2 − 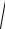( x − c )2 + y 2 = ±2a .

После преобразований, аналогичных тем, которые были проделаны для уравнения эллипса, соотношение приобретает вид

xc − a2 = ±a( x − c )2 + y2 .

Возведя в квадрат и упростив, получим (c2 − a2 ) x2 − a2 y2 = a2 (c2 − a2 ) .

гипербола симметрична относительно осей Ox и Oy , а также относительно начала координат. Оси симметрии гиперболы называются её осями, а точка пересечения осей – центром гиперболы. Положив y = 0 в уравнении (25.3), найдём две точки пересечения гиперболы с осью Ox : A1 (-a;0) , A2 (a;0) , которые называются вершинами гиперболы. Если

взять x = 0 в уравнении (25.3), то получим y2 = -b2 . Следовательно, с осью Oy гипербола не пересекается. Отрезок A1 A2 = 2a принято называть

называется мнимой осью ( ОB1 = b – мнимой полуосью). Прямоугольник со сторонами 2a и 2b называется основным прямоугольником гиперболы (рис. 25.3).

Тем самым приходим к заключению: если y > 0 , то точка M ( x, y ) при возрастании x , начиная от x = a , движется всё время «вправо» и «вверх»; если y < 0 , то M ( x, y ) движется «вправо» и «вниз». Так образуется

неограниченная правая ветвь. При x → −∞ от значения x = −a получается левая неограниченная ветвь гиперболы (рис. 25.2).

174

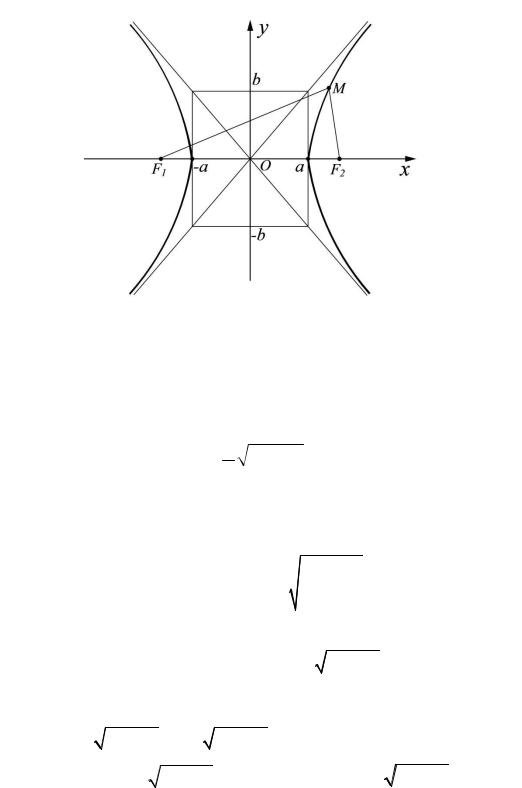
Рис. 25.2

Присмотримся более внимательно к тому, как именно точка M «уходит в бесконечность». В лекциях по математическому анализу было введено понятие наклонной асимптоты графика функции. Из уравнения

(25.3) выразим переменную y = ± b x2 − a2 . Далее для полученных двух a

Итак, построение гиперболы по каноническому уравнению (25.3) следует начинать с изображения основного прямоугольника, продолжая диагонали которого мы получим асимптоты. Обе бесконечные ветви

175

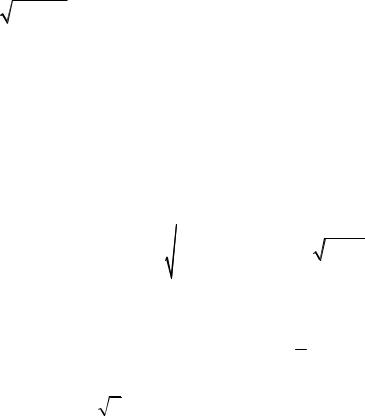
рисуем неограниченно приближающимися к ним (рис. 25.2). Фокусы

прямоугольник равносторонней гиперболы становится квадратом; прямые y = x и y = − x являются асимптотами, перпендикулярными друг к другу.

Отношение расстояния между фокусами к расстоянию между вершинами гиперболы называется эксцентриситетом гиперболы и

Следовательно, как и для эллипса, эксцентриситет гиперболы определяется отношением её осей. Он характеризует форму основного прямоугольника

гиперболы. Чем меньше эксцентриситет, тем меньше отношение b , то есть a

основной прямоугольник более вытянут в направлении действительной оси. Для равносторонней гиперболы ε = 2 .

Лекция 26. Парабола. Приведение кривых к каноническому виду

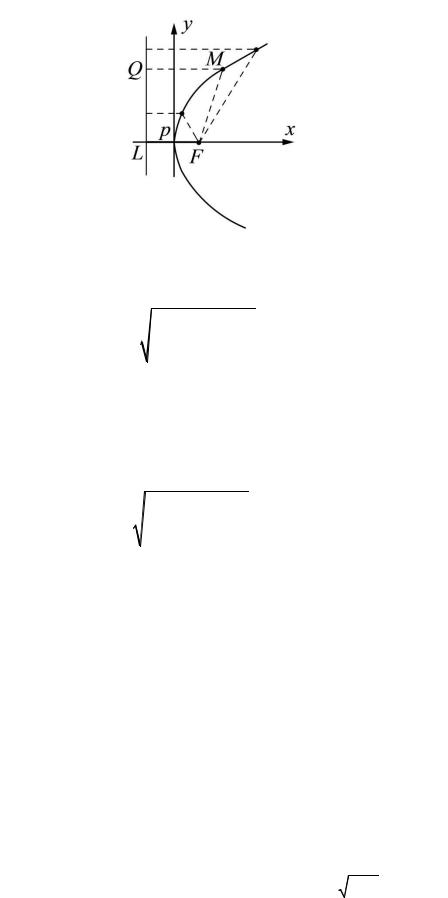
26.1. Парабола. Множество всех точек плоскости, равноудалённых от данной точки F (фокуса) и данной прямой L (директрисы), называется параболой. Расстояние от фокуса до директрисы параболы принято обозначать через p (рис. 26.1). Величину p называют фокальным параметром параболы.

Для получения уравнения параболы необходимо ввести систему координат на плоскости. Проведём ось абсцисс через фокус параболы перпендикулярно директрисе, будем считать её направленной от директрисы к фокусу; начало координат расположим посередине между

176

Возведя обе части равенства в квадрат получим каноническое уравнение

параболы

что доказывает симметрию параболы относительно оси Ox . Так как p > 0 , то переменная x должна быть неотрицательной. Это означает, что

симметрично относительно оси Ox , получим геометрическое изображение параболы (рис. 26.1). Ось симметрии параболы (в данном случае

177

совпадающая с осью Ox ) называется её осью. Точка, в которой парабола пересекает свою ось, называется её вершиной (в нашем случае вершина совпадает с началом координат). Для описания геометрического смысла фокального параметра p можно взять какое-либо значение абсциссы, например, x = 1. Из уравнения (26.1) найдём соответствующие ему значения ординаты: y = ±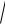2 p . Это даёт на параболе две точки M1 (1; 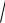2 p )

и M 2 (1;−2 p ), расстояние между которыми равно 22 p . Тем самым, чем больше p , тем больше расстояние M1M 2 . Следовательно, параметр p характеризует «ширину» области, ограниченной параболой.

Кроме рассмотренных классических кривых, уравнение линии второго порядка может привести ещё к нескольким геометрическим случаям, называемым вырожденными.

26.2. Вырожденные случаи. Если в уравнении линии второго порядка

коэффициенты B = D = E = F = 0 , то остаётся только два слагаемых, т.е. Ax2 + Cy2 = 0 . При одинаковых знаках A и C уравнению соответствует на

каноническому виду. Мы рассмотрели все геометрические ситуации, к которым может привести общее уравнение линии второго порядка (п. 26.2). В задачах аналитической геометрии обычно задаётся вид уравнения второго порядка с конкретными числовыми коэффициентами. В нём могут

что в исходной системе координат уравнение не является каноническим. Нужно перейти к другой системе координат, в которой уравнение будет иметь канонический вид. Это даст возможность определить, к какому из

178

рассмотренных случаев относится заданное уравнение. После этого легко будет построить график заданной кривой.

Для приведения уравнения линии второго порядка к каноническому виду используются только те преобразования системы координат, которые не изменяют расстояния между точками, то есть не деформируют кривую. К таким преобразованиям, в частности, относятся параллельный перенос и поворот осей координат. Этих преобразований достаточно для решения поставленных в этой лекции задач. Разберём далее, что происходит с уравнениями при том или ином преобразовании координат.

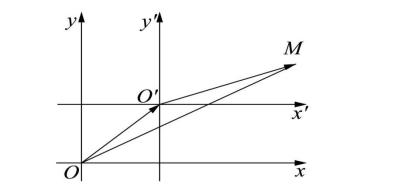
26.4. Параллельный перенос осей координат. Рассмотрим на

одинаково с ними направив. Масштаб сохраняем. Такой переход от системы xO y к системе Oўxўyў называется параллельным переносом осей координат.

Рис. 26.2

Для произвольной точки M координаты относительно исходных осей обозначим через (x; y), а координаты по отношению к «новым» осям

179