
- •Электричество и постоянный ток Электронный учебник по физике кгту-кхти. Кафедра физики. Старостина и.А., Кондратьева о.И., Бурдова е.В.
- •Оглавление
- •Электричество и постоянный ток
- •1. Электростатика.
- •1.1. Электрические заряды. Закон сохранения электрического заряда.
- •1.2. Закон Кулона.
- •1. 3. Электростатическое поле и его напряженность.
- •1.4. Графическое изображение электростатических полей
- •1. 5. Принцип суперпозиции электростатических полей.
- •1.6. Электростатическое поле электрического диполя.
- •1.7. Поток вектора напряженности электростатического поля
- •1. 8. Теорема Гаусса для электростатического поля в вакууме.
- •1. 9. Применение теоремы Гаусса для расчета напряженности электростатического поля.
- •1 Рис.1.12. К определению работы перемещения заряда в электростатическом поле. .10. Работа сил электростатического поля при перемещении заряда.
- •1.11. Циркуляция вектора напряженности электростатического поля.
- •1.12. Потенциальная энергия и потенциал электростатического поля.
- •1.13. Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.
- •1.14. Вычисление разности потенциалов по напряженности поля
- •1.15. Диэлектрики в электрическом поле
- •1.15.1. Типы диэлектриков. Поляризация диэлектриков.
- •1.15.2. Вектор поляризации и диэлектрическая восприимчивость диэлектриков
- •1.15.3. Напряженность поля в диэлектрике
- •1.15.4. Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике
- •1.15.5. Сегнетоэлектрики
- •1.15.6. Пьезоэлектрический эффект.
- •1. 16. Проводники в электростатическом поле
- •1. 17. Электрическая емкость уединенного проводника
- •1. 18. Взаимная электроемкость. Конденсаторы
- •1. 19. Энергия заряженного уединенного проводника, конденсатора. Энергия электростатического поля
- •2. Постоянный электрический ток
- •2.1. Электрический ток, сила и плотность тока
- •2.2. Сторонние силы. Электродвижущая сила и напряжение
- •2.3. Закон Ома для участка и полной замкнутой цепи
- •2.4. Сопротивление проводника. Явление сверхпроводимости.
- •2.5. Работа и мощность тока. Закон Джоуля-Ленца.
- •2. 6. Правила Кирхгофа для разветвленных цепей.
- •3. Электрические токи в металлах, вакууме и полупроводниках
- •3.1. Опытные доказательства электронной проводимости металлов.
- •3.2. Основные положения классической теории электропроводности металлов
- •3. 3. Работа выхода электрона из металла. Контактная разность потенциалов.
- •3. 4. Термоэлектрические явления
- •3. 5. Электрический ток в вакуумном диоде
- •3. 6. Собственная и примесная проводимость полупроводников.
- •3.7. Элементы современной квантовой или зонной теории твердых тел.
1. 8. Теорема Гаусса для электростатического поля в вакууме.
Рис.1.7.
К выводу теоремы Гаусса.

Рассмотрим сначала случай сферической поверхности радиусом R, окружающей один заряд +q, находящийся в ее центре (рис.1.7).
![]() ,
где
,
где
![]() -
есть интеграл по замкнутой поверхности
сферы. Во всех точках сферы модуль
вектора
-
есть интеграл по замкнутой поверхности
сферы. Во всех точках сферы модуль
вектора![]() одинаков, а сам он направлен перпендикулярно
поверхности. Следовательно
одинаков, а сам он направлен перпендикулярно
поверхности. Следовательно![]() .
Площадь поверхности сферы равна
.
Площадь поверхности сферы равна![]() .
Отсюда следует, что
.
Отсюда следует, что
 .
.
П
Рис.1.8. Пересечение
силовыми линиями поверхности, охватывающей
заряд (показано в сечении).

На рисунке 1.8 представлена произвольная замкнутая поверхность, охватывающая заряд q0. Некоторые линии напряженности то выходят из поверхности, то входят в нее. Для всех линий напряженности число пересечений с поверхностью является нечетным.
Как отмечалось в предыдущем параграфе, линии напряженности, выходящие из объема, ограниченного замкнутой поверхностью, создают положительный поток Фе; линии же, входящие в объем, создают отрицательный поток -Фе. Потоки линий при входе и выходе компенсируются. Таким образом, при расчете суммарного потока через всю поверхность следует учитывать лишь одно (не скомпенсированное) пересечение замкнутой поверхности каждой линией напряженности.
Если
заряд q
не охватывается замкнутой поверхностью
S,
то количество силовых линий, входящих
в данную поверхность и выходящих из
нее, одинаково (рис.1.9). Суммарный поток
вектора
![]() через такую поверхность равен нулю:
ФЕ=0.
через такую поверхность равен нулю:
ФЕ=0.
Р
Рис.1.9. Пересечение
силовыми линиями поверхности, не
охватывающей заряд (показано в сечении).

![]() ,
создаваемая зарядамиq1,q2,...qn
равна векторной сумме напряженностей,
создаваемых каждым зарядом в
отдельности:
,
создаваемая зарядамиq1,q2,...qn
равна векторной сумме напряженностей,
создаваемых каждым зарядом в
отдельности:
 .
Проекция вектора
.
Проекция вектора![]() - результирующей напряженности поля
на направление нормали к площадкеdS
равна алгебраической сумме проекций
всех векторов
- результирующей напряженности поля
на направление нормали к площадкеdS
равна алгебраической сумме проекций
всех векторов
![]() на это направление:
на это направление: ,
,
отсюда
 .
.
Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную 0. Эта формулировка представляет собой теорему К.Гаусса.
В
общем случае электрические заряды могут
быть распределены с некоторой объемной
плотностью
![]() ,
различной в разных местах пространства.
Тогда суммарный заряд объемаV,
охватываемого замкнутой поверхностью
S
равен
,
различной в разных местах пространства.
Тогда суммарный заряд объемаV,
охватываемого замкнутой поверхностью
S
равен
![]() и теорему Гаусса следует записать в
виде
и теорему Гаусса следует записать в
виде![]() .
.
Теорема Гаусса представляет значительный практический интерес: с ее помощью можно определить напряженности полей, создаваемых заряженными телами различной формы.
1. 9. Применение теоремы Гаусса для расчета напряженности электростатического поля.
Поле равномерно заряженной бесконечной плоскости с поверхностной плотностью зарядов +.
Пусть
поверхностная плотность зарядов или
заряд, приходящийся на единицу поверхности
![]() .
Силовые линии поля перпендикулярны
этой плоскости и направлены от нее в
обе стороны (рис.1.10).
.
Силовые линии поля перпендикулярны
этой плоскости и направлены от нее в
обе стороны (рис.1.10).
Построим
замкнутую цилиндрическую поверхность
с основаниями dS,
параллельными заряженной поверхности
и образующей, параллельной вектору
![]() .
Следуя последнему условию, поток
напряженности ФЕ
через боковую поверхность цилиндра
равен нулю. Поэтому полный поток через
цилиндрическую поверхность равен
сумме потоков сквозь его основания. Так
как вектор
.
Следуя последнему условию, поток
напряженности ФЕ
через боковую поверхность цилиндра
равен нулю. Поэтому полный поток через
цилиндрическую поверхность равен
сумме потоков сквозь его основания. Так
как вектор
![]() перпендикулярен основаниям, Еn=Е
и суммарный поток ФЕ
можно записать ФЕ=2ЕdS.
перпендикулярен основаниям, Еn=Е
и суммарный поток ФЕ
можно записать ФЕ=2ЕdS.
Рис.1.10.
Определение напряженности поля
бесконечной заряженной плоскости.

 ,
где
,
где![]() - заряд, охватываемый цилиндрической
поверхностью. Таким образом
- заряд, охватываемый цилиндрической
поверхностью. Таким образом
![]() ,
,
![]() .
.
Если
плоскость помещена в среду с относительной
диэлектрической проницаемостью ,
то напряженность электростатического
поля, создаваемая плоскостью, равна
![]() .
.
Из формулы следует, что Е не зависит от расстояния между плоскостью и точкой наблюдения, т.е. поле равномерно заряженной бесконечной плоскости однородно.
Поле двух бесконечных разноименно заряженных плоскостей.
Рис.1.11.
Определение напряженности поля двух
параллельных разноименно заряженных
плоскостей.
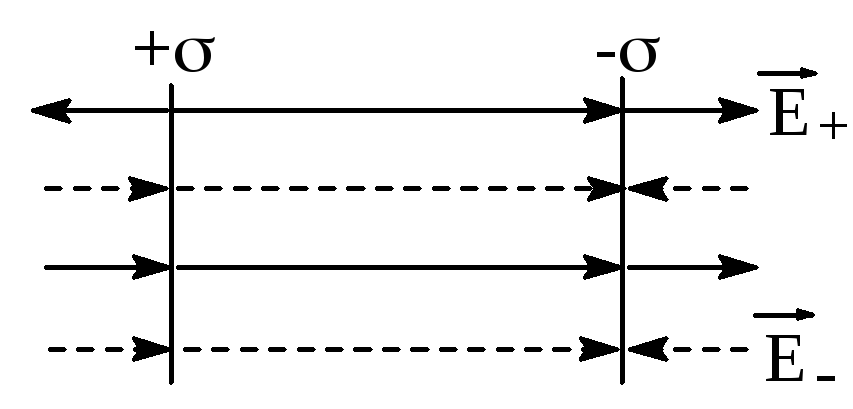
Напряженности
полей обеих плоскостей равны по абсолютной
величине
![]() .
Однако, справа и слева от плоскостей
напряженности
.
Однако, справа и слева от плоскостей
напряженности![]() и
и![]() направлены противоположно, поэтому
суммарная Е=0
и поле отсутствует. В области между
плоскостями
направлены противоположно, поэтому
суммарная Е=0
и поле отсутствует. В области между
плоскостями
![]() и
и![]() направлены одинаково, поэтому
направлены одинаково, поэтому![]() .
.
