1. 17. Электрическая емкость уединенного проводника

Уединенным называется проводник, вблизи которого нет других заряжен­ных тел, диэлектриков, которые могли бы повлиять на распределение зарядов дан­ного проводника.

Отношение величины заряда к потенциалу для конкретного проводника есть величина постоянная, называемая электроемкостью (емкостью) С , .

Таким образом, электроемкость уединенного проводника численно равна заряду, который необходимо сообщить проводнику, чтобы изменить его потен­циал на единицу. Опыт показал, что электроемкость уединенного проводника зависит от его гео­метрических размеров, формы, диэлектрических свойств окружающей среды и не за­висит от величины заряда проводника.

Рассмотрим уединенный шар радиуса R, находящийся в однородной среде с диэлектрической проницаемостью . Ранее было получено, что потенциал шара ра­вен . Тогда емкость шара, т.е. зависит только от его ра­диуса.

За единицу емкости принимается 1фарад (Ф). 1Ф - емкость такого уединенно­го проводника, потенциал которого изменится на 1В при сообщении заряда 1Кл. Фарад - очень большая величина, поэтому на практике используют дольные едини­цы : милли­фарад (мФ, 1мФ=10^-3Ф), микрофарад (мкФ, 1мкФ=10^-6Ф), нанофарад (нФ, 1нФ=10^-9Ф), пикофарад (пФ, 1пФ=10^-12Ф).

Уединенные проводники даже очень больших размеров обладают малыми ем­костями. Емкостью в 1Ф обладал бы уединенный шар радиуса, в 1500 раз большего радиуса Земли. Электроемкость Земли составляет 0.7 мФ.

1. 18. Взаимная электроемкость. Конденсаторы

Пусть вблизи заряженного проводника А нахо­дятся незаряженные проводни­ки или диэлектрики. Под действием поля проводника А в телах 1 и 2 возни­кают индуцированные (если 1 и 2 проводники) или свя­занные (если диэлектрики) заряды, причем ближе к А будут располагаться заряды противоположного знака (рис.1.25). Индуцированные (или связанные) заряды соз­дают свое поле противоположного на­правления, чем ослабляют поле проводника А, уменьшая его потенциал и увеличи­вая его электроемкость.

Рис.1.25. Взаимное влияние проводников.

На практике существует потребность в устройствах, которые при относитель­но небольшом потенциале накапливали (конденсировали) бы на себе заметные по вели­чине заряды. В основу таких устройств, называемыхконденсаторами, поло­жен факт, что емкость проводника возрастает при приближении к нему других тел. Простейший плоский конденсатор состоит из двух близко расположенных про­водников, заряженных равными по величине и противоположными по знаку заряда­ми. Образующие данную систему проводники называются обкладка­ми.

Для того, чтобы поле, создаваемое заряженны­ми обкладками, было полностью сосредоточено внутри конденсатора, обкладки должны быть в виде двух близко рас­положенных пластин, или коаксиаль­ных цилиндров, или концентрических сфер. Со­ответ­ственно конденсаторы называются плоскими, цилиндрическими или сфериче­скими.

Разность потенциалов между обкладками пропорциональна абсолютной вели­чине заряда обкладки. Поэтому отношение есть величина постоянная для конкретного кон­денсатора. Она обозначаетсяС и называется взаимной электроемкостью провод­ников или емкостью конденсатора. Емкость конденсатора численно равна заряду, который нужно перенести с одной обкладки конденсатора на другую, чтобы изме­нить разность их потенциалов на единицу.

Разность потенциалов плоского конденсатора равна , гдеповерхностная плотность заряда обкладки.S - площадь обкладки конденса­тора.. Отсюда емкость плоского конденсатора .Из этой формулы следует, что С плоского конденсатора зави­сит от его геометрических размеров, т.е. от S и d, и диэлектри­ческой проницаемости диэлектрика, заполняющего межплоско­стное пространство. Применение в качестве прослойки сегнетоэлектриков значительно увеличива­ет емкость конденсатора, т.к.  у них достигает очень больших значений. В очень сильных полях (порядка Е_пр10⁷ В/м) происходит разруше­ние диэлектрика или «пробой», он перестает быть изо­ля­тором и становится проводником. Это «пробивное напряжение» зависит от формы обкладок, свойств диэлектрика и его толщины..

Для получения устройств различной электроемкости конденсаторы соединяют парал­лельно и после­довательно.

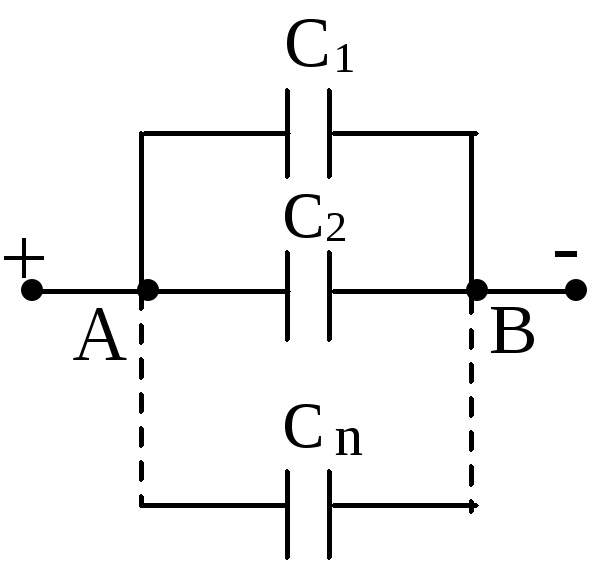
Параллельное соединение конденсаторов (Рис. 1. 26). В данном случае, так как соединенные провода-проводники имеют один и тот же потенциал, то разность потенциалов на обкладках всех конденсаторов оди­накова и равна . Заряды конденсаторов будут

, … , .

Рис.1.26.   Параллельное соединение конденса­торов.

Заряд, запасенный всей батареей .

Отсюда видно, что полная емкость системы из параллельно соединенных конденсаторов равнасумме емкостей всех конденсаторов.

Последовательное соединение конденсаторов (Рис. 1. 27). В данном случае, вследствие электростатической индукции, заряды на всех обкладок q будут равны по мо­дулю, а общая разность потенциалов складывается из разностей на отдельных конденсаторах . Так как, то. Отсюда.

Рис.1.27. Последовательное соеди­нение конденса­то­ров.

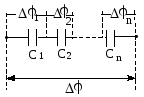
При последовательном сое­динении конденсаторов обратная величина результирующей емкости равна сумме обратных величин емкостей всех конденсаторов.