Основное уравнение молекулярно-кинетической теории идеального газа

Основное уравнение молекулярно-кинетической теории идеального газаустанавливает связь между макроскопической величиной - давлением, которое может быть измерено, например манометром, и микроскопическими величинами, характеризующими молекулу:

где р - давление, m₀- масса молекулы, п - концентрация (число молекул в единице объема), v²- средний квадрат скорости молекул.

Если через Е обозначить среднюю кинетическую энергию поступательного движения молекулы

можно записать:

Давление идеального газа пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.

уравнение состояния идеального газа (его также называют уравнением Клапейрона-Менделеева):

PV = nRT

где n – число молей газа;

P – давление газа (например, в атм;

V – объем газа (в литрах);

T – температура газа (в кельвинах);

R – газовая постоянная (0,0821 л·атм/моль·K).

ИЗОПРОЦЕССЫ

Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется.

ИЗОБАРНЫЙ ПРОЦЕСС- термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа. () Для изобарного процесса в идеальном газе справедлив закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его термодинамической температуре:или .   Работа газа при изобарном расширении: . Изменение внутренней энергии:Количество полученного тепла в соответствии с первым началом термодинамики:. Молярная теплоемкость при изобарном процессе:.

ИЗОХОРНЫЙ ПРОЦЕСС ()-термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. Изохорный процесс в идеальном газе описывается законом Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его термодинамической температуре: или .   Работа газа при изохорном процессе равна нулю: . Все полученное тепло идет на изменение внутренней энергии в соответствии с первым началом термодинамики: . Молярная теплоемкость при изохорном процессе:.

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС ()-термодинамический процесс, происходящий в физической системе при постоянной температуре. Изотермический процесс в идеальном газе подчиняется закону Бойля - Мариотта: для данной массы газа при неизменной температуре произведение значений давления и объема есть величина постоянная: или .

Работа газа при изотермическом расширении: 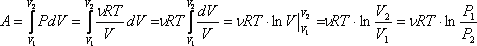. Изменение внутренней энергии при изотермическом процессе равно нулю:. Все полученное тепло идет на совершение работы в соответствии с первым началом термодинамики:.

13. Основное уравнение МКТ. Статистическое толкование температуры. Барометрическая формула. Распределения Максвелла и Больцмана.

Основное уравнение мкт имеет вид

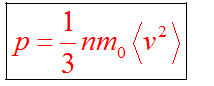
Определение температуры в статистической физике в статистической физике температура определяется как производная от энергии системы по её энтропии:

,

где S — энтропия, E — энергия термодинамической системы. Введённая таким образом величина T является одинаковой для различных тел при термодинамическом равновесии. При контакте двух тел тело с большим значением T будет отдавать энергию другому.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёмаускорение свободного падения одинаково), барометрическая формула имеет следующий вид:

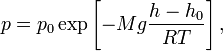
где — давление газа в слое, расположенном на высоте,— давление на нулевом уровне (),—молярная масса газа, —газовая постоянная, —абсолютная температура. Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону:

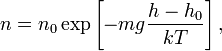
где — масса молекулы газа,—постоянная Больцмана.

Данное выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты, или высоту, если известно давление.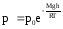

Закон Больцмана о распределении частиц во внешнем потенциальном поле.

Если воспользоваться выражением р = nkT, то можно привести барометрическую формулу к виду:

здесь n – концентрация молекул на высоте h, n₀ – то же у поверхности Земли. Так как М = m₀N_A , где m₀ – масса одной молекулы, а R = k N_A, то мы получим П = m₀gh – это потенциальная энергия одной молекулы в поле тяготения. Поскольку kT~‹ε_пост›, то концентрация молекул на определенной высоте зависит от соотношения П и ‹ε_пост›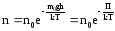

Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа (с которой связана концентрация) больше там, где меньше потенциальная энергия его молекул.