
- •Механика и молекулярная физика
- •Преобразования Галилея и механический принцип относительности.
- •Основное уравнение молекулярно-кинетической теории идеального газа
- •Определение температуры в статистической физике в статистической физике температура определяется как производная от энергии системы по её энтропии:
- •Распределение Максвелла молекул идеального газа по скоростям.
Механика и молекулярная физика
Вектор перемещения. Скорость и ускорение материальной точки. Нормальные и тангенциальные ускорения. Радиус кривизны траектории.
Пусть
за время
 материальная точка переместилась
из положения А в В по криволинейной
траектории (рис.3.1). Расстояние,
пройденное точкой вдоль траектории
за время
материальная точка переместилась
из положения А в В по криволинейной
траектории (рис.3.1). Расстояние,
пройденное точкой вдоль траектории
за время есть скалярная, положительная
величина – путь
есть скалярная, положительная
величина – путь .
. - радиусы-векторы точек А и В.
- радиусы-векторы точек А и В.
Вектор, соединяющий
точки А и В, называется вектором
перемещения
 ,
, . В общем случае модуль вектора перемещения
не равен пути (см. рис.3.1)
. В общем случае модуль вектора перемещения
не равен пути (см. рис.3.1) . Лишь при прямолинейном движении
. Лишь при прямолинейном движении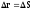 . На малых временных интервалах, когда
. На малых временных интервалах, когда ,
можно с большой точностью считать, что
,
можно с большой точностью считать, что .
.

Рис.3.1. Путь и перемещение точки.
Векторная физическая величина, характеризующая изменение радиус-вектора с течением времени, называется скоростью.
Векторная
физическая величина, характеризующая
изменение вектора скорости с течением
времени называется ускорением
 .
Различают среднее и мгновенное ускорения.
Среднее ускорение
.
Различают среднее и мгновенное ускорения.
Среднее ускорение
 равно отношению изменения вектора
скорости за времяt
к этому промежутку времени
равно отношению изменения вектора
скорости за времяt
к этому промежутку времени
 .
Мгновенное ускорение
.
Мгновенное ускорение ,
т.е. ускорение в данный момент времени
находится как предел
,
т.е. ускорение в данный момент времени
находится как предел приt
0.
Отсюда
приt
0.
Отсюда  =
= .
.
Вектор ускорения в данный момент времени определяется как первая производная от вектора скорости по времени или вторая производная от радиуса-вектора по времени.
Поскольку скорость
величина векторная, она может изменяться
как по величине, так и по направлению.
Изменение вектора скорости
 можно представить в виде суммы двух
слагаемых векторов
можно представить в виде суммы двух
слагаемых векторов и
и т.е.
т.е. =
= +
+ ,
где
,
где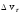 -
изменение скорости по величине,
-
изменение скорости по величине, -
изменение скорости по направлению
за промежуток времениt.
Поэтому вводят две составляющие
ускорения:
-
изменение скорости по направлению
за промежуток времениt.
Поэтому вводят две составляющие
ускорения:
 -
тангенциальное или касательное ускорение,
-
тангенциальное или касательное ускорение,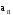 -
нормальное ускорение.Полное
ускорение
-
нормальное ускорение.Полное
ускорение
 , где
, где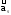 -
характеризует изменение скорости только
по величине, а
-
характеризует изменение скорости только
по величине, а -
характеризует изменение скорости
только по направлению.
На основании вышеизложенного можно
записать мгновенное ускорение
-
характеризует изменение скорости
только по направлению.
На основании вышеизложенного можно
записать мгновенное ускорение
 Рис.
4.1. Нормальное, тангенцальное и полное
ускорения.
Рис.
4.1. Нормальное, тангенцальное и полное
ускорения.
 ,
,

Тангенциальное
ускорение
 численно равно первой производной от
скорости по времени и направлено по
касательной к траектории в данной точке.
Вот почему
численно равно первой производной от
скорости по времени и направлено по
касательной к траектории в данной точке.
Вот почему
 называется еще касательным ускорением.
называется еще касательным ускорением.
Законы динамики материальной точки и системы точек. Внешние и внутренние силы. Центр масс. Динамика механической системы.
Первый закон
Ньютона: Если на материальную точку не
действуют силы или приложенные силы
взаимноуравновешены (т.е. суммарная
или результирующая сила равна нулю), то
материальная точка будет находиться
в состоянии покоя ( =0)
или равномерного прямолинейного
движения (
=0)
или равномерного прямолинейного
движения ( =const).
=const).
Второй закон Ньютона (основной закон динамики поступательного движения) - ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

Третий закон Ньютона. При взаимодействии две материальные точки действуют друг на друга с силами, равными по абсолютной величине и направленными в противоположные стороны вдоль прямой,
соединяющей эти точки
 .
.
F12 - сила, действующая на первую материальную точку со стороны второй;
F21 - сила, действующая на вторую материальную точку со стороны первой.
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
Силы взаимодействия между материальными точками механической системы называются внутренними.
Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними.
Центр масс (или центр инерции) системы материальных точек (тел) есть некоторая точка в пространстве С, положение которой характеризует распределение масс системы.

закон движения центра масс
В случае отсутствия внешних сил:
Центр масс
замкнутой системы либо движется
прямолинейно и равномерно, либо остается
неподвижным.
![]()
Энергия, работа, мощность. Кинетическая энергия. Консервативные и неконсервативные силы, потенциальная энергия.
Энергия - универсальная мера различных форм движения и взаимодействия.
Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Элементарной работой силы F на перемещении dr называется скалярная величина:
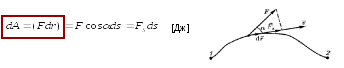
Мощностью,
развиваемой силой
 ,
называется скалярная физическая
величина, численно равная работе,
совершаемой этой силой за единицу
времени
,
называется скалярная физическая
величина, численно равная работе,
совершаемой этой силой за единицу
времени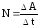 .Если в разные
моменты времени dt
совершаются разные работы, то используют
понятие мгновенной мощности
.Если в разные
моменты времени dt
совершаются разные работы, то используют
понятие мгновенной мощности
 .
.
Для движущихся тел можно получить формулу мгновенной мощности
 или
или  ,
,
т.е. мощность равна скалярному произведению векторов силы и скорости.
Чтобы охарактеризовать скорость совершения работы, вводят понятие
мощности:

Кинетическая энергия механической системы - энергия механического движения этой системы.
Работа силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела.

Консервативные
силы (потенциальные силы) – силы, работа
которых не зависит от формы траектории
(зависит только от начальной и конечной
точки приложения сил) . Характерное
свойство таких сил – работа на замкнутой
траектории равна нулю:
![]() К
консервативным силам относятся: сила
тяжести, гравитационная сила, сила
упругости и другие силы.
К
консервативным силам относятся: сила
тяжести, гравитационная сила, сила
упругости и другие силы.
Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
Потенциальная энергия - механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Закон сохранения импульса и энергии.
Закон сохранения энергии
Запишем второй закон Ньютона для n тел механической системы:


 Закон сохранения
энергии: в системе тел, между которыми
действуют только консервативные силы,
полная механическая энергия сохраняется,
т. е. не изменяется со временем.
Закон сохранения
энергии: в системе тел, между которыми
действуют только консервативные силы,
полная механическая энергия сохраняется,
т. е. не изменяется со временем.
Закон сохранения энергии (версия 2): в консервативных системах полная механическая энергия сохраняется.
Закон сохранения механической энергии связан с однородностью времени!
Угловая скорость и угловое ускорение. Момент силы и импульса механической системы. Закон сохранения момента импульса. Момент инерции твердого тела, теорема Штейнера.




Закон сохранения
момента импульса.



Принцип относительности Галилея. Преобразования Галилея и Лоренца. Постулаты теории относительности. Понятие одновременности.
