Задача интерполяции функции, интерполяционные полиномы:

Пусть на отрезке [a,b] задана функция ƒ(x). Задача интерполяции (или интерполирования) состоит в построении функции g(x), совпадающей с заданной ƒ(x) в некотором наборе точек {x₁,x₂,...,x_n+1} из отрезка [a,b] (эти точки называются узлами интерполяции), т.е. должны выполняться условия:

g(x_k)=y_k, k=1,2,...,n+1,

где y_k - известные значения функции ƒ(x) в точках x_k. Функция g(x) называется интерполянтом функции ƒ(x).

Построение интерполяционного полинома:

Для построения необходимо найти коэффициенты .

Для нахождения коэффициентов необходимо построить систему линейных уравнений, которая может быть получена на основании того, что многочлен проходит через все узловые точки.

.

В результате имеем систему:

Порядок системы равен . Параметры , известны и заданы в табличной функции. Неизвестными системы являются коэффициенты .

Интерполяционный многочлен по формуле Лагранжа имеет вид:

Многочлен является интерполяционным многочленом, т. е. в узловых точках он принимает значения таблицы.

Свернем формулу Лагранжа:

, где 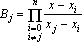. (Алгоритм метода Лагранжа не предусматривает получение многочлена в явном виде, а сразу находит значение в промежуточных точках.)

Построение интерполяционного многочлена по методу Ньютона

Пусть даны узлы –, а– значения функции или разделенные разности нулевого порядка. Тогда , – разделенные разности 1-го порядка; , – разделенные разности 2-го порядка. Разделенная разность -го порядка для-й точки вычисляется через разделенную разность -го порядка: . Лемма. Пусть произвольные попарно несовпадающие узлы, в которых известны значения функции. Тогда алгебраический многочлен-го порядка, который записывается в виде: является интерполяционным многочленом. Например, . Интерполяционный многочлен Ньютона Интерполяционный многочлен Ньютона используется для неравных промежутков.

19.)

. Полиномом Лагранжа называется полином n-й степени, проходящий через все точки . Если точки не образуют возвратов, то такой полином существует и является единственным. Под возвратом понимается ситуация, когда существуют две точки и такие, что .

Алгоритм построения полинома:

1.Полином строится как суммаполиномов n-й степени:

2.Каждый из полиномов , входящих в сумму, строится следующим образом. 3.Корнями полиномаявляются все точкиза исключением точки. 4.Единственностьобеспечивается за счет того, что коэффициент при старшем члене an подбирается так, чтобы полином проходил через точку. В записи Лагранжа полиномвыглядит следующим образом:

Линейная интерполяция состоит в том, что заданные точки (i=0. 1, ..., n) соединяются прямолинейными отрезками, и функция f(x)приближается ломаной с вершинами в данных точках.

Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется n интервалов , то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки и , в виде

 

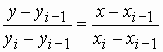
 Отсюда

, (1)

Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (1) и найти приближенное значение функции в этой точке.

Квадратичная интерполяция. В качестве интерполяционной функции на отрезке принимается квадратный трехчлен. Такую интерполяцию называют также параболической.

Уравнение квадратного трехчлена

, (2)

содержит три неизвестных коэффициента a_i, b_i, c_i, для определения которых необходимы три уравнения. Ими служат условия прохождения параболы (2) через три точки . Эти условия можно записать в виде

 (3)

При вычислении приближенного значения функции с помощью квадратичной интерполяции вместо формулы (1) нужно использовать (2) с учетом решения системы линейных уравнений (3). Интерполяция для любой точки проводится по трем ближайшим к ней узлам.

Пример. Найти приближенное значение функции y = f(x) при x = 0.32, если известна следующая таблица ее значений:

x	0.15	0.30	0.40	0.55
y	2.17	3.63	5.07	7.78

Воспользуемся сначала формулой линейной интерполяции (1). Значение x = 0.32 находится между узлами x_i-1= 0.30 и x_i = 0.40. В этом случае

,

,

.

Найдем теперь приближенное значение функции с помощью формулы квадратичной интерполяции (2). Составим систему уравнений (3) с учетом ближайших к точке x = 0.32 узлов: . Соответственно. Система (3.23) запишется в виде

Решая эту систему, находим . Искомое значение функции.

20.)

Схема Эйткена

Схема Эйткена предлагает более удобную форму нахождения полинома Лагранжа:  На первом этапе вычисляются многочлены L_0,1(x), L_1,2(x), :, L_n-1,n(x), построенные на каждой паре соседних узлов 0,1; 1,2; :; n-1,n соответственно.  При этом 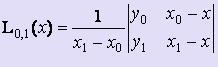, , :, .  Таким образом, многочлены, построенные на паре соседних узлов, вычисляются по формулам: .  Затем на основе этих многочленов вычисляются многочлены, построенные на тройках соседних узлов: .  И т.д. пока не получится один многочлен, построенный на всех узлах интерполяции: .  Полученный многочлен L_{0, 1, ..., n}(x) L_n(x).