Метод Гаусса – Зейделя

Расчетные формулы имеют вид:

т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.

Подробные формулы имеют вид:

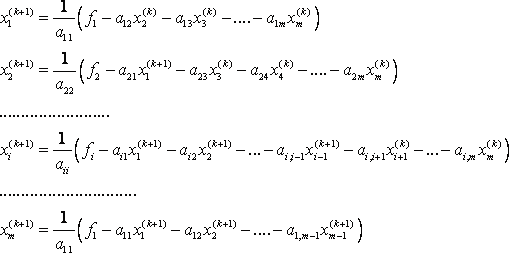
Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:

Алгоритм метода Зейделя

1. Преобразовать систему к виду одним из описанных способов.

2. Задать начальное приближение решения произвольно или положить , а также малое положительное число (точность). Положить .

3. Произвести расчеты по формуле (1)или (2) и найти .

(2)

(1)

4. Если выполнено условие окончания , процесс завершить и в качестве приближенного решения задачи принять . Иначе положить и перейти к пункту 3.

Достоинства итерационных методов:

1. Погрешность округления не накапливается от итерации к итерации.

2. Число итераций при n>100 обычно меньше n , поэтому общее число действий меньше n³, т.е. меньше, чем в методе исключений Гаусса.

3. Не требуется больший объем памяти.

4. Итерационные методы особенно выгодны для систем с большим количеством нулевых коэффициентов (систем с разряженной итерацией). Методы исключения наоборот: чем больше нулей, тем чаще требуется выбирать новую рабочую строку.

Недостаток - не всегда можно обеспечить сходность итерационного процесса. С увеличением размерности системы труднее выполнить линейные преобразования для обеспечения сходимости.

11.) Нормы векторов

Определение. Пусть имеется n - мерное метрическое пространство вещественных чисел . Если для любого вектора  существует число  такое, что: 1)    , причем ; 2)    , где aÎR; 3)    , - неравенство треугольника; то  называется нормой вектора X.

При решении СЛАУ наиболее распространены следующие нормы:

1. max-норма, или m – норма:     ;

2. l-норма:     ;

3. Евклидова норма:     .

Определение. Пусть X* – точное значение вектора, X ‑ приближенное значение. Абсолютная и относительная погрешность вектора X*:                    ,            .

Пример:

Вычислим нормы вектора 

1. m-норма: 

2. l-норма: 

3. Евклидова норма: 

12.) Нормы матриц

Согласованные с нормами векторов нормы матрицы A равны

1. max-норма, или m - норма:

;                (normi(A) в Mathcad)

2. l-норма:

;                 (norm1(A) в Mathcad)

3. Евклидова норма:

.                    (norme(A) в Mathcad)

Свойства норм матриц.

1)    , причем ;

2)    , где aÎR;

3)    ;

Дополнительно верны следующие свойства:

4)    ;

5)    , здесь X – вектор.

Как и для векторов, для матриц можно определить понятие погрешности.

Определение. Пусть A* – точное значение матрицы, A ‑ приближенное значение. Абсолютная и относительная погрешность матрицы A*:                    ,              .

Пример: Пусть

.

;

;

.

13.)

 Метод простых итераций, реализующийся в процессе последовательных приближений, сходится к единственному решению исходной системы при любом начальном приближении со скоростью не медленнее геометрической прогрессии, если какая-либо норма матрицы меньше единицы, т.е. .

1. Условие теоремы, как достаточное, предъявляет завышенные требования к матрице , и потому иногда сходимость будет, если даже.

2. Сходящийся процесс обладает свойством "самоисправляемости", т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, так как ошибочное приближение можно рассматривать, как новое начальное.

3. Условия сходимости выполняются, если в матрице диагональные элементы преобладают, т.е.

и хотя бы для одного неравенство строгое. Другими словами, модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов (свободные члены не рассматриваются).

4. Чем меньше величина нормы , тем быстрее сходимость метода.

Теорема о необходимом и достаточном условии сходимости метода простых итераций. Для сходимости метода простых итераций (10.12) при любых инеобходимо и достаточно, чтобы собственные значения матрицыбыли по модулю меньше единицы, т.е..

Преобразование системы к видус матрицей, удовлетворяющей условиям сходимости, может быть выполнено несколькими способами.Алгоритм:

1. Уравнения, входящие в систему , переставляются так, чтобы выполнялось условие преобладания диагональных элементов (для той же цели можно использовать другие элементарные преобразования). Затем первое уравнение разрешается относительно, второе — относительнои т.д. При этом получается матрицас нулевыми диагональными элементами.

Выражая из первого уравнения, — из второго, а — из третьего, получаем систему вида 

2. Уравнения преобразуются так, чтобы выполнялось условие преобладания диагональных элементов, но при этом коэффициенты не обязательно равнялись нулю.

3. Если , систему следует умножить на матрицу , где — матрица с малыми по модулю элементами. Тогда получается система или , которую можно записать в форме , где . Если достаточно малы, условие сходимости выполняется.

В ме­то­де простой ите­ра­ции если а_ii  0, то ис­ход­ная сис­тема мо­жет быть пре­об­ра­зо­вана к виду х_i = b_i + a_ij х_j , i  j, т.е. из каждого уравнения по­­сле­до­ва­тельно вы­ра­жа­ют х_i.

Здесь b_i = F_i / а_ii; a_ij = - а_ij / а_ii.

Таким образом, в мат­рич­ном виде имеем Х = В + AХ.

Полученную сис­­­­тему бу­дем решать методом по­сле­до­ва­тель­ных при­­ближений.

За ну­левое приближение Х⁽⁰⁾ мож­но при­нять матрицу В: Х⁽⁰⁾= = B, и далее, под­ста­вив най­денные значения в исходную систему, по­лу­чим Х ⁽¹⁾ = В + A Х⁽⁰⁾ .

При бесконечном повторении этой вы­чис­ли­тель­­ной схемы имеем

, гдеи будет искомое решение системы.

Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .

14.)

Итерационные методы решения линейных алгебраических систем:(основанны на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений.)Метод Гаусса – Зейделя

Расчетные формулы имеют вид:

т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.

Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

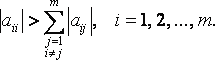
Начальное приближение: