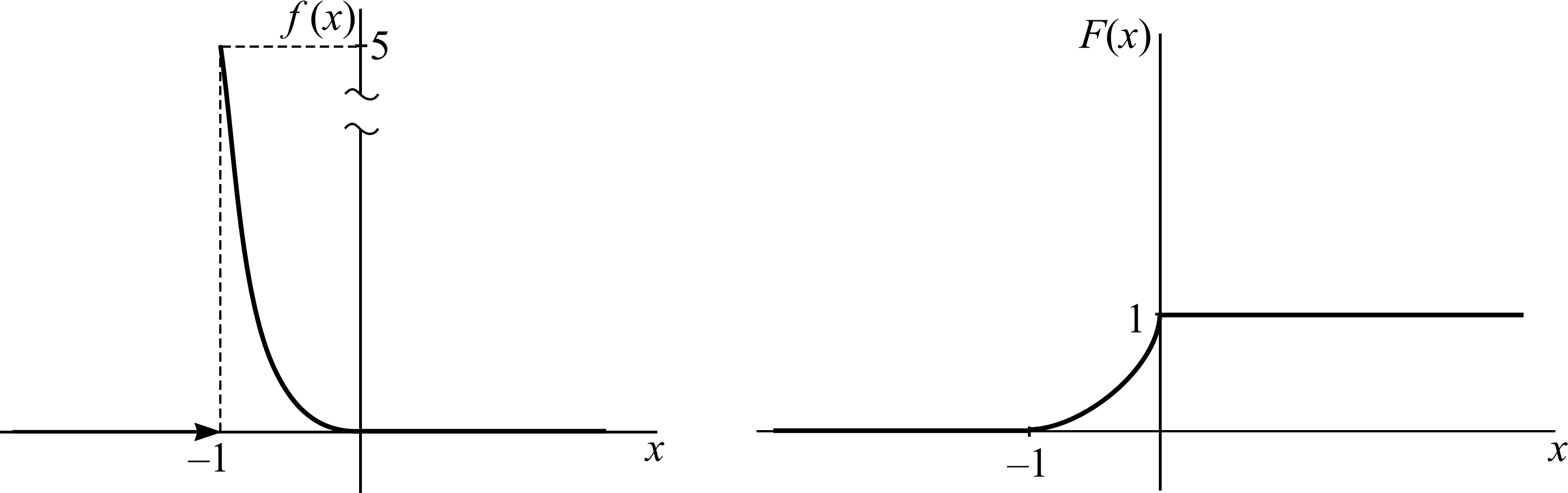Случайные величины

Пример 4.Дана корреляционная таблица случайного вектора (X,Y).

XY	–1	2
1	0,1	0,2
3	0,4	P22

Найти: P₂₂;F(2,2); ряды распределенияX,Y;P(X  1);P(1,5  X< 4);M[X];D[X];M[Y];D[Y];F(x); графикF(x) и многоугольник распределения; зависимыXиYили нет; коэффициент корреляцииr[x,y]; линию регрессииYпоX.

Из условия нормировки: 0,1 + 0,2 + 0,4 + P₂₂= 1,P₂₂= 0,3.

Значение функции распределения F(2,2) =P(X< 2;Y< 2) = 0,1.

Случайная величина Xпринимает значения 1; 3, причем

P(x = 1) = P(1; –1) + P(1; 2) = 0,1 + 0,2 = 0,3;

P(x = 3) = P(3; –1) + P(3; 2) = 0,4 + 0,3 = 0,7.

Ряд распределения X
X 1 3 Px 0,3 0,7	P(X  1) = P(1) = 0,3; P(1,5  X < 4) = P(3) = 0,7;

M[X] = 10,3 + 30,7 = 2,4;

D[X] =M[X²] – (M[X])²= (1  0,3 + 9  0,7) – 2,4²= 6,6 – 5,76 = 0,84.

Ряд распределения Y

Y	–1	2
Py	0,5	0,5

M[Y] = –1  0,5 + 2  0,5 = 0,5;

D[Y] = M[Y²] – (M[Y])² = 1  0,5 + 4  0,5 – 0,25 = 1,75.

Функция распределения F(x) =P(X<x):

F(x) = 0 приx1;

F(x) =P(1) = 0,3 при 1 <x3;

F(x) =P(1) +P(3) = 1 при 3 <x.

Окончательно:

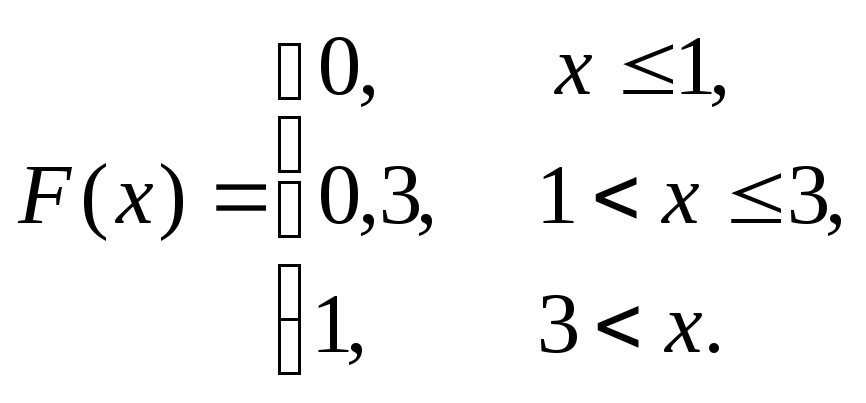
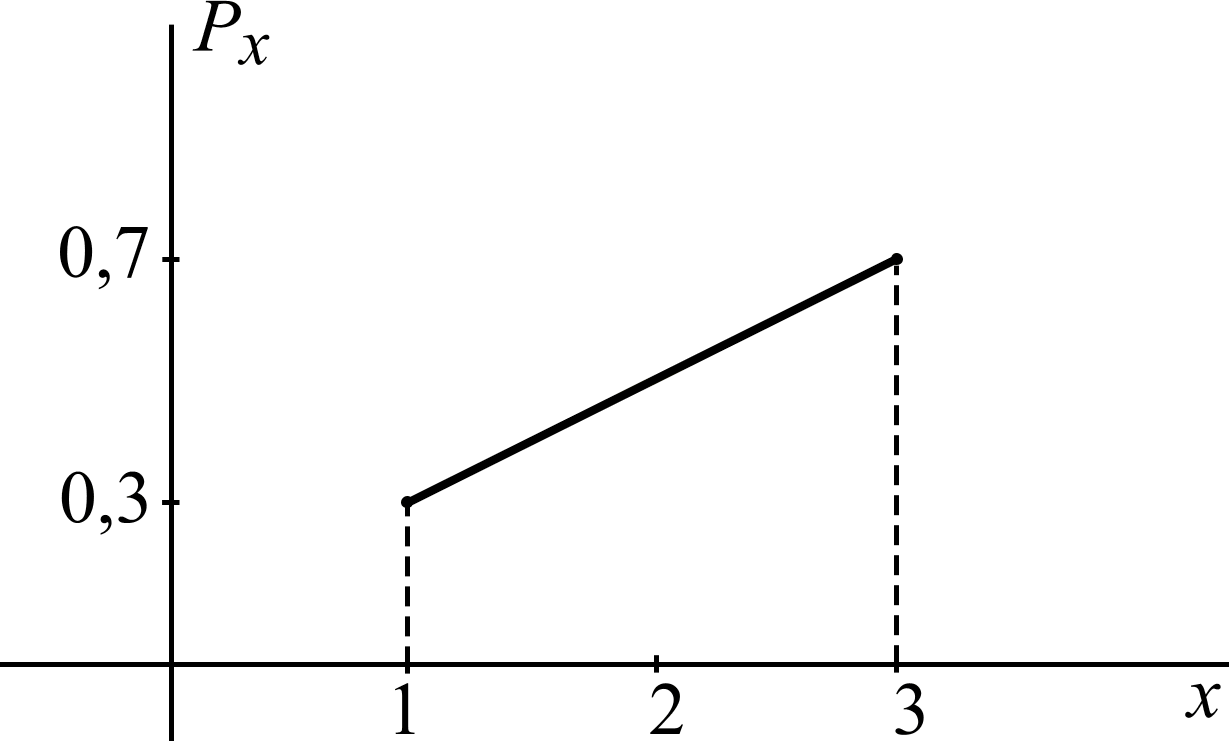
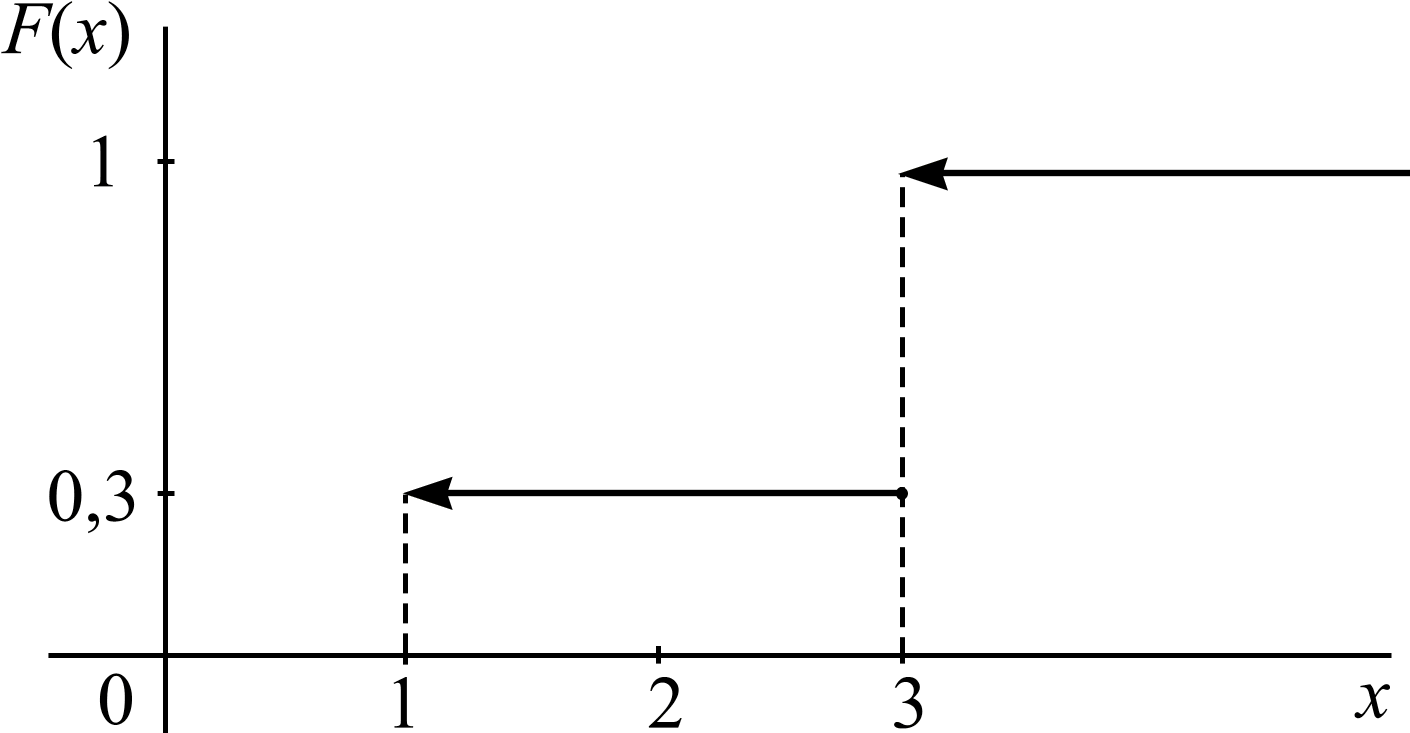
Изобразим многоугольник распределения (рис. 8) и график функции распределения F(x) (рис. 9).

Рис. 8	Рис. 9

Случайные величины XиYнезависимы, еслиP(X = x_i; Y = y_j) = = P(X = x_i)  P(Y = y_j).

Проверим для всех iиjэти равенства:

P(X = 1)  P(Y = –1) = 0,3  0,5 = 0,15; P(X = 1; Y = –1) = 0,1.

Равенство не выполнено, случайные величины XиYзависимы.

Найдем ;

K[X,Y] =M[XY] –M[X]M[Y] = 1  (–1)  0,1 +

+ 1  2  0,2 + 3  (–1)  0,4 + 3  2  0,3 – 2,4  0,5 = 0,9 – 1,2 = –0,3.

Найдем условные ряды распределения YпоX.
Y –1 2	Y –1 2

Найдем условные математические ожидания YпоX:

Нарисуем линию регрессии YпоX (рис. 10).

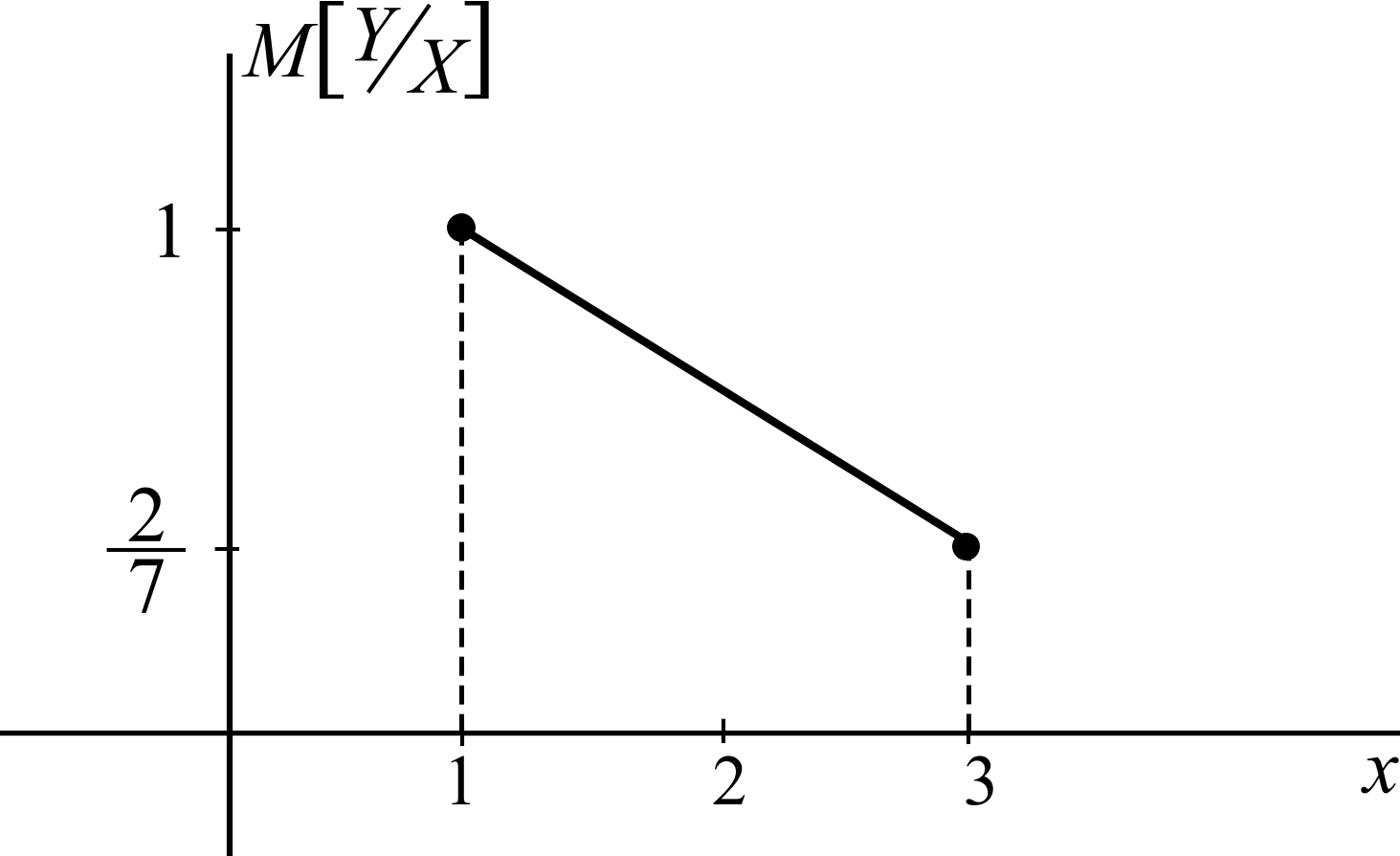
Рис. 10

Если r[X,Y] < 0, то зависимостьYотXубывающая, что видно из линии регрессии.

Пример 5.Дана функция распределения непрерывной случайной величиныX:

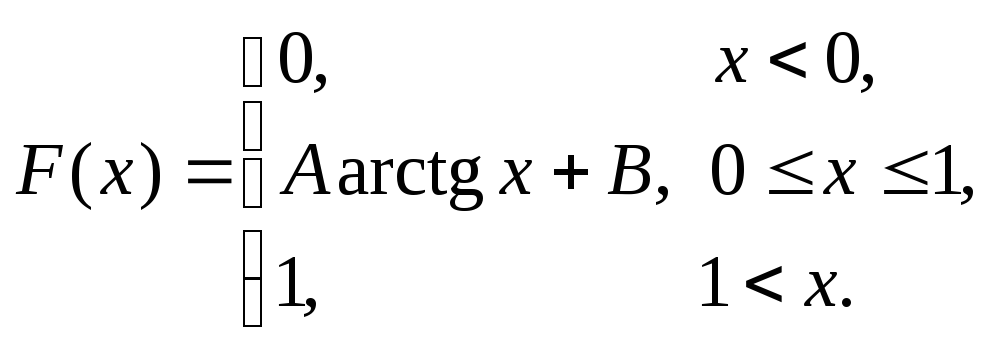
Найти: АиВ;M[X],D[X].

Для непрерывной случайной величины функция распределения непрерывна, поэтому

F(–0) = F(+0); F(1 – 0) = F(1 + 0);

0 = A arctg 0 + B; A arctg 1 + B = 1,

откуда 0 = В;следовательно,B = 0;;

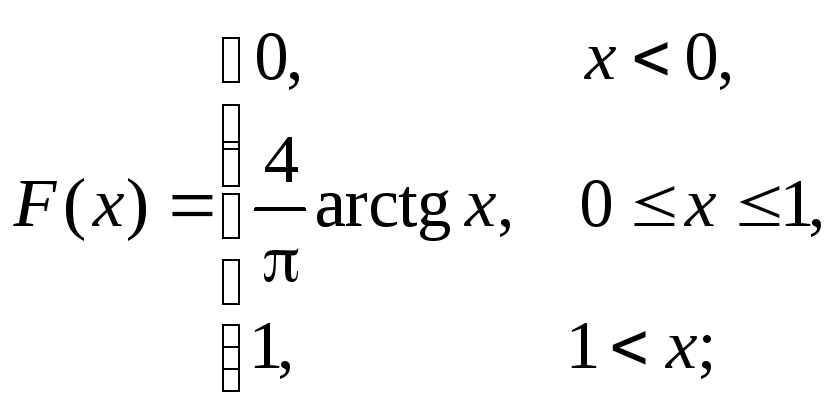
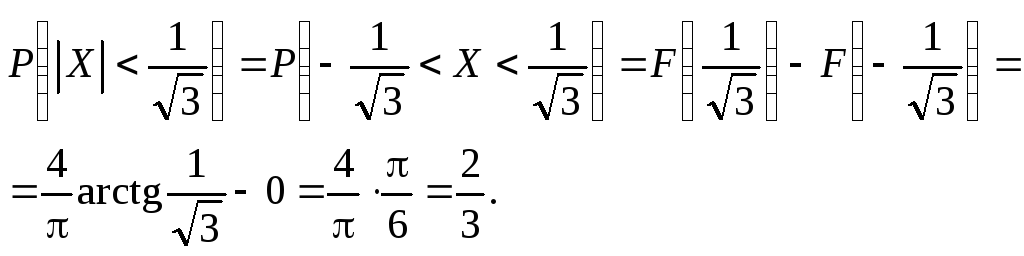
Найдем плотность распределения:

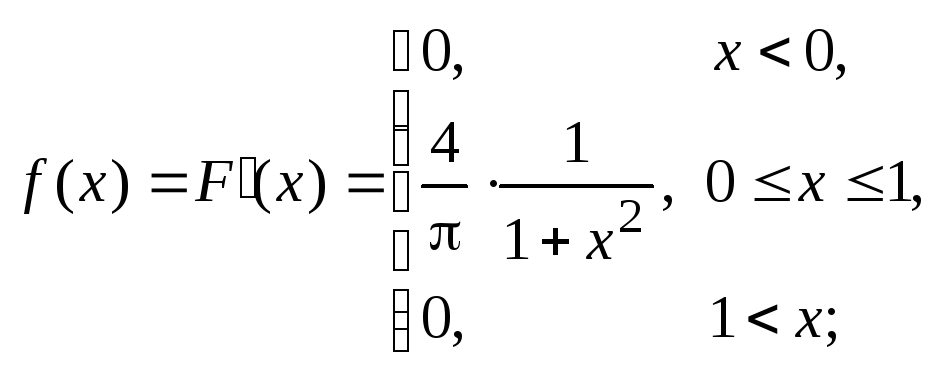
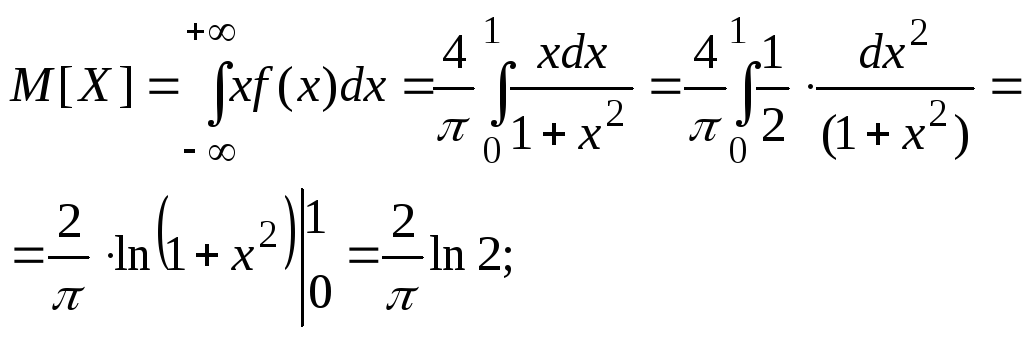
D[X] =M[X²] – (M[X])²;

поскольку

Пример 6.Дана плотность распределения непрерывной случайной величиныX:

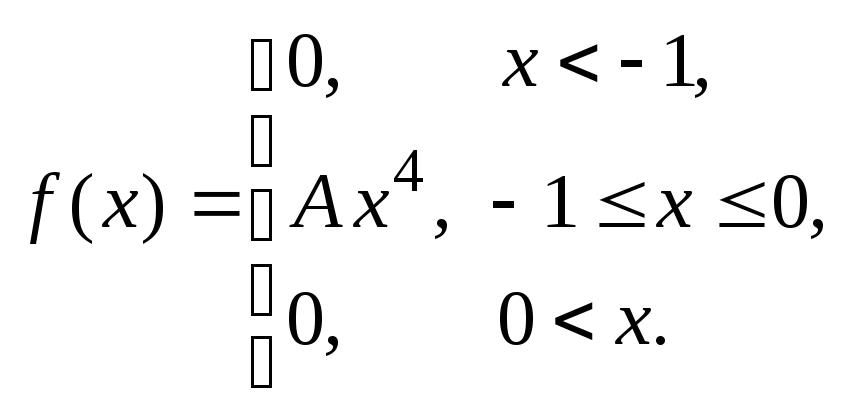
Найти: А,P(X> 0,5),F(x), графикиf(x) иF(x).

Из условия нормировки получаем:

Итак:

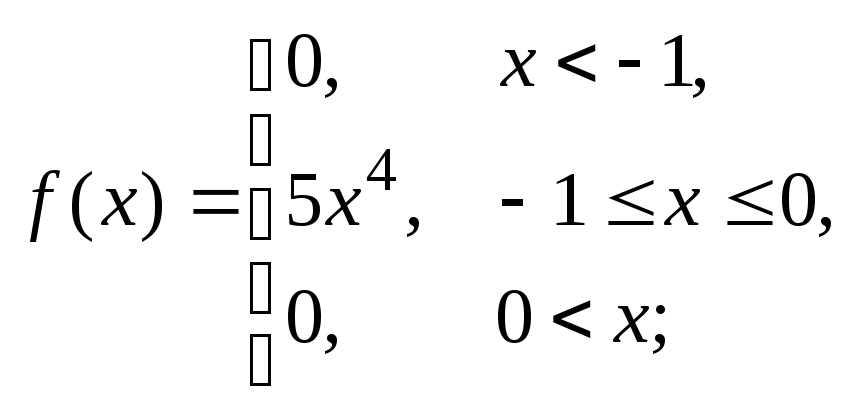
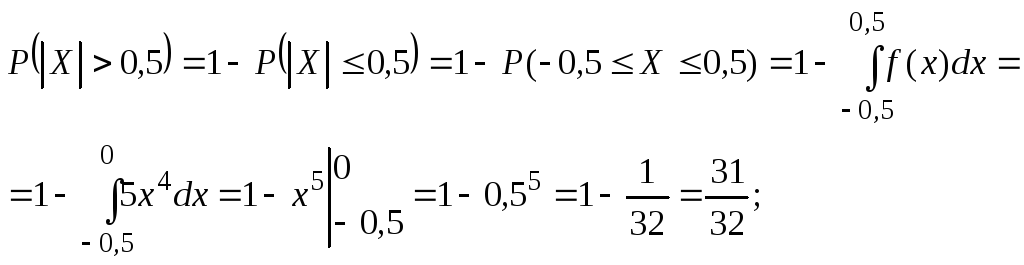
F(x) = 0 приx< –1;

при –1x0;

приx< 0.

Окончательно

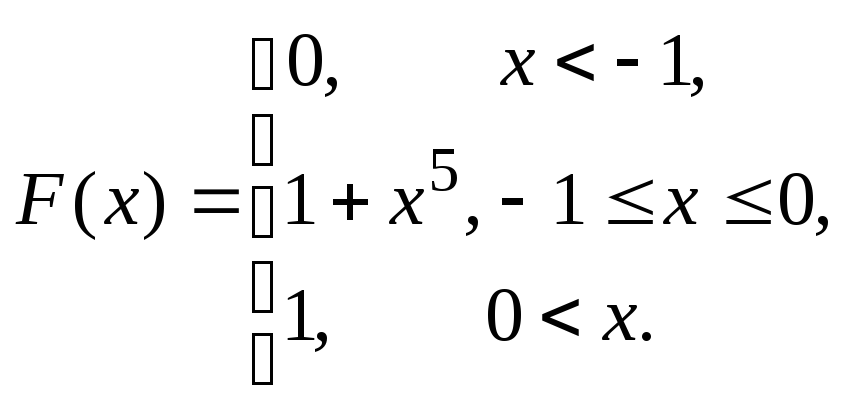
Графики f(x),F(x) представлены на рис. 11, 12.

Рис. 11	Рис. 12

Дискретная математика Программа дисциплины

1. Логические функции.

2. Свойства дизъюнкции, конъюнкции и отрицания.

3. ДНФ, СДНФ, КНФ, СКНФ.

4. Упрощение ДНФ. Карты Карно.

5. Полином Жегалкина.

6. Полные системы функций, базисы.

7. Элементы кодирования.