Решение типовых задач Случайные события

Пример 1.Найти надежность цепи, если надежности элементов указаны на схеме (рис. 6, 7).

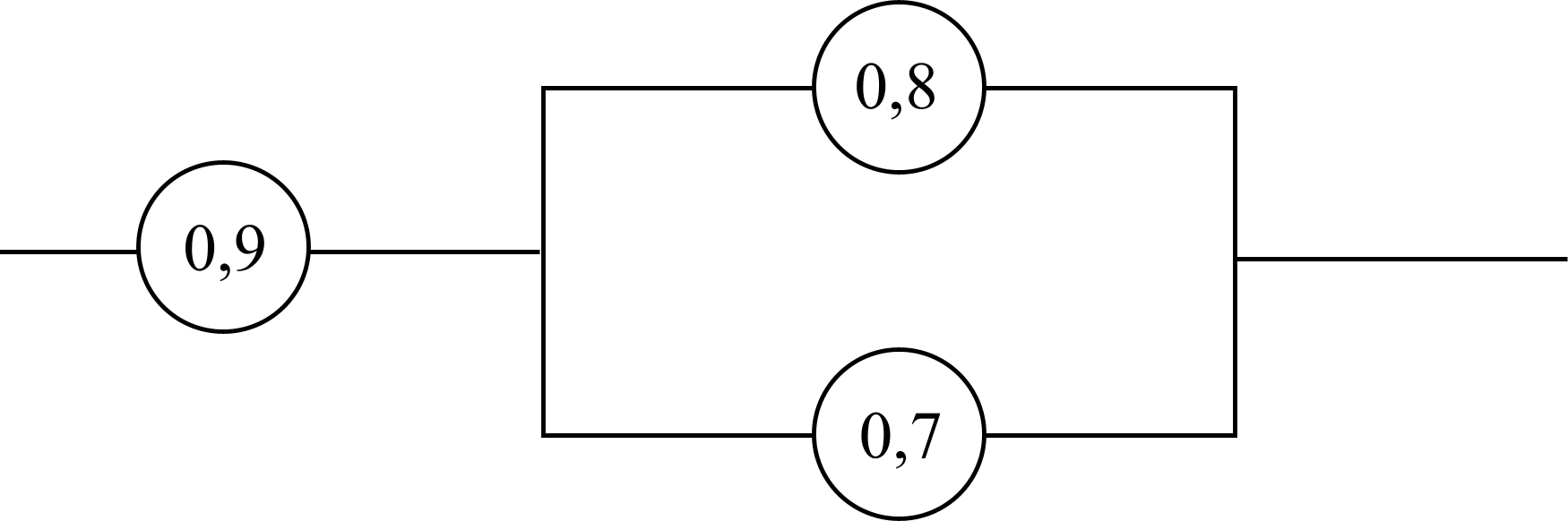
Рис. 6

Пусть событие Аналичие тока в цепи, гдеА₁,А₂,А₃– исправность элементов.

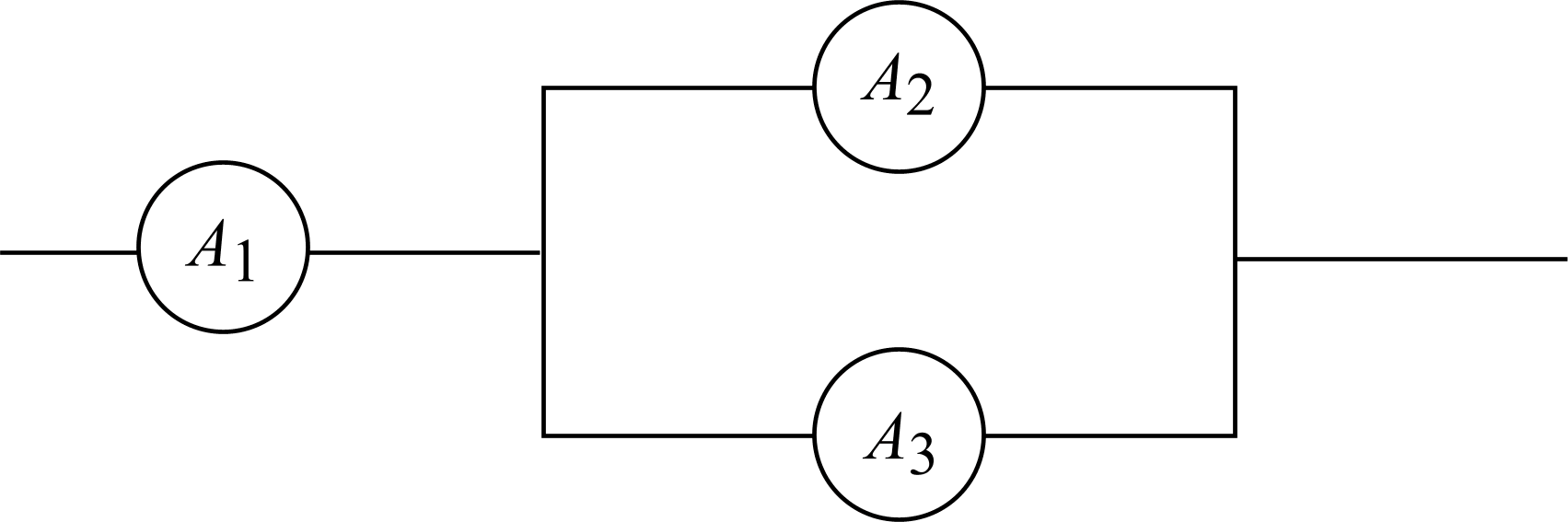
Рис. 7

Последовательному соединению отвечает произведение событий, а параллельному – сумма событий (сравните пример 10), поэтому имеем:

А=А₁(А₂+А₃).

Предполагается, что элементы работают независимо, следовательно, вероятность произведения событий равна произведению их вероятностей: P(A) =P(A₁)  P(A₂+A₃).

События A₂,A₃ совместны, следовательно,

P(A₂ + A₃) = P(A₂) + P(A₃) – P(A₂  A₃) = 0,8 + 0,7 – 0,8  0,7 = 0,94.

Этот результат можно получить иначе:

P(A₂ + A₃) = 1 – = 1 –=

= 1 – (1 – 0,8)(1 – 0,7) = 1 – 0,2 0,3 = 1 – 0,06 = 0,94.

Таким образом удобно находить вероятность суммы более чем двух совместных событий.

Окончательно P(A) = 0,90,94 = 0,846.

Пример 2. В группе студентов 2 отличника, 5 хорошо успевающих и 10 занимающихся слабо. Отличники на экзамене могут получить только отличные отметки; хорошие студенты с равной вероятностью хорошие и отличные; слабые студенты с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Вызываются наугад три студента. Найти вероятность того, что они получат отлично, хорошо и удовлетворительно.

Событие А– получение отличной, хорошей, удовлетворительной оценок, что возможно при одном из следующих условий (гипотез):

H₁ – вызваны 1 слабый, 1 хороший, 1 отличный студенты;

H₂ – вызваны 1 слабый и 2 хороших студентов;

H₃ – вызваны 2 слабых и 1 хороший студенты;

H₄ – вызваны 2 слабых и 1 отличный студенты.

Заметим, что гипотезы H₁,H₂,H₃,H₄не составляют полную группу, но при других условиях событиеА невозможно.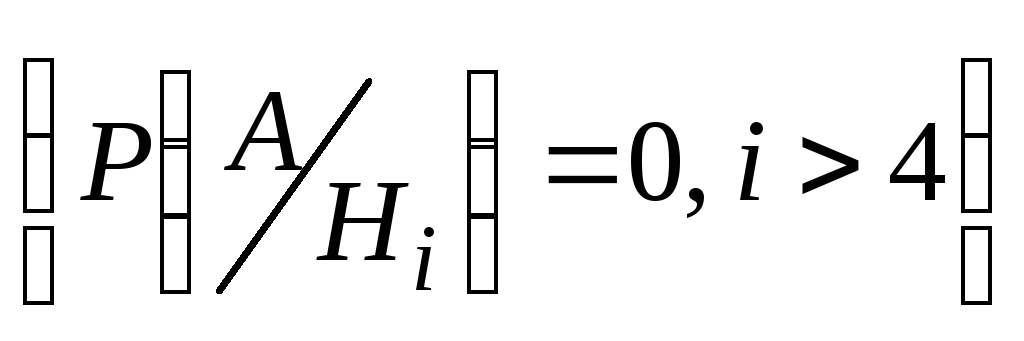

В тех случаях, когда наступление события Азависит от некоторых условий (гипотез), применяется формула полной вероятности:

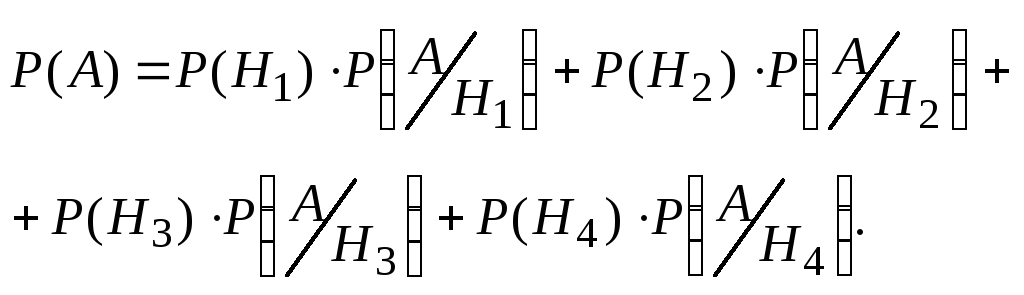
Найдем вероятности гипотез. Опыт состоит в выборе 3 студентов из группы 17 человек, следовательно, число всех исходов опыта:

В случае гипотезы H₁– это 1 студент из 10 слабых, 1 студент из 5 хороших и 1 из 2 отличных, значит, благоприятное число исходов

В случае H₂аналогично

Для H₃имеемдляH₄имеем

Окончательно, по формуле имеем:

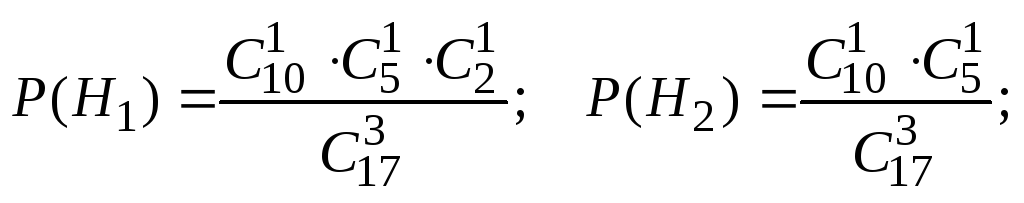
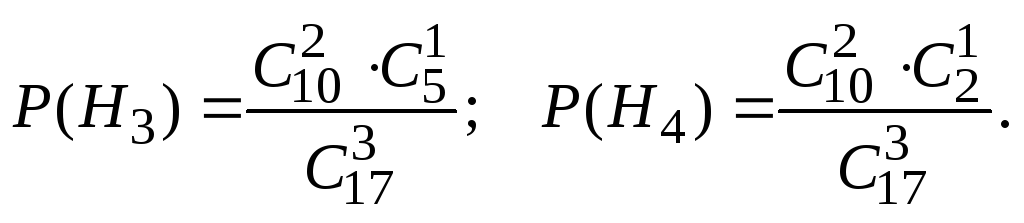
Найдем условные вероятности события при каждой гипотезе.

Событие – слабый студент получил удовлетворительную оценку (с вероятностью), хороший студент получил хорошую оценку (с вероятностью) и отличник получил отличную оценку (с вероятностью 1)

Событие – слабый студент получил удовлетворительную оценку (с вероятностью), хороший студент получил отличную, а другой – хорошую оценку (событиеD). Найдем вероятность последнего события.

Пусть В₁– отличную оценку получил первый хороший студент,

В₂– второй;

С₁– хорошую оценку получил первый хороший студент,

С₂– второй студент.

Тогда D = В₁С₂+В₂С₁.

События В₁С₂иВ₂С₁несовместны, поэтомуP(D) = P(В₁С₂) + P(В₂С₁).

События В₁,В₂,С₁,С₂независимы, окончательно:

P(D) =P(В₁)P(C₂) +P(В₂)P(C₁);

Событие – один слабый получил удовлетворительную, другой хорошую и хороший студент получил отличную оценки.

Аналогично предыдущему:

Событие – один слабый получил удовлетворительную, другой – хорошую, а отличник – отличную оценки.

Напомним, что 0! = 1;

Вычислим:

Пример 3.В группе из 10 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 – хорошо, 2 – посредственно, 1 – плохо. В билете 3 вопроса. Вероятность того, что отличник ответит на любой вопрос программы 0,9; для хорошего студента 0,7; посредственного 0,5; плохого – 0,2. Вызванный наугад студент ответил на 2 вопроса билета. Найти вероятность того, что он подготовлен хорошо.

Событие А– студент ответил на 2 из 3 вопросов билета; отвечавший мог быть отличником – гипотезаH₁, хорошим студентом –H₂, посредственным –H₃, плохим – H₄.

В отличие от предыдущего примера, событие Ауже произошло и надо найти вероятность того, что реализовалась вторая гипотеза, т. е. что отвечал хороший студент.

Для этого служит формула Байеса.

В нашем случае она имеет вид:

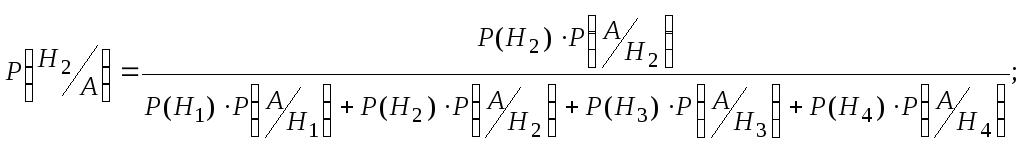
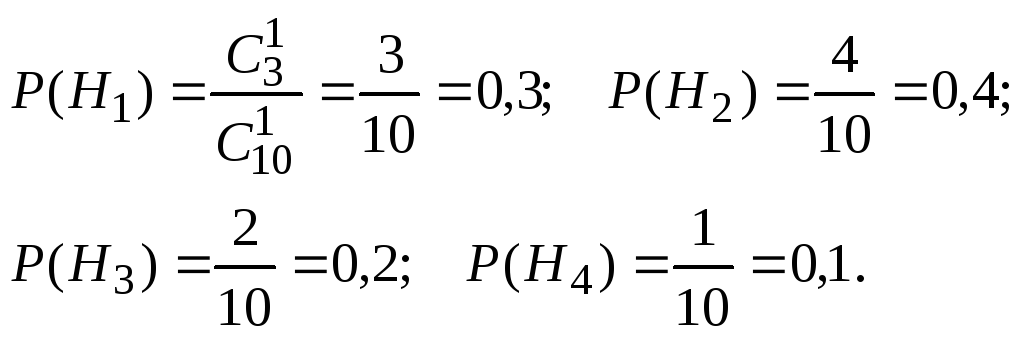
События H₁,H₂,H₃,H₄составляют полную группу.

Событие – студент ответил на 2 вопроса из 3, если вероятность ответить на любой вопросp= 0,9, а не ответитьq= 0,1.

Для нахождения используем формулу Бернулли:
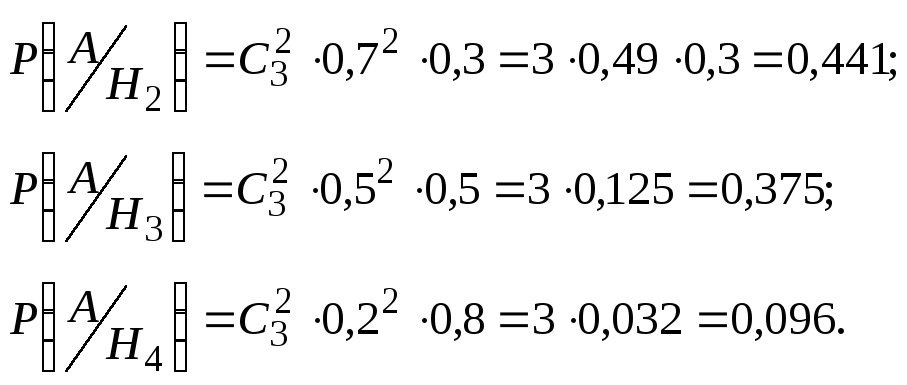